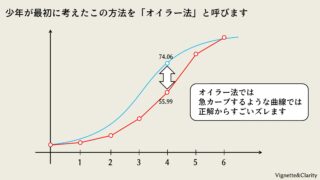
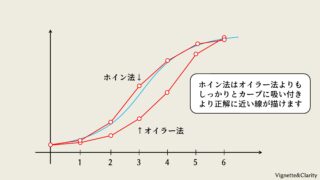
やること
5-1~5-3ではオイラー法とルンゲクッタ法の説明をしました。ここでは、ロトカボルテラの式を題材にしてオイラー法とルンゲクッタ法を比較してみます。
ロトカボルテラの式
ロトカボルテラの式は、捕食者と非捕食者の数の増減を表現した非線形微分方程式です。5-3ではキツネとオオカミの数として説明されています。
(1) 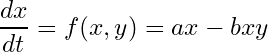
(2) 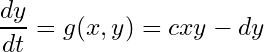
x がキツネの数で、(1)式はキツネの増減の勢いを表しています。y はオオカミの数で、式(2)はオオカミの増減の勢いを表しています。
a~d はパラメータで、正の値として説明します。ax はキツネが自身の数に応じて増えることを意味しており、a は例えば交尾の頻度のようなものです。-bxy はキツネとオオカミの数に応じてキツネが減ることを意味しており、xy はキツネとオオカミの出会いやすさ、b はキツネとオオカミが出会った場合の食べられる確率みたいなものです。
同様に考えると、cxy はオオカミがキツネを食べて増える項、-dy はオオカミが死んで自然に減ることを表しています。オオカミは交尾して増えないのか?という疑問は湧きますが、cxy に含まれていると考えましょう。
オイラー法
x, yの初期値やa~dのパラメータは先人がいい感じの値を見出してくれているので、有り難く使わせていただきます。シミュレーション時間は3秒間で、時間の刻み幅は0.01秒とします。
import numpy as np
import matplotlib.pyplot as plt
#初期値
x_ini = 10
y_ini = 7
#パラメータ
a = 8
b = 3
c = 4
d = 18
#シミュレーション時間
t_end = 3
#時間のきざみ幅
dt = 0.01
#傾きを求める式(非線形微分方程式)
def function(x, y):
dxdt = a*x - b*x*y
dydt = c*x*y -d*y
return [dxdt, dydt]
#時間配列timeを作成
time = np.arange(0, t_end, dt)
#x, yの配列を作成して初期値を入れる
x_set = []
y_set = []
x_set.append(x_ini)
y_set.append(y_ini)
#x, yに初期値をセット
x = x_ini
y = y_ini
#数値シミュレーション(オイラー法)
for t in time[1:]:
#傾きを求める
k1 = function(x, y)
#傾きをもとにx, yを更新
x = x + k1[0]*dt
y = y + k1[1]*dt
#x, yの値を配列に入れる
x_set.append(x)
y_set.append(y)
#グラフを表示
plt.plot(time, x_set, label='x')
plt.plot(time, y_set, label='y')
plt.xlabel('t')
plt.legend()
plt.show()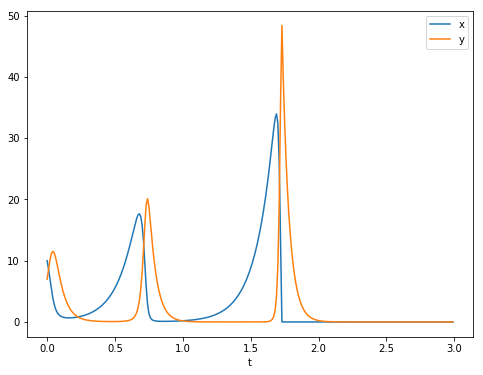
グラフを見ると、2秒時点でキツネ・オオカミともに絶滅してしまいました。
実はこれは正しくありません。非線形微分方程式の多くは解析的に解くことができないため、真のグラフは「神のみぞ知る」わけですが、とはいえオイラー法は誤差が大きく、真のグラフからかけ離れてしまうことが知られています。できれば後述のルンゲクッタ法で、より真に近い線を描きたいところです。
ルンゲクッタ法
ルンゲクッタ法では4つの傾きを計算し、これらを重み付けした傾きを採用してx, yを更新します。この方法だと、線がぐわんぐわん動くような微分方程式であっても、非常に高い精度で数値計算ができるとのことです。
#数値シミュレーション(ルンゲクッタ法)
for t in time[1:]:
#傾きを求める
k1 = function(x, y)
k2 = function(x + k1[0]*(dt/2), y + k1[1]*(dt/2))
k3 = function(x + k2[0]*(dt/2), y + k2[1]*(dt/2))
k4 = function(x + k3[0]*dt, y + k3[1]*dt)
#傾きをもとにx, yを更新
x = x + (1/6)*(k1[0] + 2*k2[0] + 2*k3[0] + k4[0])*dt
y = y + (1/6)*(k1[1] + 2*k2[1] + 2*k3[1] + k4[1])*dt
#x, yの値を配列に入れる
x_set.append(x)
y_set.append(y)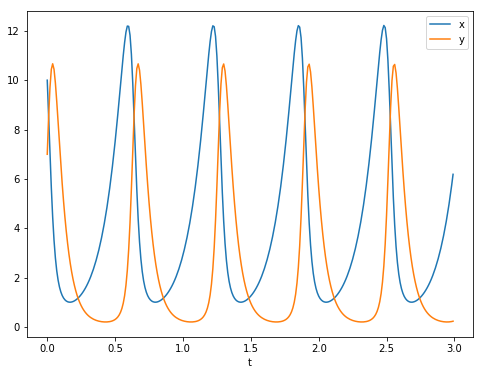
キツネとオオカミの数が振動しています。キツネが増えると、エサが増えるので少し遅れてオオカミが増えて、キツネは減少に転じます。キツネが減ると、少し遅れてオオカミも減り、またキツネが増えていきます。
odeintを使う方法
scipy.integrate.odeint を用いると、数値計算の実行部が1行で書けます。アルゴリズムは完全にルンゲクッタ法というわけではなく数式によって複数の手法を切り替えているようですが、十分な精度が期待できますので、こちらの方法でも良いでしょう。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
#初期値
x_ini = 10
y_ini = 7
#パラメータ
a = 8
b = 3
c = 4
d = 18
#シミュレーション時間
t_end = 3
#時間のきざみ幅
dt = 0.01
#傾きを求める式はこのように書く
def function2(v, t):
x = v[0]
y = v[1]
dxdt = a*x - b*x*y
dydt = c*x*y -d*y
return [dxdt, dydt]
#時間配列timeを作成
time = np.arange(0, t_end, dt, dtype=float)
#この1行で数値シミュレーション
v = odeint(function2, [x_ini, y_ini], time, args=())
#グラフを表示
plt.plot(time, v[:,0], label='x')
plt.plot(time, v[:,1], label='y')
plt.xlabel('t')
plt.legend()
plt.show()
先ほどのルンゲクッタと見分けがつきません。
結論
結局のところ真のグラフは「神のみぞ知る」ですが、現状は思考停止でルンゲクッタ使っておけばまあ文句は出ないので、数値計算(数値シミュレーション)をする際はルンゲクッタ法を用いましょう!