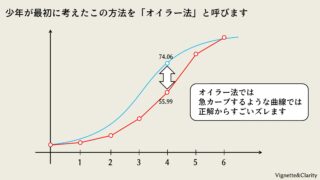
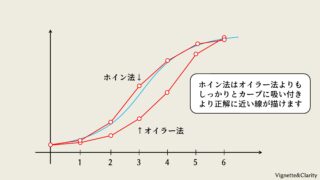
やること
1階の微分方程式のルンゲクッタ法については5-1~5-3で説明し、5-7で実装しました。
しかし、人工衛星の軌跡のシミュレーションでは加速度の式が与えられるため、2階の微分方程式のルンゲクッタ法をマスターしなければいけません。ここでは誤った実装と正しい実装を比較しながら学んでみます。
参考文献
2階の微分方程式のルンゲクッタ法の解説は数多くあれど、直接的に参考になったのはこちらです。感謝申し上げます!
重力プログラミング入門「第1回:地球の重力下で人工衛星を公転軌道に乗せる」
人工衛星の運動方程式
万有引力定数を G、地球の質量を M、衛星の質量を m、地球と衛星の距離を r と置くと、衛星が地球に引っ張られる力の大きさ F は次のとおりです。地球はでかいので (0, 0) で固定されているとします。
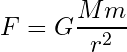
運動方程式より F = ma なので、衛星の加速度 a は地球に向かって、
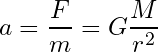
実装ではこれを (x成分, y成分) に分けて考えるので少しややこしいですが、頑張ります。
誤った実装
1階の微分方程式のルンゲクッタ法ではいわば速度の式が与えられ、4つの速度を加重平均して「採用する速度」とし、これで位置を更新しました。
これをそのまま次のように改造します。
2階の微分方程式ではいわば加速度の式が与えられ、4つの加速度を加重平均して「採用する加速度」とし、これで速度を更新する。そしてこれで位置を更新する。
これで次のような実装になります。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as pat
import math
#パラメータ
G = 10 #引力の強さ(適当)
M = 100 #地球の質量(適当)
m = 1 #衛星の質量(なんでもよい)
p_ini = [0, 10] #衛星の初期位置
v_ini = [8, 0] #衛星の初期速度
t_end = 3 #シミュレーション時間
dt = 0.01 #時間のきざみ幅
#運動方程式F=maから加速度a(2階の微分方程式)
"""
def function(x, y):
#衛星と地球の距離
r = ((0 - x)**2 + (0 - y)**2)**0.5
#衛星から地球への角度
theta = math.atan2(0 - y, 0 - x)
#引力の大きさ
F = G * M * m / r**2
#加速度aのx, y成分
ax = F / m * math.cos(theta)
ay = F / m * math.sin(theta)
return [ax, ay]
"""
#θを使わなくてもシンプルに書ける
def function(x, y):
#衛星と地球の距離
r = ((0 - x)**2 + (0 - y)**2)**0.5
#加速度aのx, y成分
ax = -G * M * x / r**3
ay = -G * M * y / r**3
return [ax, ay]
#時間配列timeを作成
time = np.arange(0, t_end, dt)
#x, yに初期値をセット
p = p_ini
v = v_ini
#位置の配列を作成して初期位置を入れる
ps = []
ps.append(p)
#数値シミュレーション(誤ったルンゲクッタ法)
for t in time[1:]:
#1つ目の傾き
k1 = function(p[0], p[1])
#2つ目の傾き
k2 = function(p[0] + k1[0]*(dt/2), p[1] + k1[1]*(dt/2))
#3つ目の傾き
k3 = function(p[0] + k2[0]*(dt/2), p[1] + k2[1]*(dt/2))
#4つ目の傾き
k4 = function(p[0] + k3[0]*dt, p[1] + k3[1]*dt)
#採用する傾き(加重平均)
k = [(k1[0] + 2*k2[0] + 2*k3[0] + k4[0])/6, (k1[1] + 2*k2[1] + 2*k3[1] + k4[1])/6]
#速度の更新
v = [v[0] + k[0]*dt, v[1] + k[1]*dt]
#位置の更新
p = [p[0] + v[0]*dt, p[1] + v[1]*dt]
#位置を記録
ps.append(p)
#グラフを表示
plt.figure(figsize=(8, 8))
ax = plt.axes()
#Earth
e = pat.Circle(xy=(0, 0), radius=1, color='k', alpha=0.3)
ax.add_patch(e)
#Satellite
ps = np.array(ps)
ax.plot(ps[:, 0], ps[:, 1], '-k', label='x')
#軸の設定
ax.set_aspect('equal')
ax.set_xlim(-15, 15)
ax.set_ylim(-15, 15)
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
plt.close()シミュレーション時間を変えて試してみると、
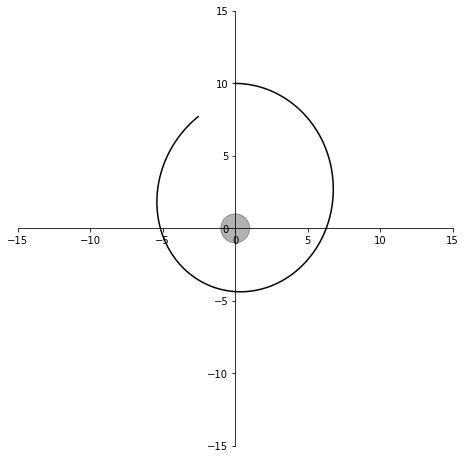
3秒間 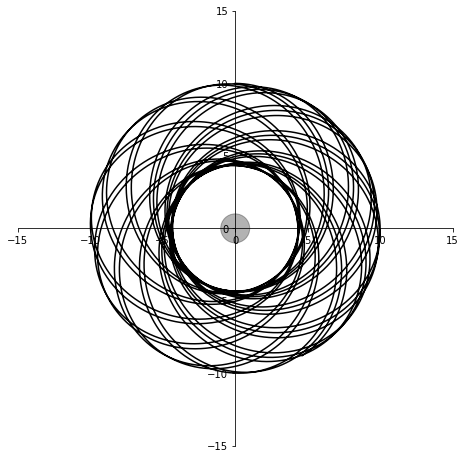
100秒間 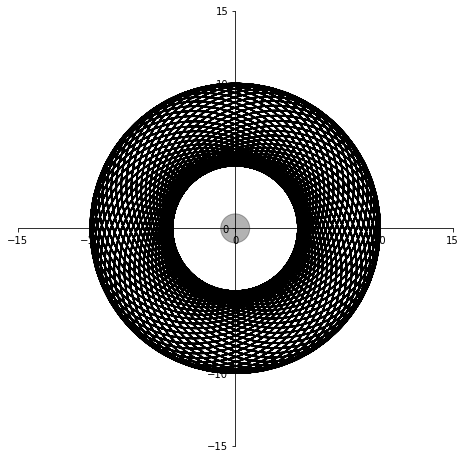
1000秒間
衛星の軌道はきれいな楕円になるはずですが、誤差のせいで歪んでいます。
正しい実装
該当部分を次のようにします。
4つの速度(k1~k4)と4つの加速度(l1~l4)を交互に求め、それぞれ加重平均して「採用する速度」「採用する加速度」とし、これらで位置と速度を更新する。交互に処理する上にx成分とy成分があるので、ややこしくてなかなか理解が進みませんでしたが、なんとか行けました。
#数値シミュレーション(正しいルンゲクッタ法)
for t in time[1:]:
#1つ目の傾き
k1 = [v[0], v[1]] #今の速度
l1 = function(p[0], p[1]) #今の加速度
#2つ目の傾き
k2 = [v[0] + l1[0]*(dt/2), v[1] + l1[1]*(dt/2)] #さっきの加速度を信じてdt/2進んだところの速度
l2 = function(p[0] + k1[0]*(dt/2), p[1] + k1[1]*(dt/2)) #さっきの速度を信じてdt/2進んだところの加速度
#3つ目の傾き
k3 = [v[0] + l2[0]*(dt/2), v[1] + l2[1]*(dt/2)] #さっきの加速度を信じてdt/2進んだところの速度
l3 = function(p[0] + k2[0]*(dt/2), p[1] + k2[1]*(dt/2)) #さっきの速度を信じてdt/2進んだところの加速度
#4つ目の傾き
k4 = [v[0] + l3[0]*dt, v[1] + l3[1]*dt] #さっきの加速度を信じてdt進んだところの速度
l4 = function(p[0] + k3[0]*dt, p[1] + k3[1]*dt) #さっきの速度を信じてdt進んだところの加速度
#採用する傾き(加重平均)
k = [(k1[0] + 2*k2[0] + 2*k3[0] + k4[0])/6, (k1[1] + 2*k2[1] + 2*k3[1] + k4[1])/6]
l = [(l1[0] + 2*l2[0] + 2*l3[0] + l4[0])/6, (l1[1] + 2*l2[1] + 2*l3[1] + l4[1])/6]
#位置と速度を更新
p = [p[0] + k[0]*dt, p[1] + k[1]*dt]
v = [v[0] + l[0]*dt, v[1] + l[1]*dt]
#位置を記録
ps.append(p)シミュレーション時間を変えて試してみても、
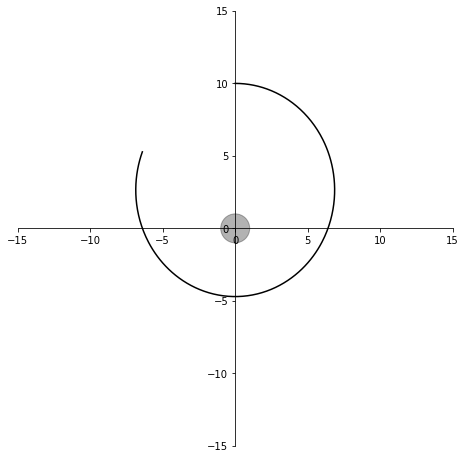
3秒間 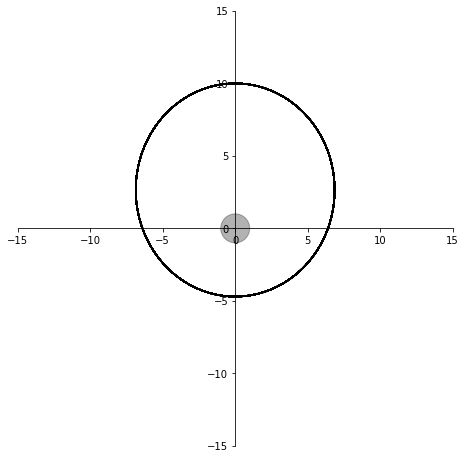
100秒間 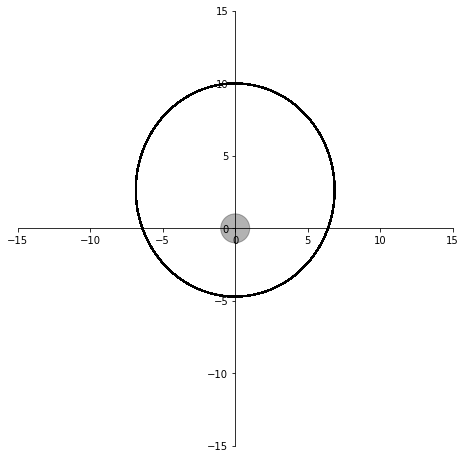
1000秒間
まったくズレる気配がありません!
スイングバイ
加速スイングバイ
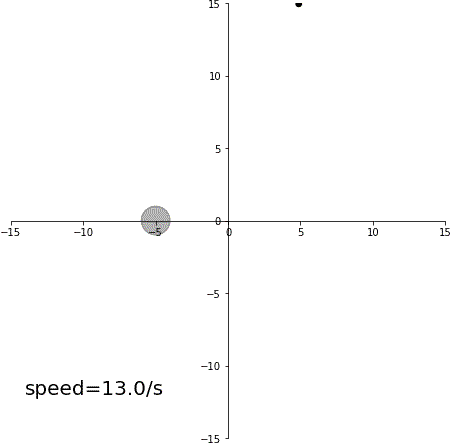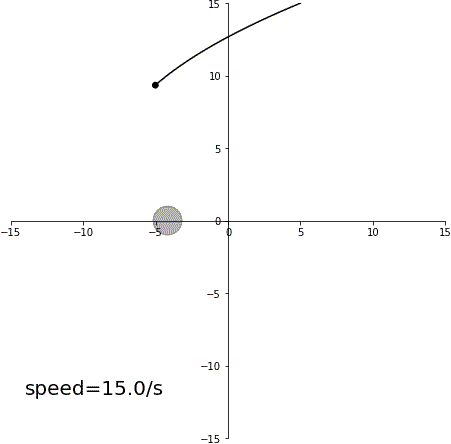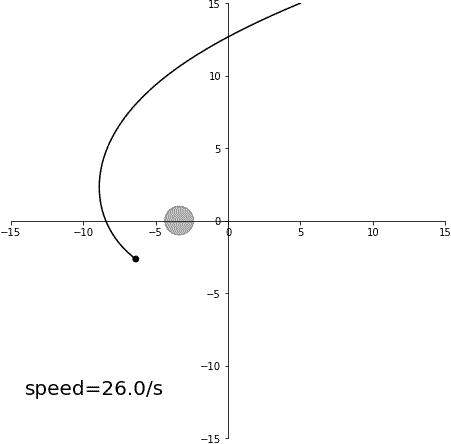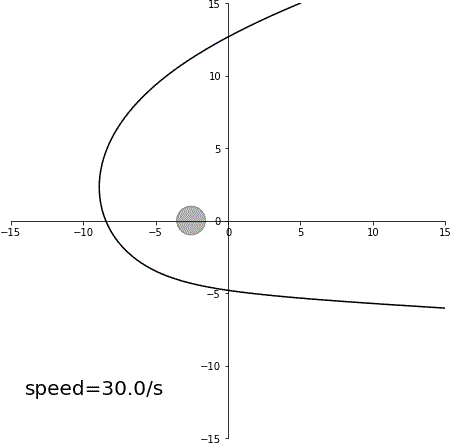
減速スイングバイ
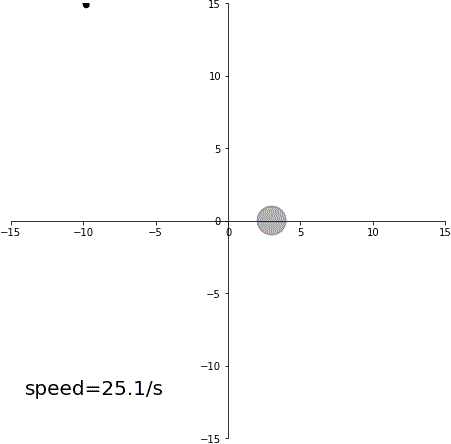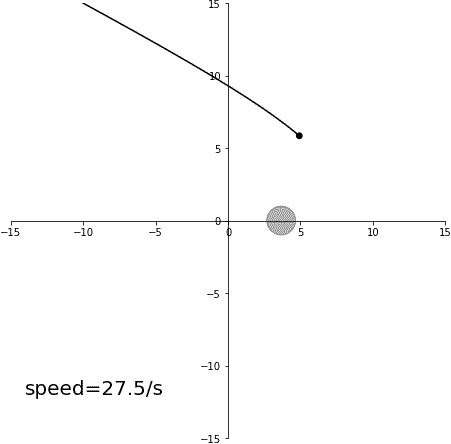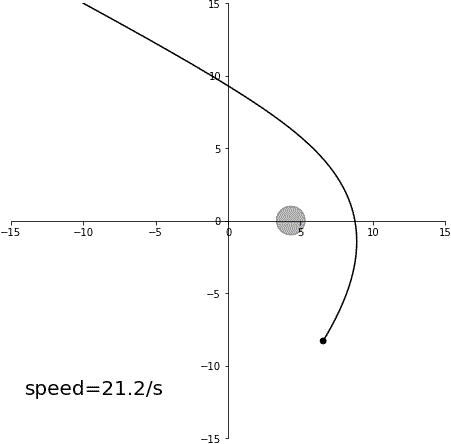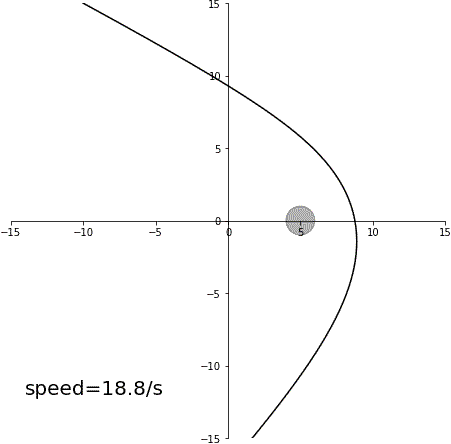
結論
スイングバイをリレーするようなコンセプトで、シューティングゲームかレースゲームを作ってみたいですね。