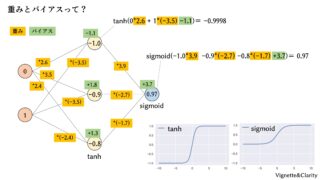
やること
ニューラルネットにおける「学習」とは、ニューラルネット中の重みとバイアスを最適化することにほかなりません。通常、ニューラルネットは誤差逆伝播法(バックプロパゲーション)というアルゴリズムで最適化します。しかし最適化といえばvcoptです。今回はvcoptでニューラルネットを学習してみます。
参考文献
Kerasを用いた深層学習の最小コードはこちらをご参照ください。
vcoptも頻繁にアップデートされています。
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
実行環境
Google Colaboratoryが利用可能です。

sin波の学習
sin波の学習において、誤差逆伝播法と遺伝的アルゴリズムを比較します。
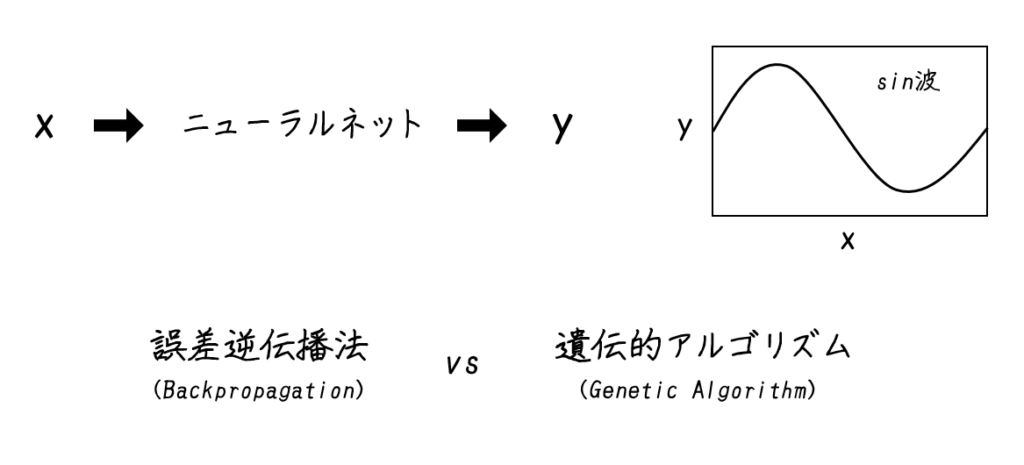
ニューラルネットモデル
5ユニットからなる中間層をひとつ置きます。重みは10個、バイアスは6個ありますので、全部で16パラメータの最適化です。これをKerasで手軽に学習します。
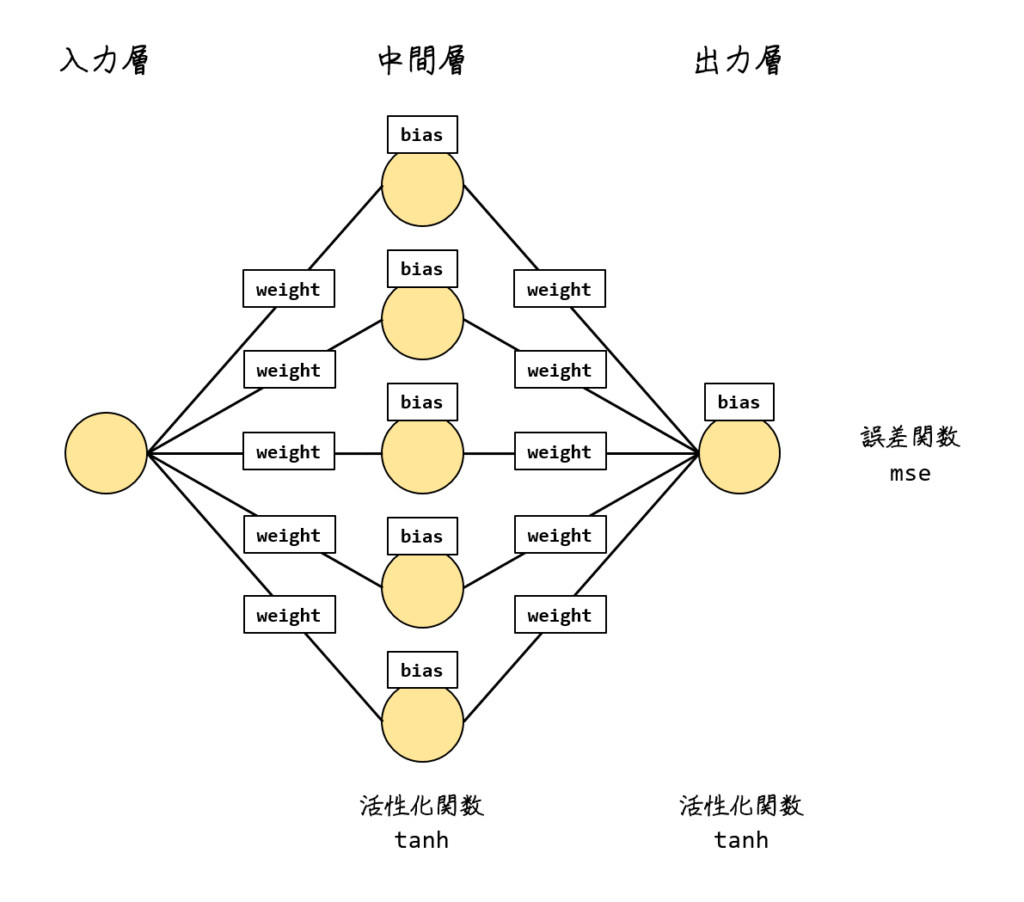
vcoptでも16パラメータの最適化を行います。各パラメータの対応は下の図のとおりです。

pipとimport
#Colabに初期装備されていないパッケージのインストール
!pip install vcopt#深層学習関連のimport
from keras.models import Sequential
from keras.layers.core import Dense
from keras.optimizers import Adam
from keras.callbacks import Callback
from sklearn.model_selection import train_test_split
#プロット関連のimport
import matplotlib.pyplot as plt
#GA関連のimport
from vcopt import vcopt
#その他のimport
import math
import numpy as np
import numpy.random as nr教師データの用意
教師データとなるx, yを用意します。yはノイズを加えてちょっとブレさせています。
#========================================================
#教師データの用意(sin波)
#========================================================
#乱数シードの固定
nr.seed(0)
#教師データの用意(sin波)
pi = math.pi
x, y = [], []
for i in np.arange(0, 2*pi, 0.02):
x.append(i)
y.append(math.sin(i) + nr.normal(0, 0.15))
x = np.array(x)
y = np.array(y)
#xは[0, 1]、yは[-0.8, 0.8]くらいに規格化
x = x / (2*pi)
y = y * 0.8
#教師データの数
print(len(x))
print(len(y))
#教師データの表示
plt.scatter(x, y, s=4, c='k')
plt.xlabel('x'); plt.ylabel('y'); plt.ylim([-1, 1]); plt.show()
#教師データを訓練データとテストデータに分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
#訓練データの表示
print(len(x_train))
print(len(y_train))
plt.scatter(x_train, y_train, s=4, c='b')
plt.xlabel('x'); plt.ylabel('y'); plt.ylim([-1, 1]); plt.show()
#テストデータの表示
print(len(x_test))
print(len(y_test))
plt.scatter(x_test, y_test, s=4, c='r')
plt.xlabel('x'); plt.ylabel('y'); plt.ylim([-1, 1]); plt.show()
教師データ
315訓練データ
220テストデータ
95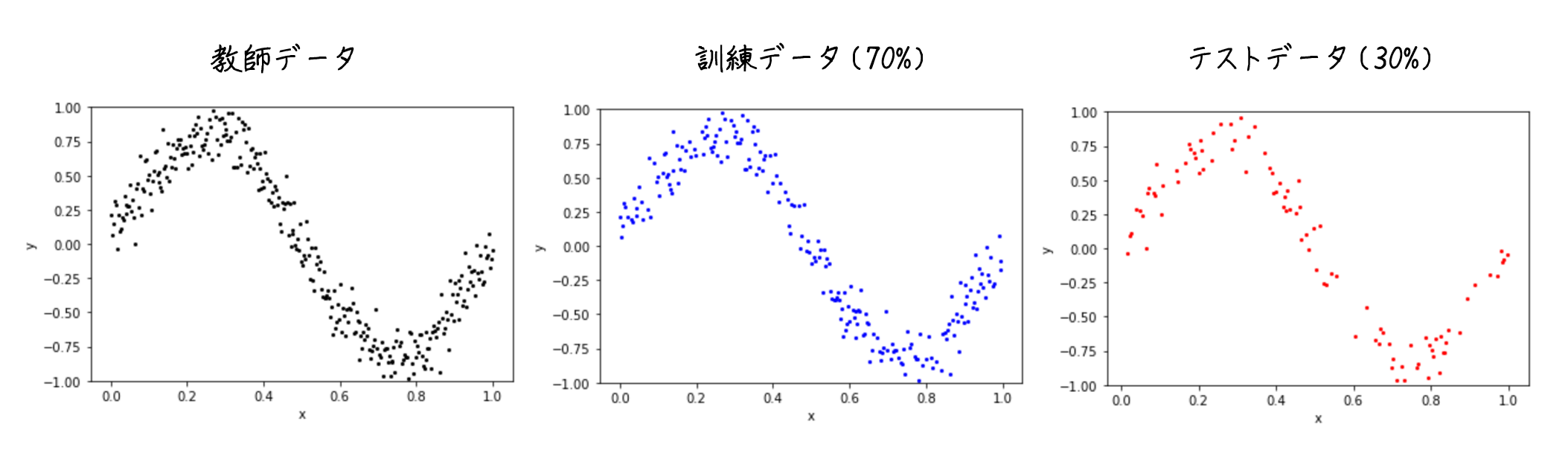
深層学習
Kerasはこんなに短いコードで深層学習ができます。
#========================================================
#深層学習
#========================================================
#ニューラルネットの用意
model = Sequential()
#入力値→中間層
model.add(Dense(5, input_dim=1, activation='tanh'))
#中間層→出力値
model.add(Dense(1, activation='tanh'))
#損失関数と最適化関数を指定してコンパイル
model.compile(loss='mse' , optimizer=Adam(lr=0.005))
#モデルの表示
model.summary()
#学習
hist = model.fit(x_train, y_train, validation_data=(x_test, y_test), batch_size=10, epochs=300)
#学習曲線の表示
plt.plot(hist.history['loss'], label='train')
plt.plot(hist.history['val_loss'], label='test')
plt.xlabel('epoch'); plt.ylabel('mse loss'); plt.legend(); plt.show()
#予測結果の表示
plt.scatter(x_test, y_test, s=3, c='r', label='test')
plt.scatter(x_test, model.predict(x_test), s=3, c='g', label='predict')
plt.xlabel('x'); plt.ylabel('y'); plt.legend(); plt.ylim([-1, 1]); plt.show()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_11 (Dense) (None, 5) 10
_________________________________________________________________
dense_12 (Dense) (None, 1) 6
=================================================================
Total params: 16
Trainable params: 16
Non-trainable params: 0
_________________________________________________________________
Train on 220 samples, validate on 95 samples
Epoch 1/300
220/220 [==============================] - 0s 2ms/step - loss: 0.2719 - val_loss: 0.2409
Epoch 2/300
220/220 [==============================] - 0s 356us/step - loss: 0.2205 - val_loss: 0.1964
・
・
・
Epoch 299/300
220/220 [==============================] - 0s 344us/step - loss: 0.0188 - val_loss: 0.0195
Epoch 300/300
220/220 [==============================] - 0s 329us/step - loss: 0.0185 - val_loss: 0.0194学習曲線
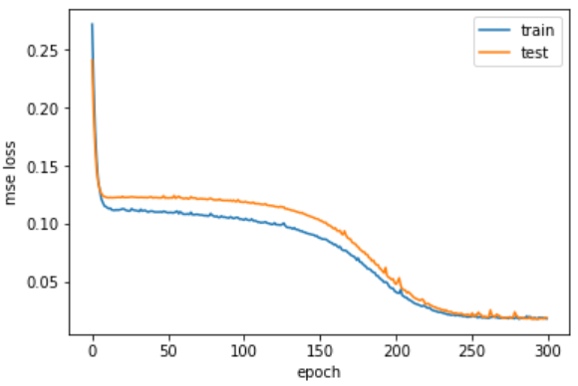
学習の様子
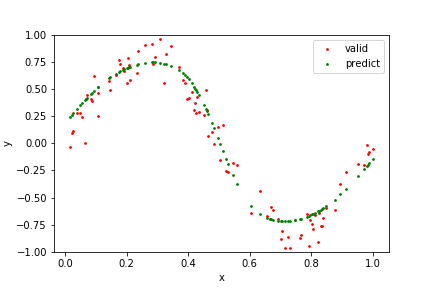
途中で勾配消失して停滞しますが、なんとか曲がりました。平均二乗誤差は訓練/テストともに0.018程度まで下がりました。
GA用のニューラルネット
ニューラルネットは自分で書くと理解が深まります。パラメータはきっちり16個使われます。
#========================================================
#GA用のニューラルネット(paraを重みとして、xからyを予測する)
#========================================================
def neural_vcopt(x, para):
#入力層(1ユニット)
now = x
#print('入力層\n{}'.format(now))
#入力層→中間層
#全結合(1ユニット→5ユニット)
weight = para[:5].reshape(1, 5)
now = np.sum(np.array([now]).T * np.array(weight), axis=0)
#バイアスを足す
bias = para[5:10]
now = now + bias
#活性化関数(tanh関数)
now = np.tanh(now)
#print('中間層\n{}'.format(now))
#中間層→出力層
#全結合(5ユニット→1ユニット)
weight = para[10:15].reshape(5, 1)
now = np.sum(np.array([now]).T * np.array(weight), axis=0)
#バイアスを足す
bias = para[15:16]
now = now + bias
#活性化関数(tanh関数)
now = np.tanh(now)
#print('出力層\n{}'.format(now))
return now[0]
#動作確認
x_tmp = nr.rand(1)
para_tmp = nr.rand(16) * 10 - 5
print(neural_vcopt(x_tmp, para_tmp))0.9999996061206216適当なxとparaを入れてやると、出力層の活性化関数がtanhなので、-1~1の結果が返ってきます。
評価関数
vcoptに渡す評価関数は、「訓練データのy」と「訓練データのxからニューラルネットで予測したy」のmse(平均二乗誤差)です。GAはこのmseが小さくなる方向に最適化を進めます。
#========================================================
#評価関数(paraを受け取って、220個の学習データをニューラルネットに通してyを予測し、平均二乗誤差を返す)
#========================================================
def sin_mse(para):
#二乗誤差を用意
mse = 0
#220個のx_trainをニューラルネットに通して、y_trainとの二乗誤差を計算
for i in range(len(x_train)):
#ニューラルネットでyを予測
y_tmp = neural_vcopt(x_train[i], para)
#y_trainとの二乗誤差
mse += (y_train[i] - y_tmp)**2
#平均二乗誤差を返す
return mse /len(x_train)
#動作確認
para_tmp = nr.rand(16) * 10 - 5
print(sin_mse(para_tmp))1.363385834467475適当なparaを入れてやると、適当なmseが返ってきます。
GAでニューラルネットの最適化
実数値の最適化を行うvcopt().rcGA()を実行します。para_rangeは[-5, 5]が16個並んだ2次元配列、評価関数はさきほどのsin_mse関数、目標値は0.0を渡します。show_pool_func=’print’はお手軽な表示法です。
#========================================================
#GAで最適化
#========================================================
#パラメータの初期範囲(16パラメータとも[-5, 5]の範囲)
para_range = np.ones((16, 2)) * 5
para_range[:, 0] *= -1
#print(para_range)
#GAで最適化
para, score = vcopt().rcGA(para_range,
sin_mse,
0.0,
show_pool_func='print',
pool_num=None)
print(para)
print(score)
#予測結果の表示
y_predict = []
for i in range(len(x_test)):
y_tmp = neural_vcopt(x_test[i], para)
y_predict.append(y_tmp)
plt.scatter(x_test, y_test, s=3, c='r', label='valid')
plt.scatter(x_test, y_predict, s=3, c='g', label='predict')
plt.xlabel('x'); plt.ylabel('y'); plt.legend(); plt.ylim([-1, 1]); plt.show()gen=0, best_score=0.152, mean_score=1.2456, mean_gap=1.2456, time=0.8
gen=160, best_score=0.1156, mean_score=0.9216, mean_gap=0.9216, time=2.36
・
・
・
gen=219840, best_score=0.0182, mean_score=0.0185, mean_gap=0.0185, time=2157.79
gen=220000, best_score=0.0182, mean_score=0.0185, mean_gap=0.0185, time=2159.35
・
・
・学習曲線
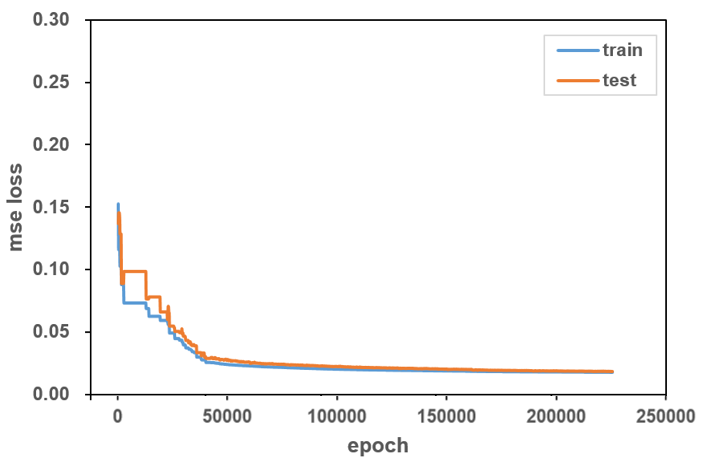
学習の様子
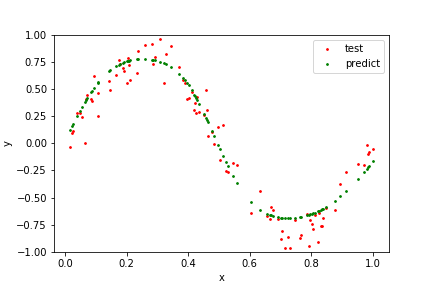
rcGA()はなかなか終わらないので途中で止めてしまいました。Kerasの方と同様に、平均二乗誤差は0.018程度まで下がりました。
途中の勾配消失のところでGAが終了してしまうこともあります。pool_numはデフォルトでは16の10倍で160個体ですので、pool_num=320といった感じで増やしても良いかもしれません。
感想
Kerasは20秒程度で終わりましたが、vcoptは10分以上かかりました。最適化にかかる時間を考えると、
各パラメータを数値微分して更新 >= GAによるパラメータ最適化 >> 誤差逆伝播法
かなと想像します。