やること
有名ゲームのマップを拝借してきました。
(よこ, たて)=(320, 256)で、11個の町があります。ここに半径60pxに電波が届く基地局を4つ置くとき、どこに置けば11個の町をカバーできるでしょうか?
今回は、遺伝的アルゴリズムで電波基地局をどこに置けばよいか最適化してみます。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
pip, import
vcoptをインストールします。
pip install vcopt今回用いるパッケージをインポートします。
#================================
# プロット関連のimport
#================================
import matplotlib.pyplot as plt
from PIL import Image, ImageDraw
#================================
# その他のimport
#================================
import numpy as np
import numpy.random as nr
from copy import deepcopy
#================================
# vcopt関連のimport
#================================
from vcopt import vcoptマップの読み込みと町の座標
マップを読み込んで、11個の町の座標をプロットしてみます。町の座標はがんばって探しました。
#================================
# マップの読み込みと町の座標
#================================
#マップの読み込み
img = Image.open('9-16_map.png').convert('RGB')
w, h = img.size
print('w, h\n{}, {}'.format(w, h))
#町の座標[よこ, たて]
town = np.array([[40, 40],
[88, 56],
[88, 136],
[88, 184],
[88, 248],
[168, 88],
[184, 216],
[216, 40],
[216, 88],
[216, 152],
[280, 88]])
#マップに町をプロット
img_tmp = deepcopy(img)
draw = ImageDraw.Draw(img_tmp)
for w_town, h_town in town:
draw.ellipse((w_town-2, h_town-2, w_town+2, h_town+2), fill=None, outline=(0, 0, 255))
#表示
plt.imshow(img_tmp)
plt.show()
plt.close()w, h
320, 256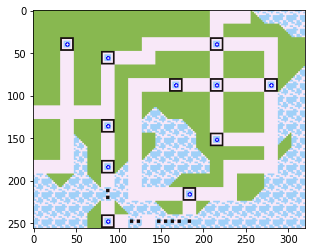
ちょっと分かりづらいですが、青い丸が町に重なっています。
評価関数
遺伝子設計
遺伝子配列(para)は、0.0~1.0の範囲を取りうる8つの数値とします。これがpara.shape=(4, 2)の2次元配列に変形され、4つの基地局の[よこ, たて]座標となります。「よこ」は320倍され0~320の整数に、「たて」は256倍され0~256の整数になり、この座標をそのままマップにプロットすることができます。
スコア設計
各町と各基地局の距離を計算し、各町が基地局にカバーされているかどうかのbool配列(covered)を算出します。coveredがすべてTrueであればスコア0.0を返します。そうでない場合は、カバーされていない町の中で一番離れている町が、カバー領域から何px離れているかを返します。要するにスコアが小さいほど「惜しい!」ことを意味します。
plotオプション
評価関数の2つ目の引数をTrueにすると、マップにカバー範囲がプロットされた図が出力されるようにしておきます。
#================================
# 評価関数
#================================
def score_func(para, plot=False):
#paraを基地局の座標に変形し[よこ, たて]、int形式にする
station = para.reshape((-1, 2))
station[:, 0] *= w
station[:, 1] *= h
station = np.array(station, dtype=int)
#print(station)
#plotオプションがTrueなら
if plot:
#マップに基地局をプロットして表示
img_tmp = deepcopy(img)
draw = ImageDraw.Draw(img_tmp)
for w_station, h_station in station:
draw.ellipse((w_station-2, h_station-2, w_station+2, h_station+2), fill=None, outline=(255, 0, 0))
draw.ellipse((w_station-60, h_station-60, w_station+60, h_station+60), fill=None, outline=(255, 0, 0))
#表示
plt.imshow(img_tmp)
plt.show()
plt.close()
#町と基地局の距離計算
dist = np.zeros((len(town), len(station)))
for i in range(len(town)):
for j in range(len(station)):
dist[i, j] = ((town[i, 0]-station[j, 0])**2 + (town[i, 1]-station[j, 1])**2)**0.5
#print(dist)
#各町がカバーされているかどうかのbool配列
dist_min = np.min(dist, axis=1)
covered = dist_min < 60
#print(covered)
#すべての町がカバーされていれば0を返す
if covered.all():
return 0.0
#カバーされていない町の中で一番離れている町が、カバー領域から何px離れているかを返す
short = np.max(dist_min[covered==False]) - 60
#print(short)
return short
para = nr.rand(8)
print(score_func(para, True))46.30145812734649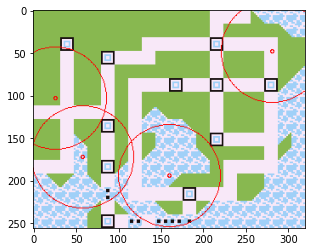
適当なparaを入力してplotオプションをTrueにしてみると、スコア46.3とマップが表示されました。電波があと46.3px伸びるとすべての町がカバーされることを意味します。
ちなみに基地局を20個にしてみると、すべての町がカバーされてスコア0.0になりました。
0.0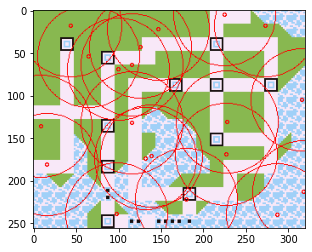
GAで最適化
パラメータ範囲は、各遺伝子が取りうる範囲である[0, 1]が8個並んだ2次元配列です。実数値の最適化ができるvcopt().rcGA()を用いて最適化します。
最適化後にscore_func(para, True)で基地局のカバー範囲を確認します。
#================================
# GAで最適化
#================================
#パラメータ範囲
para_range = np.zeros((8, 2))
para_range[:, 1] = 1
print(para_range)
#GAの実行
para, score = vcopt().rcGA(para_range, #パラメータ範囲
score_func, #評価関数
0.0, #目標値
show_pool_func='print') #GAの表示オプション
#結果の確認
score_func(para, True)[[0. 1.]
[0. 1.]
[0. 1.]
[0. 1.]
[0. 1.]
[0. 1.]
[0. 1.]
[0. 1.]]
________________________________________ info ________________________________________
para_range : n=8
score_func : <class 'function'>
aim : ==0.0
show_pool_func : 'print'
seed : None
pool_num : 80
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 80/80
gen= 0, best_score= 44.202, mean_score= 105.313, mean_gap= 105.313, time= 0.3
gen= 80, best_score= 29.828, mean_score= 71.940, mean_gap= 71.940, time= 0.3
gen= 160, best_score= 24.172, mean_score= 55.019, mean_gap= 55.019, time= 0.4
gen= 240, best_score= 22.735, mean_score= 47.177, mean_gap= 47.177, time= 0.4
.
.
.
gen= 1440, best_score= 2.514, mean_score= 15.169, mean_gap= 15.169, time= 1.1
gen= 1520, best_score= 2.514, mean_score= 13.015, mean_gap= 13.015, time= 1.1
gen= 1600, best_score= 2.201, mean_score= 12.337, mean_gap= 12.337, time= 1.1
gen= 1680, best_score= 0.000, mean_score= 11.213, mean_gap= 11.213, time= 1.2
_______________________________________ result _______________________________________
para = np.array([0.69395761, 0.36384209, 0.29488698, 0.80931686, 0.19961001, 0.34821509,
0.59593233, 0.69551337])
score = 0.0
________________________________________ end _________________________________________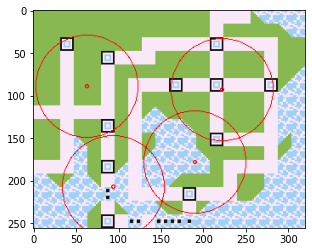
はい、数秒で最適化できました。
もしかして3基地局でも?
もしかしてと思い、3基地局でやってみました。パラメータ範囲を書き換えるだけです。
#パラメータ範囲
para_range = np.zeros((6, 2))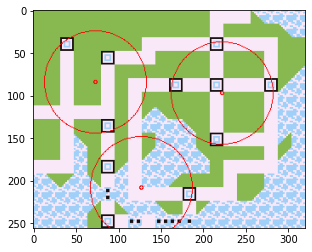
できました。
もしかして2基地局でも?
・・・
_______________________________________ result _______________________________________
para = np.array([0.657996, 0.52753749, 0.20164155, 0.56406479])
score = 46.733312513010674
________________________________________ end _________________________________________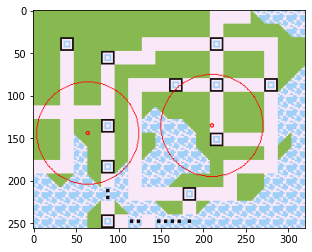
さすがに無理でした。しかしながら、もっとも電波の弱い2つの町の基地局までの距離が等しくなるような設計になっていますので、妥協案としては上出来ではないでしょうか。