やること
ビリヤードでは基本的に小さい数字の的球から順番にポケットしていきます。このとき、次の的球を狙いやすい位置に手球を意図的に誘導するテクニックをポジショニングと言います。
例えばこのような感じです。
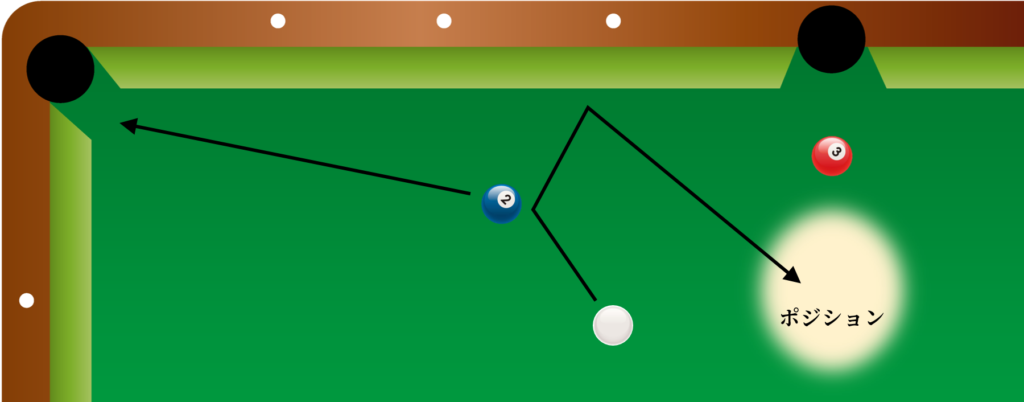
このポジショニングゾーンの形状やサイズはどんなものか、プレーヤーなら一度は気になったことがあるでしょう。ショットの際、手玉はキューが指す方向に射出されますが、技量によっては多少左右にブレるでしょう。このブレる最大角を θ [°]とします。初心者は θ が大きく、プロは θ が小さいと考えられます。
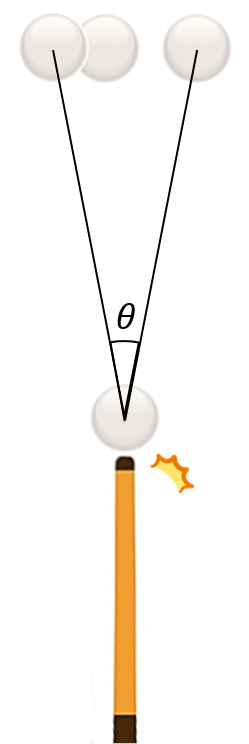
ここでは、ブレる最大角 θ [°]によってポジショニングゾーンの形状とサイズがどう変化するか、理論的に考察してみましょう。
イマジナリーボールの許容幅
ポケットの幅を 2w、ポケットから的球までの距離を l、的球の半径を r とします。ポケットに入れるためのイマジナリーボールは点線のように描け、この許容幅を 2a とします。まずは a をこれらの変数で表してみます。
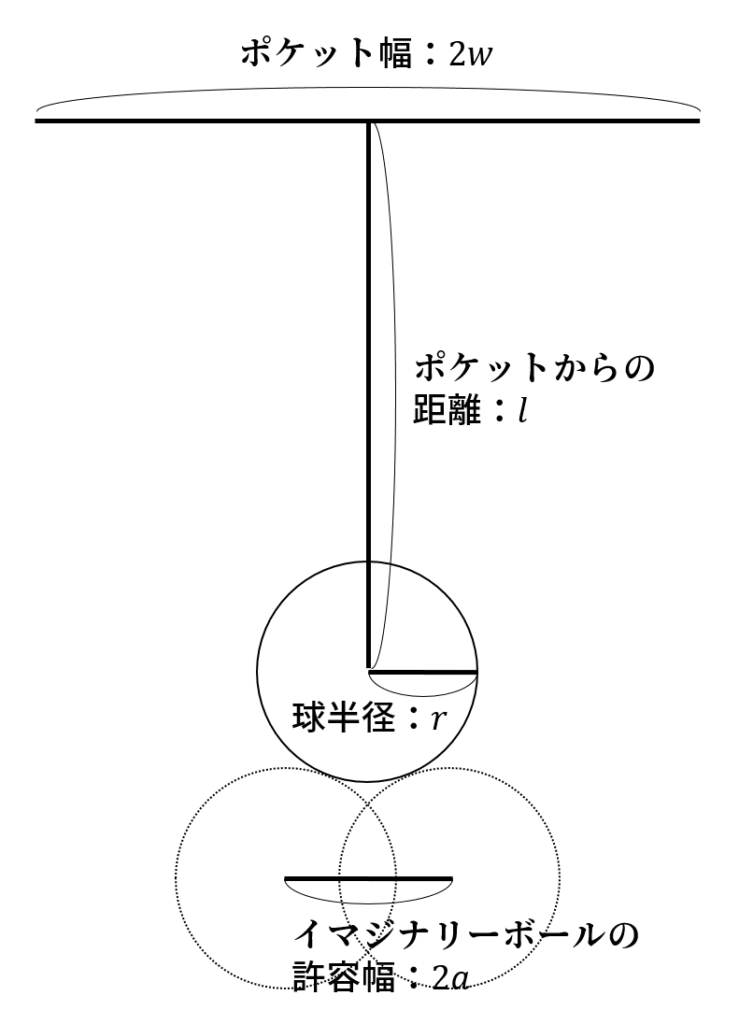
補助線を入れました。
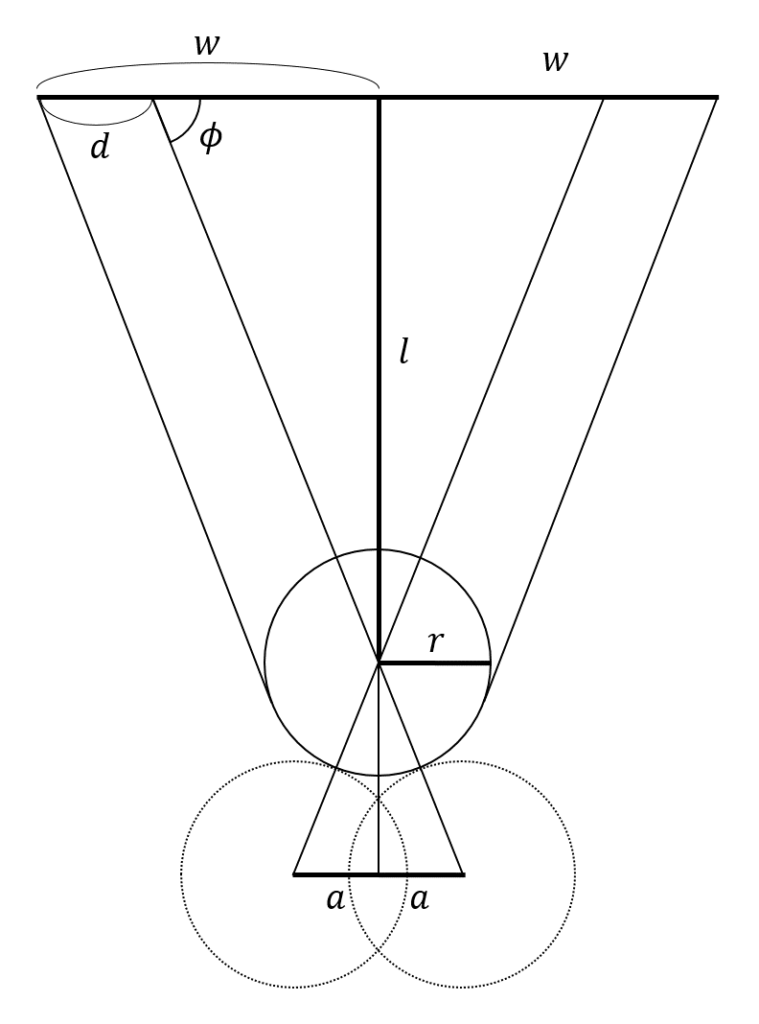
計算過程は省略しますが、w << l のため a ≒ d といった近似を用いてがんばると、
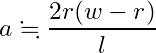
と表せました。
ポジショニングゾーンの形状とサイズ
次に、手玉がブレ角 θ で射出されるとして、イマジナリーボールの許容幅 2a に収まるような手玉の範囲(ゾーン)を考えます。このゾーンの形状と半径 R(円なのか?)はどんなものでしょうか。
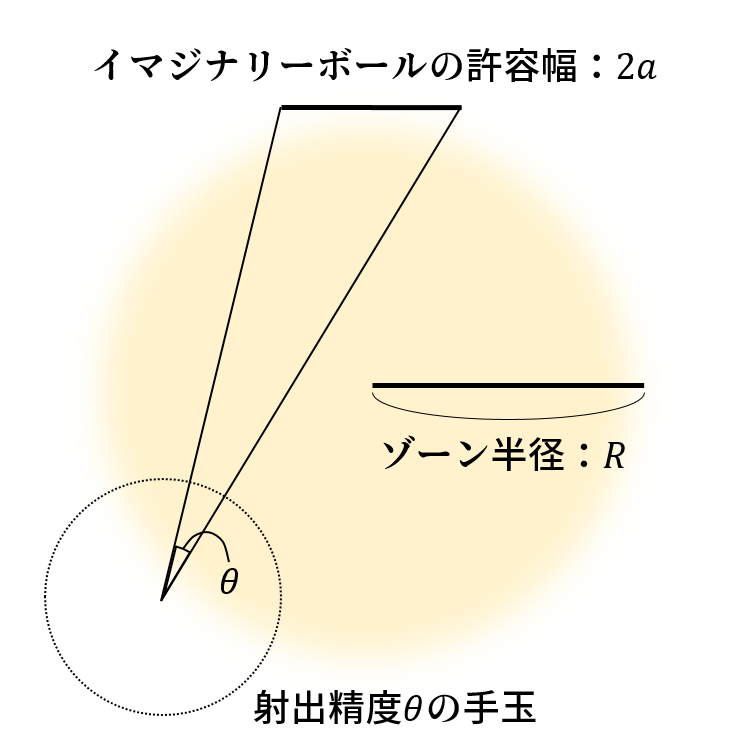
補助線を入れました。
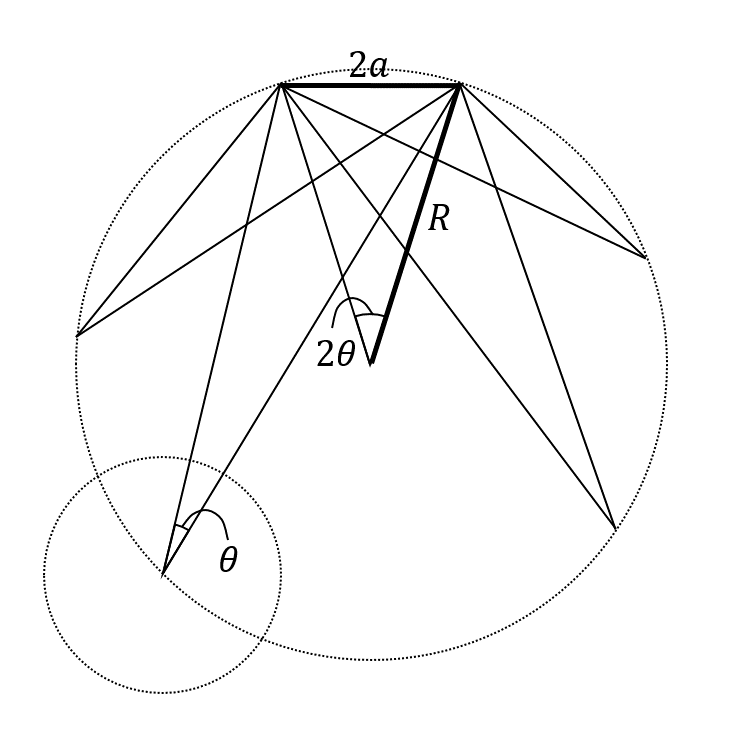
ここで面白いことに気が付きます。円周角の定理により、ゾーンの形状は円形であることが分かりました。円周上でショットした場合には、最大でブレたときにイマジナリーボール許容幅いっぱいにギリギリ収まります。円内からのショットであればいくぶん余裕があります。
このゾーンの半径 R は、
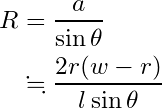
となりました。
ここでビリヤードの実際のポケット幅と球半径を代入してみます。ポケット幅は約12cm、球の直径は5.72cm、またポケットから的球までの距離は30cmとします。
![]()
ブレる最大角 θ [°]に応じたポジショニングゾーンを描画しました。
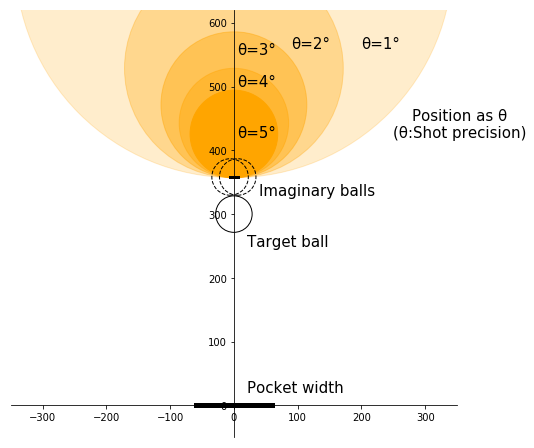
θ = 1° の腕前があればポジショニングゾーンは広いですが、初心者で θ = 5° までブレ得る場合にはとても狭いです。(それ以前にゾーンに持ってこられないですが・・・)
ポケットから的球までの距離を60cmにした場合はこちらです。

θ = 1° の腕前があってもゾーンは狭く見えます。θ = 0.5° 程度までショットの精度を上げるべきでしょう。これがスヌーカーの長距離ポケットともなればさらに桁違いのショット精度が要求されるでしょう。皆さんは Ronnie O’Sullivan おじさんを知っていますか?
結論
ポジショニングゾーンは円形で、その半径は的球がポケットから離れるほど、またショットの精度が悪いほど小さくなる。