21-14. 量子アニーリング（QUBO）で橋をかけろ（Bridges）を解く

量子コンピュータ

2023/05/04

やること
おさらい
どうやって橋をかけろを解くのか
コード
さいごに

やること

QUBOでパズルを解くのがちょっと楽しくて、今回は橋をかけろ（リンクブリッジ）を解いてみたいと思います。

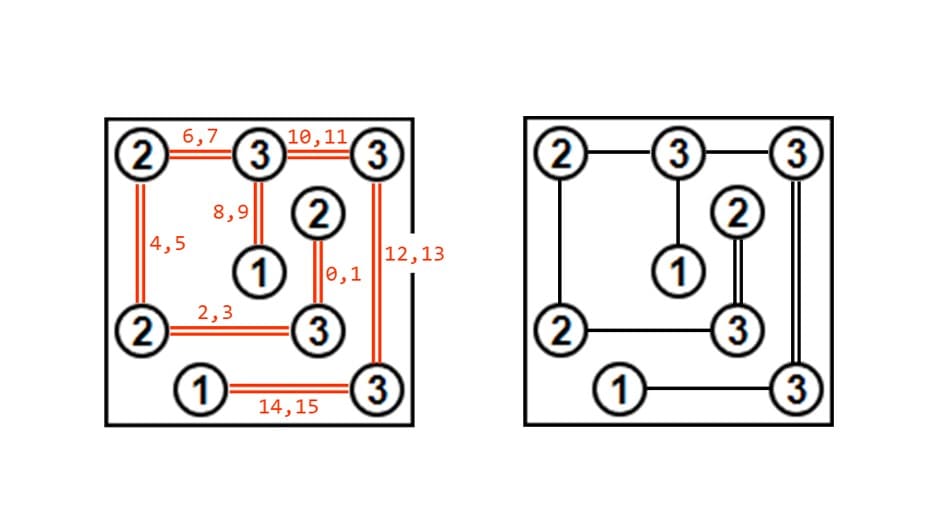
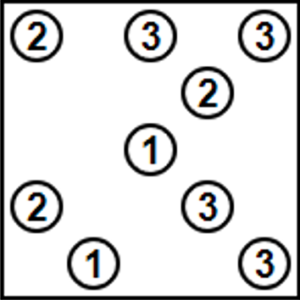
問題がこちら

答えがこちらです。

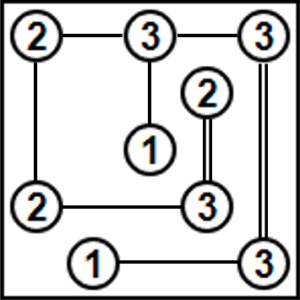
各数字から、数字の個数だけ上下左右に橋をかけます。橋は最大で二重橋までで、斜めにはかけられません。他の数字の上をスルーすることはできません。また、全体が一つに繋がっていないといけません。複数の島に分離してしまうのはNGです。

おさらい

今回も基本の条件設定を使います。

「ｎ個の量子ビットからｍ個を１にする」

その他の設定可能な条件式も気になる方は過去のまとめ記事をご参照ください。

どうやって橋をかけろを解くのか

まず、橋がかかる可能性がある場所すべてに二重線を引き、それぞれを量子ビットに対応させます。今回の問題では16量子ビット使います。量子ビットが１になれば橋がかかったことになります。

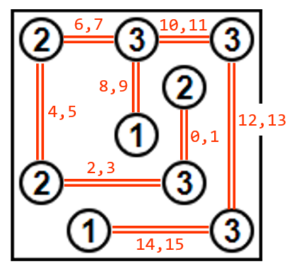
あとは、数字に着目して「可能性がある橋の中から数字の個数だけ1になる」という設定を繰り返していきます。数字が９個あるので条件式も９式ということになります。

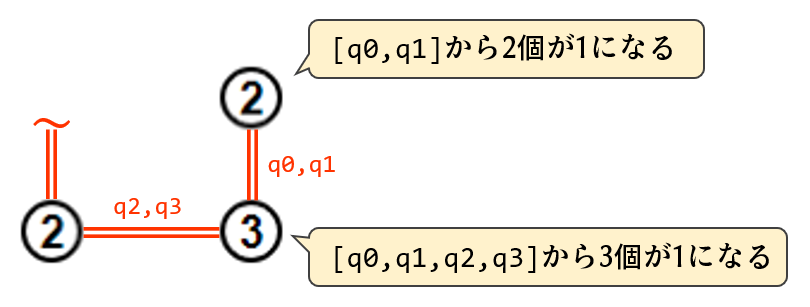
今回の問題は簡単なので、全体が一つに繋がっていないといけないという制約は特に設定しません。難しい問題になるとそれも必須になるかもしれないのでご注意ください（なお設定方法は分からない）。

コード

一気に載せてしまいます。条件設定の部分をよく確認してください。

from pyqubo import Binary
from dwave_qbsolv import QBSolv

#量子ビットを用意する
q00 = Binary('q00')
q01 = Binary('q01')
q02 = Binary('q02')
q03 = Binary('q03')
q04 = Binary('q04')
q05 = Binary('q05')
q06 = Binary('q06')
q07 = Binary('q07')
q08 = Binary('q08')
q09 = Binary('q09')
q10 = Binary('q10')
q11 = Binary('q11')
q12 = Binary('q12')
q13 = Binary('q13')
q14 = Binary('q14')
q15 = Binary('q15')

#各数字について「可能性がある橋の中から数字の個数だけ1になる」
H = 0
H += (q00 + q01 - 2)**2
H += (q00 + q01 + q02 + q03 - 3)**2
H += (q02 + q03 + q04 + q05 - 2)**2
H += (q04 + q05 + q06 + q07 - 2)**2
H += (q06 + q07 + q08 + q09 + q10 + q11 - 3)**2
H += (q08 + q09 - 1)**2
H += (q10 + q11 + q12 + q13 - 3)**2
H += (q12 + q13 + q14 + q15 - 3)**2
H += (q14 + q15 - 1)**2

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'qubo\n{qubo}')
print(f'offset\n{offset}')

#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')

response
Sample:[1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0] Energy:-50.0 Occurrence:5
Sample:[1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1] Energy:-50.0 Occurrence:6
Sample:[1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1] Energy:-50.0 Occurrence:4
Sample:[1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1] Energy:-50.0 Occurrence:4
Sample:[1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0] Energy:-50.0 Occurrence:8
Sample:[1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0] Energy:-50.0 Occurrence:1
Sample:[1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0] Energy:-50.0 Occurrence:4
Sample:[1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1] Energy:-50.0 Occurrence:6
Sample:[1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1] Energy:-50.0 Occurrence:10
Sample:[1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1] Energy:-50.0 Occurrence:4
Sample:[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0] Energy:-50.0 Occurrence:5
Sample:[1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1] Energy:-50.0 Occurrence:12
Sample:[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0] Energy:-50.0 Occurrence:6
Sample:[1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0] Energy:-50.0 Occurrence:6
Sample:[1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1] Energy:-50.0 Occurrence:6
Sample:[1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1] Energy:-50.0 Occurrence:5
Sample:[1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1] Energy:-50.0 Occurrence:5
Sample:[1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0] Energy:-50.0 Occurrence:6
Sample:[1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0] Energy:-50.0 Occurrence:6
Sample:[1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0] Energy:-50.0 Occurrence:6

解がたくさん出ましたが、実質１パターンです。1本橋は [1, 0] でも [0, 1] でも表現できるため、解がプチ組合せ爆発を起こしています。

「いや、そういうの気になるんだよなぁ」という方は次のように「弱い条件設定」を追加しましょう。偶数ビットを奇数ビットに対して少しだけ1になりやすくします。こうすると [0, 1] より [1, 0] が優先されます。

#（弱い条件）偶数ビットの方がほんの少しだけ1になりやすくする（＝[0, 1]より[1, 0]を優先する）
H += 0.1 * (q00 - 1)**2
H += 0.1 * (q02 - 1)**2
H += 0.1 * (q04 - 1)**2
H += 0.1 * (q06 - 1)**2
H += 0.1 * (q08 - 1)**2
H += 0.1 * (q10 - 1)**2
H += 0.1 * (q12 - 1)**2
H += 0.1 * (q14 - 1)**2

response
Sample:[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0] Energy:-50.8 Occurrence:493
Sample:[1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0] Energy:-50.7 Occurrence:3
Sample:[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0] Energy:-50.7 Occurrence:5
Sample:[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1] Energy:-50.7 Occurrence:1
Sample:[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0] Energy:-48.8 Occurrence:3
Sample:[1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0] Energy:-48.8 Occurrence:1

はい、これで最適解が１パターンに絞られました！橋をかけると模範解答の通りになります。