やること
QUBOでペンシルパズルの類を解くには、一つ一つのマス目に量子ビットを対応させるのがシンプルです。したがって、マス目を白か黒で塗るとか、そういった二値を決めるパズルとの相性が良いことになります。一方、数独のように整数を書き込むパズルではOne-hot表現を使うことになり、必要な量子ビット数や条件設定数がドカンと増えてしまいます。
要するに、二値タイプは設定がシンプル、整数タイプは設定が大変ということです。
今回はQUBOでカクラス(Kakurasu)を解いてみましょう。マス目を白黒に塗る二値タイプではありますが、掛け算の計算が必要な点で設定が少し難しいです。
このような問題です。
答えがこちらです。
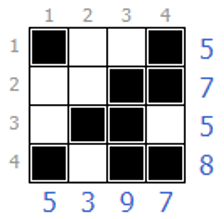
上辺・左辺の小さな数字が各列のマスの重みです。白マスを0、黒マスを1と考えて、各列の重み付き合計値が右辺・下辺の数字と一致するように塗っていきます。例えば、一番上の行は 1×1+2×0+3×0+4×1=5 を意味しています(赤字がマスの色に対応)。
おさらい
今回は基本の条件設定を使います。いや、改造して使うので原型を留めないかもしれませんが。。
基本「n個の量子ビットからm個を1にする」
その他の設定可能な条件式も気になる方は過去のまとめ記事をご参照ください。
どうやってカクラスを解くのか
16個の量子ビットを各マスに対応させます。結果が1なら黒マス(=重み有効)になります。
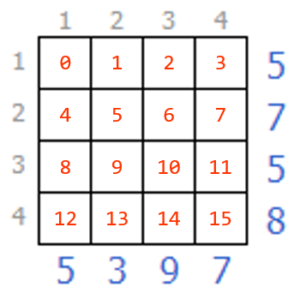
一行だけ取り出してみます。ルール説明でも述べた通り「1×q0+2×q1+3×q2+4×q3=5」にしたいです。

ここで基本の条件設定を思い浮かべてほしいのですが、「4個の量子ビットからm個を1にする」は次の式でした。
H = (q0 + q1 + q2 + q3 - m)**2これはつまり、4個の量子ビットを足した値がmになるということです。合計値がmであればエネルギーは最小で、合計値がmからずれるとエネルギーが高くなります。
ここで、4つの量子ビットに重みをかけてみます。
H = (1*q0 + 2*q1 + 3*q2 + 4*q3 - 5)**2実はこれで式は完成です。「1×q0+2×q1+3×q2+4×q3」の部分が5のときにエネルギーは最小で、5からずれるとエネルギーが高くなります。
コード
条件設定の部分をよく確認してください。
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
q00 = Binary('q00')
q01 = Binary('q01')
q02 = Binary('q02')
q03 = Binary('q03')
q04 = Binary('q04')
q05 = Binary('q05')
q06 = Binary('q06')
q07 = Binary('q07')
q08 = Binary('q08')
q09 = Binary('q09')
q10 = Binary('q10')
q11 = Binary('q11')
q12 = Binary('q12')
q13 = Binary('q13')
q14 = Binary('q14')
q15 = Binary('q15')
#各行、「重み付き合計値が指定の値になる」
H = 0
H += (1*q00 + 2*q01 + 3*q02 + 4*q03 - 5)**2
H += (1*q04 + 2*q05 + 3*q06 + 4*q07 - 7)**2
H += (1*q08 + 2*q09 + 3*q10 + 4*q11 - 5)**2
H += (1*q12 + 2*q13 + 3*q14 + 4*q15 - 8)**2
#各列、「重み付き合計値が指定の値になる」
H += (1*q00 + 2*q04 + 3*q08 + 4*q12 - 5)**2
H += (1*q01 + 2*q05 + 3*q09 + 4*q13 - 3)**2
H += (1*q02 + 2*q06 + 3*q10 + 4*q14 - 9)**2
H += (1*q03 + 2*q07 + 3*q11 + 4*q15 - 7)**2
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')Sample:[1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1] Energy:-327.0 Occurrence:390
Sample:[1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1] Energy:-324.0 Occurrence:30
Sample:[1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1] Energy:-324.0 Occurrence:45
Sample:[0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1] Energy:-323.0 Occurrence:18
Sample:[0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1] Energy:-323.0 Occurrence:1
Sample:[1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1] Energy:-323.0 Occurrence:22一番目の解を4×4に戻してやると模範解答の通りになりました。
[[1 0 0 1]
[0 0 1 1]
[0 1 1 0]
[1 0 1 1]]
さいごに
今回のように定量的なコスト(ペナルティ)を使うのは 巡回セールスマン問題 以来かもしれません。使いこなせるようになりたいですね。