やること
わざわざアニーリングで解くことではないですが、比例代表選挙におけるドント方式での議席の取り方をQUBO化してみましょう。ドント方式については社会科の教科書を発掘してください。
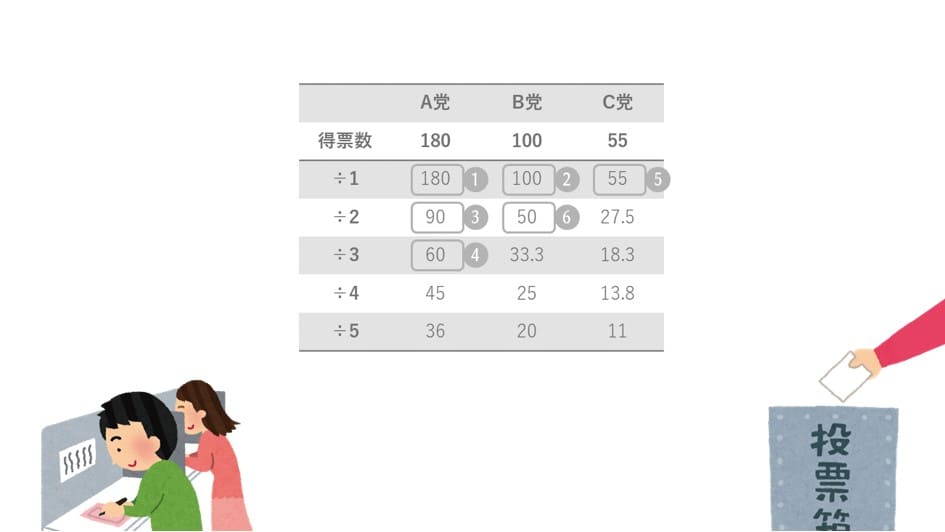
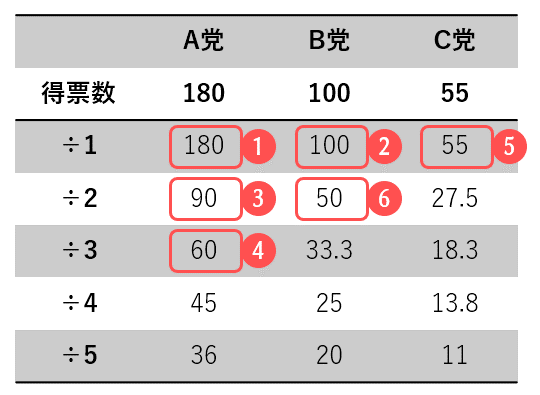
例えば、6議席を得票数180, 100, 55で争う場合は次のとおりです。
TYTANについて
「TYTAN」はOSSのアニーリングSDKです。いろいろ便利な関数が用意されています。
チュートリアル一覧
discordコミュニティ(参加リンク↓)
https://discord.gg/qT5etstPW8
おさらい
QUBOで設定できる条件式についてはこちらの記事にまとめてあります。
考え方
まず、商を÷5まで考えるとして5行3列の量子ビットを用意します。アニーリングして1になった部分が議席獲得です。
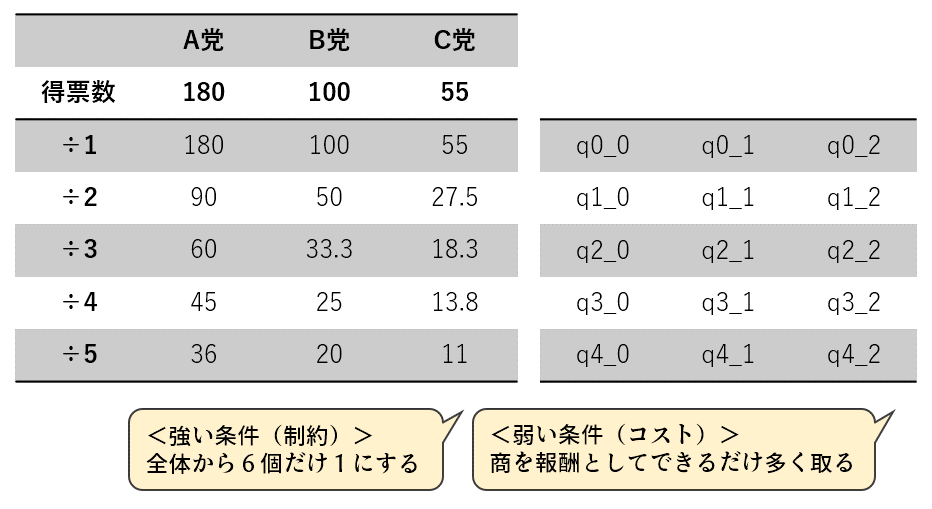
強い条件(制約)として、すべての量子ビットから6個だけ1にします。これで6議席になります。
弱い条件(コスト)として、割ってできた商を報酬として「できるだけ多くの報酬を取るように」を設定します。量子ビットが1ならその報酬が取れます。
このままでは7個でも8個でも取ったらええやん!となるので制約は重み10、コストは重み0.01と差をつけます。こうすれば、1議席多く取るペナルティが10、商180を取る報酬が1.8になるため制約が優先的されます。
コード1
from tytan import *
import numpy as np
#得票数
a = np.array([180, 100, 55])
b = np.array([a/1, a/2, a/3, a/4, a/5], float)
print(b)
#量子ビットの用意
q = symbols_list([5, 3], 'q{}_{}')
print(q)
#議席数だけ1にする(強い条件)
H = 0
tmp = 0
for i in range(5):
for j in range(3):
tmp += q[i, j]
H += 10 * (tmp - 6)**2
#得票数を割ってできた数字を報酬とする(弱い条件)
for i in range(5):
tmp = 0
for j in range(3):
tmp -= b[i, j] * q[i, j]
H += 0.01 * tmp
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.SASampler()
#サンプリング
result = solver.run(qubo)
for r in result:
print(r)
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
print(arr)[[180. 100. 55. ]
[ 90. 50. 27.5 ]
[ 60. 33.33333333 18.33333333]
[ 45. 25. 13.75 ]
[ 36. 20. 11. ]]
[[q0_0 q0_1 q0_2]
[q1_0 q1_1 q1_2]
[q2_0 q2_1 q2_2]
[q3_0 q3_1 q3_2]
[q4_0 q4_1 q4_2]]
offset
360
[{'q0_0': 1, 'q0_1': 1, 'q0_2': 1, 'q1_0': 1, 'q1_1': 1, 'q1_2': 0, 'q2_0': 1, 'q2_1': 0, 'q2_2': 0, 'q3_0': 0, 'q3_1': 0, 'q3_2': 0, 'q4_0': 0, 'q4_1': 0, 'q4_2': 0}, -365.35, 100]
[[1 1 1]
[1 1 0]
[1 0 0]
[0 0 0]
[0 0 0]]結果は1通りで、順に3・2・1議席を獲得したことが分かります。
コード2
今度は、B党の得票数を135に変えて、さらに全体の議席数を7に増やしてみるとどうなるでしょうか?
[[180. 135. 55. ]
[ 90. 67.5 27.5 ]
[ 60. 45. 18.33333333]
[ 45. 33.75 13.75 ]
[ 36. 27. 11. ]]
offset
490
[{'q0_0': 1, 'q0_1': 1, 'q0_2': 1, 'q1_0': 1, 'q1_1': 1, 'q1_2': 0, 'q2_0': 1, 'q2_1': 0, 'q2_2': 0, 'q3_0': 1, 'q3_1': 0, 'q3_2': 0, 'q4_0': 0, 'q4_1': 0, 'q4_2': 0}, -496.325, 28]
[[1 1 1]
[1 1 0]
[1 0 0]
[1 0 0]
[0 0 0]]
[{'q0_0': 1, 'q0_1': 1, 'q0_2': 1, 'q1_0': 1, 'q1_1': 1, 'q1_2': 0, 'q2_0': 1, 'q2_1': 1, 'q2_2': 0, 'q3_0': 0, 'q3_1': 0, 'q3_2': 0, 'q4_0': 0, 'q4_1': 0, 'q4_2': 0}, -496.325, 72]
[[1 1 1]
[1 1 0]
[1 1 0]
[0 0 0]
[0 0 0]]結果は4・2・1議席と3・3・1議席の2通りになりました。最後の1議席を取る商(45)が2箇所あるため、どちらを取るかで分かれたようです。
「商が同数の場合はくじ引きで」という情報もあるようですが、ここでは「迷ったときは得票数が多い党を優先する」というルールにしてみましょう。
#得票数の多い党を少し優先(弱い条件)
for i in range(5):
H += 0.02 * (q[i, 0] - 1)**2
H += 0.01 * (q[i, 1] - 1)**2offset
490.15
[{'q0_0': 1, 'q0_1': 1, 'q0_2': 1, 'q1_0': 1, 'q1_1': 1, 'q1_2': 0, 'q2_0': 1, 'q2_1': 0, 'q2_2': 0, 'q3_0': 1, 'q3_1': 0, 'q3_2': 0, 'q4_0': 0, 'q4_1': 0, 'q4_2': 0}, -496.425, 100]
[[1 1 1]
[1 1 0]
[1 0 0]
[1 0 0]
[0 0 0]]これで結果が絞られました。
さいごに
2023/7/19現在、QUBOマスター認定者は7名です。めざせQUBOマスター。