やること
「大学入試史上最も難しい数学の問題」と言われているのが1998年の東京大学、後期第3問。大手予備校が当日に解答速報を出せなかったとか。

今回はこのグラフ理論の問題をPythonで解いてみたいと思います。先に言っておきますが(2)は全探索すると無限の時間がかかるので解けていません。
どんな問題?
引用ですみません。問題、解答、予備校が解答速報を出せなかった逸話がすべてこちらのサイトにまとまっているのでご参照ください。感謝します。

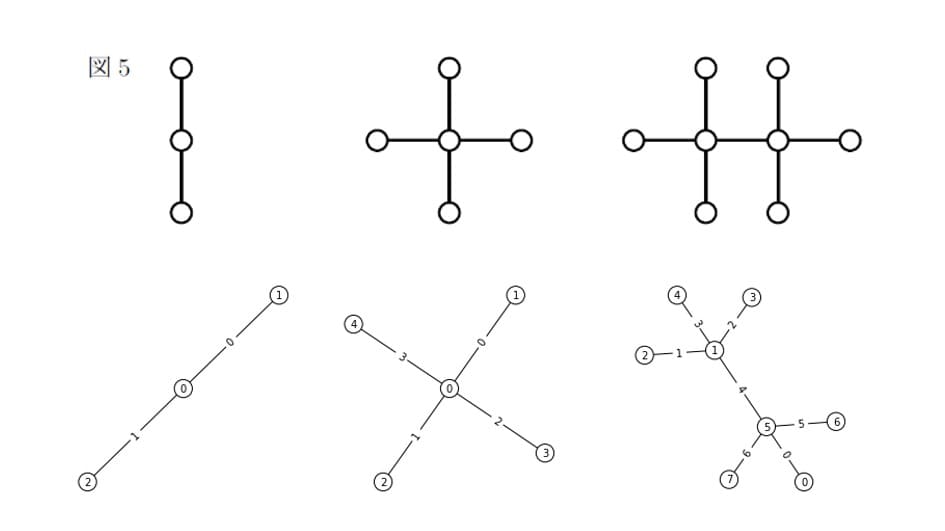
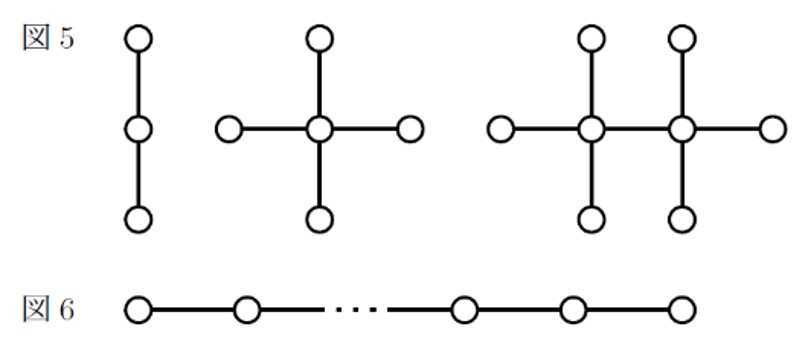
問(1)は、初期状態から操作1と操作2を繰り返すことで図5の各グラフが作成可能であることを示すというもの。問(2)では図6が可能グラフになるための必要十分条件を求めます(正解者ゼロ)。
可視化の関数、操作1, 2の関数
さっそくプログラミングしていきましょう。
グラフの操作にはお馴染みの「networkx」を使います。
import os
import numpy as np
from copy import deepcopy
import matplotlib.pyplot as plt
import networkx as nxまずは可視化の関数です。
def show(G):
#ノード色
whites = [G.nodes[node]['white'] for node in G.nodes()]
node_colors = ['w' if white == 1 else 'k' for white in whites]
font_colors = ['k' if white == 1 else 'w' for white in whites]
#
plt.figure()
pos = nx.spring_layout(G) #kの値が小さい程図が密集する
#ノードとエッジの描画
nx.draw_networkx_nodes(G, pos, node_color=node_colors, edgecolors='k')
nx.draw_networkx_edges(G, pos, edge_color='k')
#ノード名を付加
for i in range(nx.number_of_nodes(G)):
nx.draw_networkx_labels(G, pos, labels={i: f'{i}'}, font_color=font_colors[i], font_size=10)
#エッジ名を付加
edge_labels = nx.get_edge_attributes(G, 'label')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
#X軸Y軸を表示しない
plt.axis('off')
plt.show()初期ノードを表示してみます。
#初期化
G = nx.Graph()
G.add_node(0, white=1)
show(G)
操作1の関数を作って実行します。指定したノードに新規ノードをくっつけて色を整えます。
def action1(G, target_node):
#コピー
G2 = deepcopy(G)
#新規ノード番号とエッジ
new_node = nx.number_of_nodes(G2)
new_edge = nx.number_of_edges(G2)
#新規ノードを付ける
G2.add_edge(target_node, new_node, label=new_edge)
#新規ノードを白にする
G2.nodes[new_node]['white'] = 1
#ターゲットノードを反転する
G2.nodes[target_node]['white'] *= -1
return G2
#操作1
G = action1(G, 0)
show(G)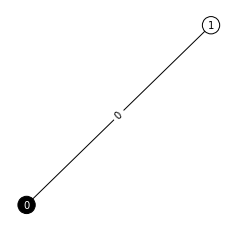
ノード0に対して新しいノードがくっつきました。
同様に操作2の関数を作って実行します。指定したエッジを切り、そこに新規ノードを挟み込んで色を整えます。
def action1(G, target_node):
#コピー
G2 = deepcopy(G)
#新規ノード番号とエッジ
new_node = nx.number_of_nodes(G2)
new_edge = nx.number_of_edges(G2)
#新規ノードを付ける
G2.add_edge(target_node, new_node, label=new_edge)
#新規ノードを白にする
G2.nodes[new_node]['white'] = 1
#ターゲットノードを反転する
G2.nodes[target_node]['white'] *= -1
return G2
#操作2
G = action2(G, 0)
show(G)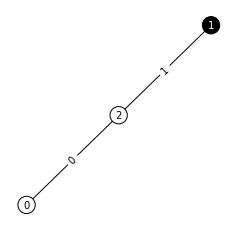
エッジ0に新しいノードが挿入されました。
探索の関数
パーツを一個作ります。ある枝分かれ数を持つノードの数を調べて返す関数です。
#ある枝分かれ数を持つノードの数
def num_nodes_with_degree(G, degree):
nodes_with_degree = [node for node, deg in G.degree() if deg == degree]
return len(nodes_with_degree)この関数は、例えば次のグラフをdegree=4で調べると2が返ってきます。(4本腕を持つノードが2つあるという意味)

ここからはガチで。ノードを増やしながら全探索する再帰関数を作ります。
#再帰関数
def do_all_action(G):
global count
#規定のノード数であれば再帰を終了
if nx.number_of_nodes(G) == 3:
#ノードが全部白、かつ、ある枝分かれ数を持つノードの数が規定通りなら表示
whites = [G.nodes[node]['white'] for node in G.nodes()]
num = num_nodes_with_degree(G, 2)
if set(whites) == {1} and num == 1:
print('found!!')
show(G)
raise
return
#すべてのノードとエッジ
node_list = np.arange(nx.number_of_nodes(G))
edge_list = np.arange(nx.number_of_edges(G))
#各ノードに操作1をしてから再帰送り
for target_node in node_list:
G2 = action1(G, target_node)
count += 1
if count % 10000 == 0: print(count)
do_all_action(G2)
#各エッジに操作2をしてから再帰送り
for target_edge in edge_list:
G2 = action2(G, target_edge)
count += 1
if count % 10000 == 0: print(count)
do_all_action(G2)再帰関数をうまく作るコツを紹介します。まず冒頭に終了条件。ここでは分かりやすく「raise」でプログラム自体を強制終了させます。その後に自身を呼び出す部分を書くのですが、主人公であるグラフ(G)は、現在の世界線(スコープ)で使っているものをそのまま次の世界線に渡してしまうと上書きでぶっ壊れたりするので、deepcopyした別人(G2)を渡すようにします。今回は操作1と2の中でdeepcopyして別人を作成しています。まあ、伝われ。
問(1)
1個目
では、グラフを初期化して再帰探索してみましょう。問(1)の1個目は◯-◯-◯を作れというものなので終了条件は次のとおり。ノード数3で、degree=2が1個になったら終了です。
#規定のノード数であれば再帰を終了
if nx.number_of_nodes(G) == 3:
#ノードが全部白、かつ、ある枝分かれ数を持つノードの数が規定通りなら表示
whites = [G.nodes[node]['white'] for node in G.nodes()]
num = num_nodes_with_degree(G, 2)
if set(whites) == {1} and num == 1:
print('found!!')
show(G)
raise
return探索開始。
#初期化
G = nx.Graph()
G.add_node(0, white=1)
show(G)
#総探索数
count = 0
#探索
do_all_action(G)found!!
Traceback (most recent call last):
(中略)
File main.py:116 in do_all_action
raise
RuntimeError: No active exception to reraise
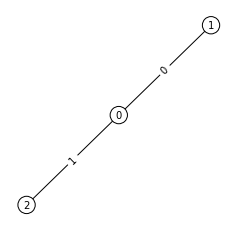
すぐに発見しました。手順は簡単にバックトレースできると思います。
2個目
2個目はメタンを作れということで、ノード数5、degree=4が1個になったら終了です。
found!!
Traceback (most recent call last):
(中略)
File main.py:116 in do_all_action
raise
RuntimeError: No active exception to reraise
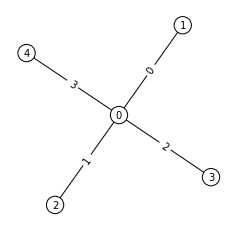
こちらも一瞬でした。
3個目
最後はエタンを作れということで、ノード数5、degree=4が2個になったら終了です。
10000
20000
30000
40000
50000
60000
found!!
Traceback (most recent call last):
(中略)
File main.py:116 in do_all_action
raise
RuntimeError: No active exception to reraise
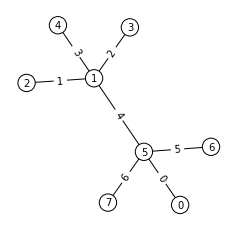
出ました。1万世界線ごとにprintしているので、6~7万世界で見つかったことが分かります。ちゃんと可能グラフであることが示せました。
問(2)
問(2)は証明問題なのでちょっとPythonでは太刀打ちできないのですが、n=4から全探索してみます。
n=4
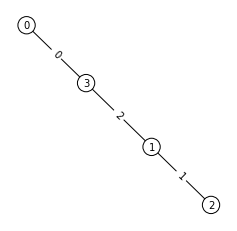
n=5
発見できず
n=6
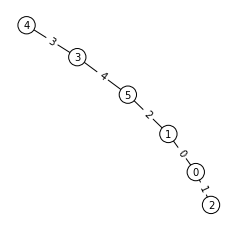
n=7

n=8
発見できず
n=9

n=10
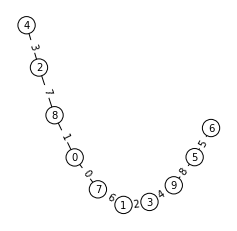
n=11
発見できず
n=12の探索は1時間以上かかりそうなので諦めました。スパコン持っている方はお願いします。
可能グラフになるための必要十分条件は「n=3k-2, 3k (kは自然数)」とのことなので、n=11までは矛盾しない結果が得られたことになります。この辺が限界ですね。
さいごに
数学の証明には無限を見通す力があることを改めて感じました。今回はグラフの操作の練習にちょうどよかったと思います。