やること
こんにちは、Suzuです _( _・ヮ・)_
今回は魔法陣グルグルという漫画に出てくる魔法陣が一筆書きできるかを検証します。
魔法陣グルグルは主人公の二ケとククリが魔王打倒のために冒険するというストーリーです。月間少年ガンガンに1992年から2003年にかけて連載されました。実家に漫画が揃っています。2017年にアニメ放送もやっていました。これもDMMで観ました。とても面白い(小並)
一筆書きとは全ての辺を1回ずつ通るように連続的な線を書くことです。一筆書きはグラフ理論で分析できます。グラフはいくつかの点とそれらを結ぶ線で構成される図形です。
さっそく見ていきましょう。
参考文献
魔法陣グルグルの魔法陣一覧です
オイラーグラフについて

オイラーグラフとハミルトングラフについて
ハミルトン閉路について
https://school.gifu-net.ed.jp/ena-hs/ssh/H29ssh/sc3/31701.pdf
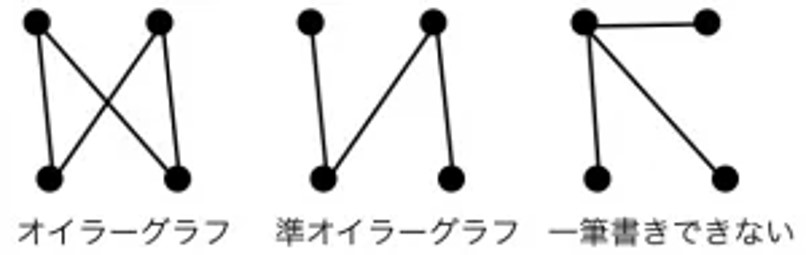
オイラーグラフと準オイラーグラフ
オイラーグラフは一筆書きして出発点(始点)に戻って来ることができるグラフです。つまり、全ての辺を1回だけ通過して元に戻れるグラフです。
一方、準オイラーグラフは一筆書きすることはできるが出発点(始点)に戻って来ることができないグラフです。始点と終点が異なります。
各頂点において、その頂点から出ている辺の本数をその頂点の次数と呼びます。つまり、頂点Aから出ている辺が3つあれば頂点Aの次数は3となります。このとき、次数が偶数であれば偶点、奇数であれば奇点と呼びます。
ハミルトングラフとは
別の名前のグラフもあります。ハミルトングラフは全ての点を一度だけ通過して元に戻れるグラフを指します。先程のオイラーグラフは実はハミルトングラフでもあります。
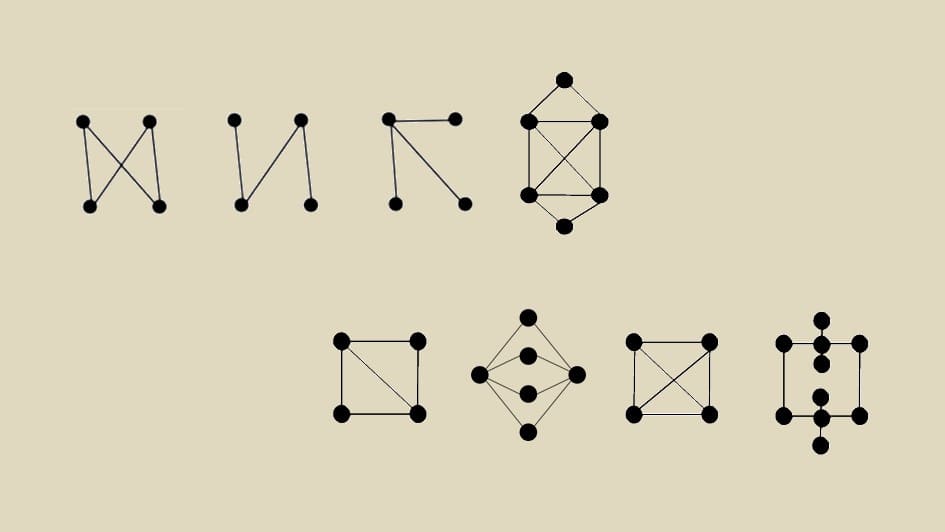
いろいろなグラフを見てみる
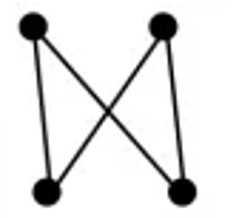
例1
こちらのグラフはオイラーグラフとハミルトングラフに該当します。図では全ての辺を通ってオイラーグラフであることを確認しています。ハミルトングラフの確認では全ての点を通りますが、同じ点を2度通れないので別の奇跡になることに注意してください(辺が余ります)。
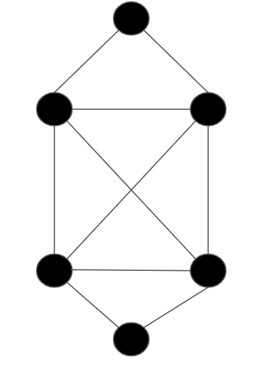
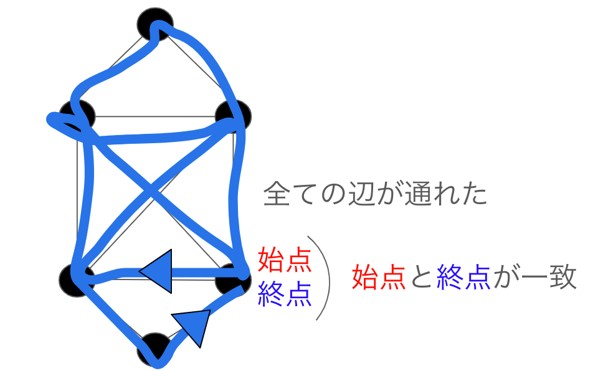
例2
こちらは準オイラーグラフとハミルトングラフに該当します。一筆書きで全ての辺を通ることができますが、始点と終点が一致しません。ハミルトングラフの確認ではやはり辺が余ります。
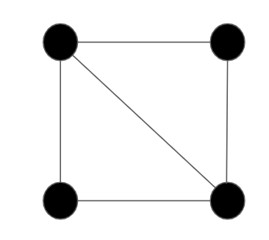
例3
こちらはオイラーグラフのみに該当します。一筆書きで全ての辺を通って元に戻れます。一方、全ての点を1度だけ通って始点に戻ることができないためハミルトングラフではありません。
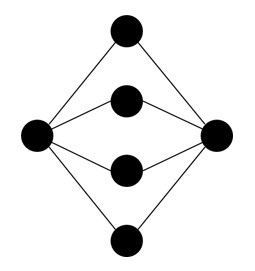
例4
こちらはハミルトングラフのみに該当します。一筆書きで全ての辺を通ることができません。
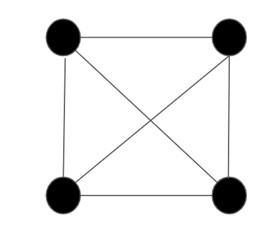
例5
こちらはオイラーグラフでもハミルトングラフでもありません。枝が3本以上生えているので明らかです。
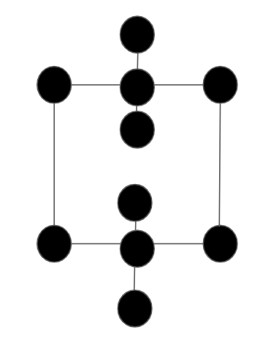
まとめ
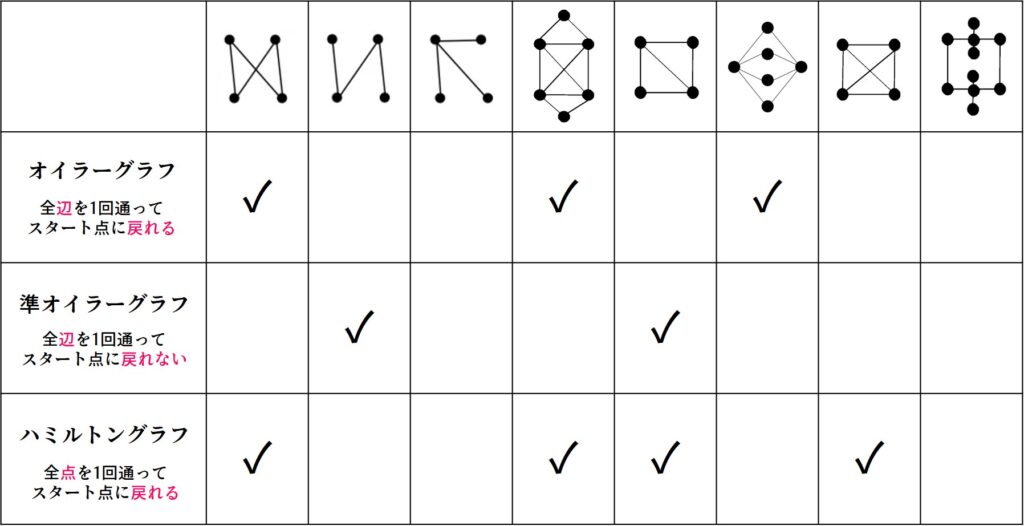
ここまでに登場したグラフをまとめました。もし間違いがあったら教えてください。
さいごに
次回はいよいよ魔法陣グルグルの魔法陣を見ていきます↓