21-3. D-waveマシンで大規模な問題を解く準備（設定の関数化、問題の分割解法）

量子コンピュータ

2019/11/07

やること
実行環境
参考記事
量子ビットをｋ個用意する
ｎ個の量子ビットからｍ個を１にする
一旦試してみる
テクニック１（任意）
テクニック２（必須）―問題の分割解法―
まとめ

やること

前回はD-waveの設定を一つ一つ手書きして、小さなパズル問題を解きました。設定は36行にも及びました。

しかし、設定を一つ一つ手書きするのでは、より大きな問題に挑戦する気が起きません。今回は、この設定を関数化して便利にしてみます。また、大きな問題を解くために必須のテクニックも学びます。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

参考記事

初学者の方は21-1から順番にフォローしていただければと思います。

量子ビットをｋ個用意する

量子ビットを４つ用意するコマンドは次のとおりでした。

#量子ビットを４つ用意する
q0, q1, q2, q3  = Binary('q0'), Binary('q1'), Binary('q2'), Binary('q3')

これを、num=4 だけ与えれば適当にやってくれるようにします。愚直ですが、「q0 = Binary(‘q0’)」といった文字列を用意してexec()で実行していきます。

#量子ビットを４つ用意する
for i in range(4):
    command = 'q{} = Binary(\'q{}\')'.format(i, i)
    print(command)
    exec(command)

q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
q3 = Binary('q3')

できました！数字を書き変えるだけでたくさんの量子ビットを用意できます。

ｎ個の量子ビットからｍ個を１にする

「４個の量子ビットから２個を１にする」は次のとおりでした。

#条件を記述する
H = (q0 + q1 + q2 + q3 - 2)**2

この部分も、list=[0, 1, 2, 3] と num=2 を与えるだけで適当にやってくれるように関数化します。

まず、試しに次を実行してみました。

a = '+'.join(['q{}'.format(i) for i in [0, 1, 2, 3]])
print(a)

q0+q1+q2+q3

ちょうど ‘H = (q0 + q1 + q2 + q3 – 2)**2’ の一部になりました。

これをもとに、次の関数を作りました。文字式として書かれた数式を評価する eval() を用います。

#条件を記述する関数
def H_add(qbits, num):
    command = '(' + '+'.join(['q{}'.format(i) for i in qbits]) + '-{})**2'.format(num)
    print(command)
    return eval(command)

#条件を記述する
H = H_add([0, 1, 2, 3], 2)

(q0+q1+q2+q3-2)**2

できました！

一旦試してみる

「４個の量子ビットから２個を１にする」は次のように進化しました。（元のコードよりも長くなりましたが、後々楽になるはず）

from pyqubo import Binary
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler

#量子ビットを４つ用意する
for i in range(4):
    command = 'q{} = Binary(\'q{}\')'.format(i, i)
    print(command)
    exec(command)

#条件を記述する関数
def H_add(qbits, num):
    command = '(' + '+'.join(['q{}'.format(i) for i in qbits]) + '-{})**2'.format(num)
    print(command)
    return eval(command)

#条件を記述する
H = H_add([0, 1, 2, 3], 2)

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#print('qubo\n{}'.format(qubo))

#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
                                          token='your_token',
                                          solver='DW_2000Q_5'))

#サンプリングしまくる
response = sampler.sample_qubo(qubo, num_reads=1000)

#レスポンスの確認
print('response')
for (sample, energy, occurrence, _) in response.data():
    print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))

q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
q3 = Binary('q3')
(q0+q1+q2+q3-2)**2
response
Sample:[1, 1, 0, 0] Energy:-4.0 Occurrence:132
Sample:[1, 0, 1, 0] Energy:-4.0 Occurrence:182
Sample:[0, 1, 1, 0] Energy:-4.0 Occurrence:149
Sample:[1, 0, 0, 1] Energy:-4.0 Occurrence:152
Sample:[0, 1, 0, 1] Energy:-4.0 Occurrence:152
Sample:[0, 0, 1, 1] Energy:-4.0 Occurrence:144
Sample:[0, 0, 1, 1] Energy:-4.0 Occurrence:1
Sample:[1, 0, 0, 1] Energy:-4.0 Occurrence:2
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:3
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:2
Sample:[0, 1, 1, 1] Energy:-3.0 Occurrence:11
Sample:[1, 0, 1, 1] Energy:-3.0 Occurrence:6
Sample:[1, 1, 1, 0] Energy:-3.0 Occurrence:8
Sample:[0, 0, 0, 1] Energy:-3.0 Occurrence:15
Sample:[0, 1, 1, 1] Energy:-3.0 Occurrence:1
Sample:[0, 0, 1, 0] Energy:-3.0 Occurrence:13
Sample:[0, 1, 0, 0] Energy:-3.0 Occurrence:6
Sample:[1, 0, 0, 0] Energy:-3.0 Occurrence:8
Sample:[1, 1, 0, 1] Energy:-3.0 Occurrence:11
Sample:[0, 1, 1, 1] Energy:-3.0 Occurrence:2

動作は良さそうですね！

テクニック１（任意）

実務上の細かい話になりますが、量子ビットを11個以上用意するとき、q0～q10という感じで定義すると、サンプリングの結果が [q0, q1, q10, q2, q3, … , q9] といった順番で格納され、扱いづらくなります。（結果をそのまま代入なんてしたらめちゃくちゃな順番で入ります）

これを解消するには、21-2の記事でも行っているように、q00～q10という感じで２桁のゼロ埋めで定義します。これで結果が [q00, q01, q02, q03, … , q10] と自然順になります。２桁のゼロ埋めであれば100量子ビットまで安心ですし、３桁にすれば1000量子ビットまで安心です。

#量子ビットを４つ用意する
for i in range(4):
    command = 'q{:03} = Binary(\'q{:03}\')'.format(i, i)
    print(command)
    exec(command)

#条件を記述する関数
def H_add(qbits, num):
    command = '(' + '+'.join(['q{:03}'.format(i) for i in qbits]) + '-{})**2'.format(num)
    print(command)
    return eval(command)

#条件を記述する
H = H_add([0, 1, 2, 3], 2)

q000 = Binary('q000')
q001 = Binary('q001')
q002 = Binary('q002')
q003 = Binary('q003')
(q000+q001+q002+q003-2)**2

テクニック２（必須）―問題の分割解法―

D-waveマシンには量子ビットが約2000個用意されていますので、「2000量子ビットまでの問題が解けるんだ！」と思ってしまいがちですが、実際には50～100量子ビット程度の問題を解こうとするとエラーが返ってきます。なぜなのでしょうか。

D-waveマシン上の量子ビットは次のように繋がって相互作用を行うことができます。一つの量子ビットは隣り合う５～６個と繋がっていますが、その他とは直接は繋がっていません。ですから、遠いところにあるビットとの相互作用を設定しようとすると、間に複数の「中継ビット」を置かなければなりません。問題の規模が大きくなり相互作用の設定が複雑になるほど、必要な中継ビットの数は急激に増えます。ですから、2000量子ビットで解ける問題の規模は思ったよりも小さいようです。

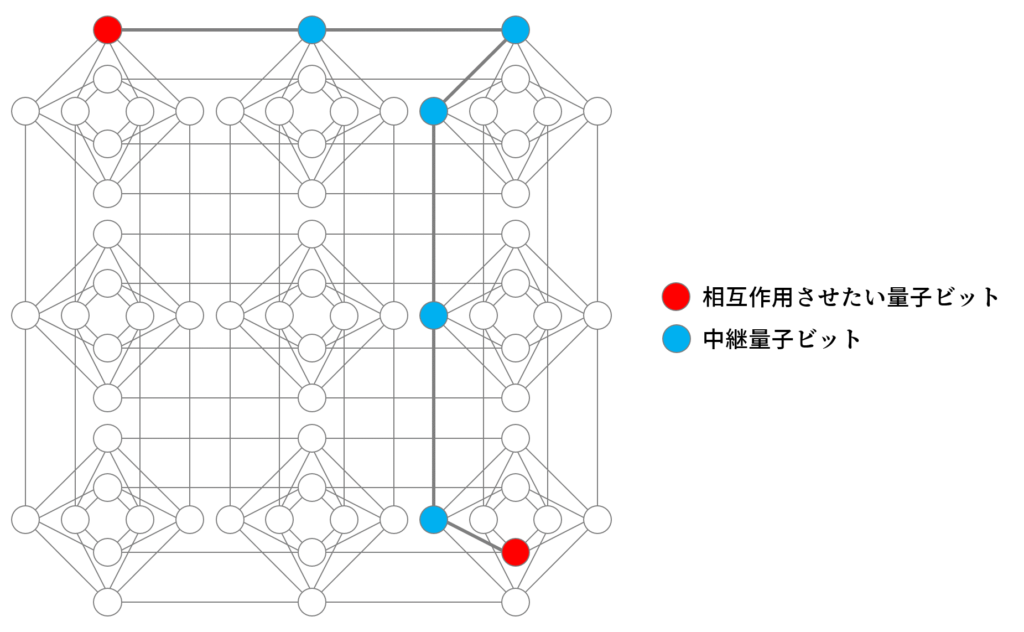
そこで、量子ビットの相互作用を表現した配列（＝QUBO）をD-waveに乗るサイズに分割して、古典最適化を併用して最適化を行う方法があります。QBSolv というパッケージを用います。

from dwave_qbsolv import QBSolv

#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
                                          token='your_token',
                                          solver='DW_2000Q_5'))

#問題を分割してサンプリングしまくる
response = QBSolv().sample_qubo(qubo, solver=sampler, num_repeats=50)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))

この方法は大域最適化ではなく、「局所最適化だけどうまいことやって大域最適化に近い答えを出す」という感じで頑張ってくれます。一定の問題規模までは、分割しない方法とほとんど同等の性能が期待できるようです。

まとめ

最終的にソースコードは次のようになりました。

from pyqubo import Binary
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler
from dwave_qbsolv import QBSolv

#量子ビットを４つ用意する
for i in range(4):
    command = 'q{:03} = Binary(\'q{:03}\')'.format(i, i)
    print(command)
    exec(command)

#条件を記述する関数
def H_add(qbits, num):
    command = '(' + '+'.join(['q{:03}'.format(i) for i in qbits]) + '-{})**2'.format(num)
    print(command)
    return eval(command)

#条件を記述する
H = H_add([0, 1, 2, 3], 2)

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#print('qubo\n{}'.format(qubo))

#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi',
                                          token='your_token',
                                          solver='DW_2000Q_5'))

#問題を分割してサンプリングしまくる
response = QBSolv().sample_qubo(qubo, solver=sampler, num_repeats=50)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print('Sample:{} Energy:{} Occurrence:{}'.format(list(sample.values()), energy, occurrence))

q000 = Binary('q000')
q001 = Binary('q001')
q002 = Binary('q002')
q003 = Binary('q003')
(q000+q001+q002+q003-2)**2
response
Sample:[0, 1, 1, 0] Energy:-4.0 Occurrence:14
Sample:[1, 0, 0, 1] Energy:-4.0 Occurrence:8
Sample:[1, 1, 0, 0] Energy:-4.0 Occurrence:5
Sample:[0, 1, 0, 1] Energy:-4.0 Occurrence:6
Sample:[0, 0, 1, 1] Energy:-4.0 Occurrence:3
Sample:[1, 0, 1, 0] Energy:-4.0 Occurrence:15

これでより大きな組合わせ最適化問題に挑む準備ができました！