やること
ボイドモデル(Boids)は、鳥の群れをシミュレーションするための人工生命モデルです。魚や陸上生物でもいいでしょう。
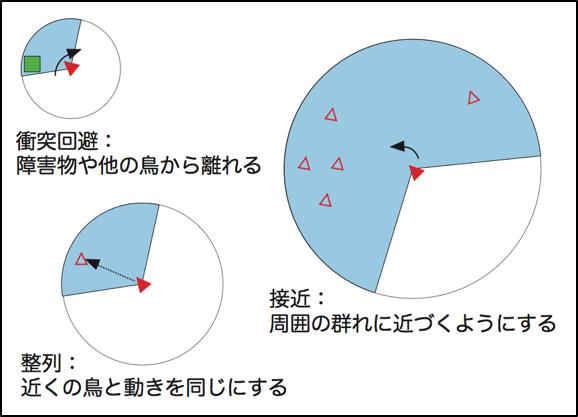
今回は、ボイドモデルを構成する3つのルールのうち「分離(衝突回避)」「結合(接近)」だけを簡易的に実装してシミュレーションしてみます。ルールには他に「整列」があります。
参考
モデルについてはこちらがわかりやすいです。
こちらのシミュレーターも楽しいです。

実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

考え方
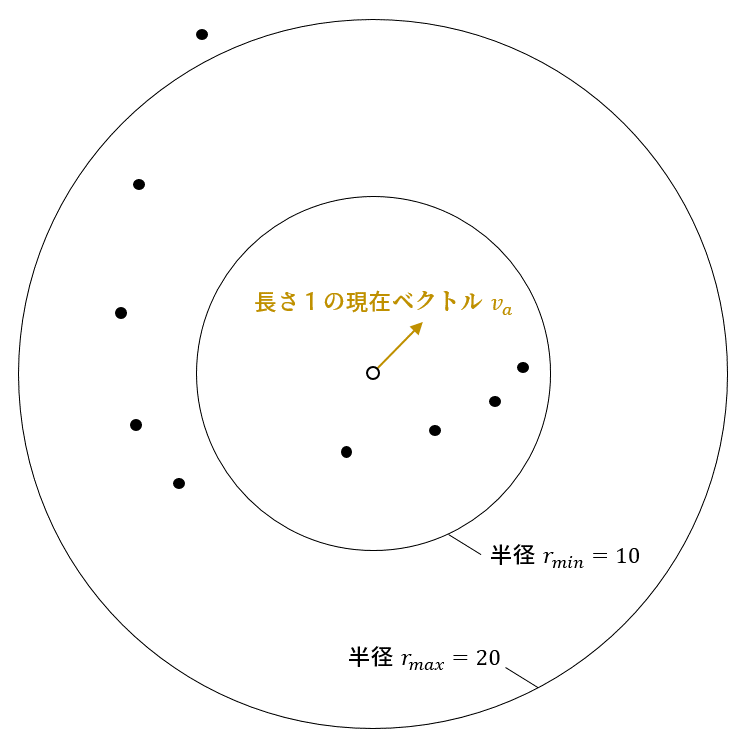
フィールドに100羽の鳥を放します。各鳥は現在ベクトル(長さ1)で進んでいます。
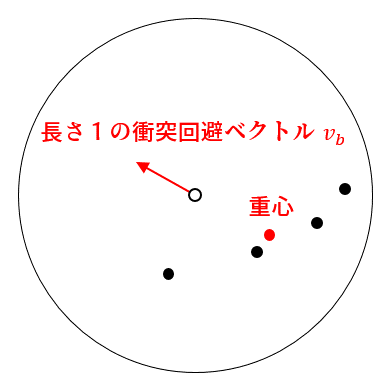
分離(衝突回避)
他の鳥と衝突したくないので、近距離の鳥たちから離れる方向に進む力を与えます。自分から見て「半径0mより遠く」かつ「半径10m以内」にいる鳥たちの重心を求め、重心とは反対方向の衝突回避ベクトル(ただし長さ1)を計算します。
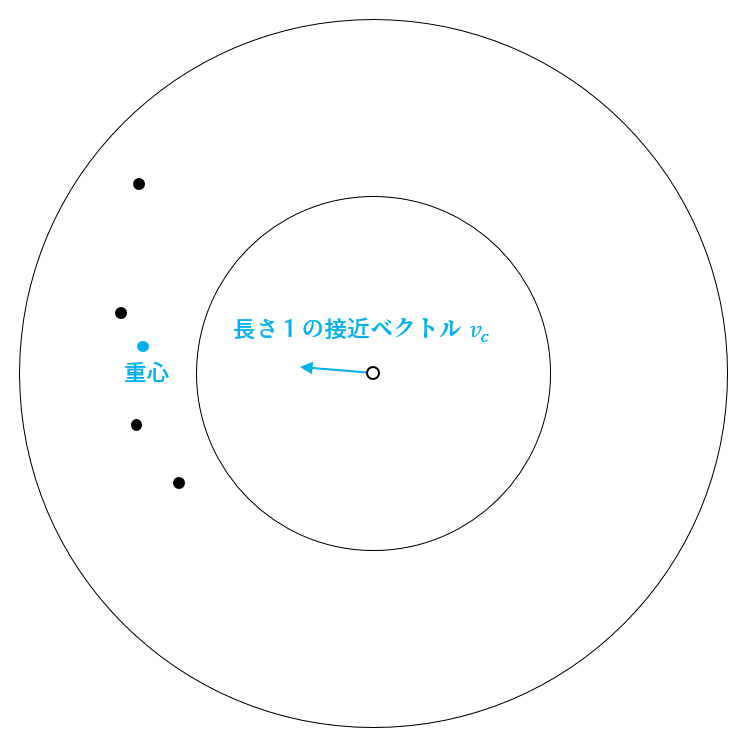
結合(接近)
群れから離れて孤立したくないので、中距離の鳥たちに近づく方向に進む力を与えます。自分から見て「半径10mより遠く」かつ「半径20m以内」にいる鳥たちの重心を求め、重心方向の接近ベクトル(ただし長さ1)を計算します。
進行ベクトルの更新
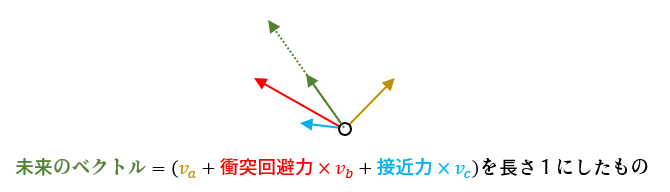
未来のベクトルは、
- 現在ベクトル
- 衝突回避ベクトル
- 接近ベクトル
を重み付けして合計したベクトル(ただし長さ1)とします。重みは「衝突回避力」「接近力」というパラメータとします。
また、シミュレーションの時間刻みを1とすると、常に速さ1で飛ぶことになります。加速や減速はしません。
import, パラメータ
「衝突回避力」と「接近力」はとりあえず (20, 0) で置いてみます。
import numpy as np
import numpy.random as nr
from copy import deepcopy
import matplotlib.pyplot as plt
#======================================
# パラメータ
#======================================
#フィールドの幅、高さ
w, h = 100, 80
#鳥の数
num = 100
#衝突回避力、接近力
#細密充填
pow_1 = 20
pow_2 = 0
#最大ステップ数
max_step = 1000関数
群れをプロットする関数、鳥同士の距離行列を計算する関数、指定した範囲内の他の鳥の重心を返す関数を作ります。
#======================================
# 関数
#======================================
#表示関数
def show(title):
plt.figure(figsize=(10, 8))
plt.scatter(pos[:, 0], pos[:, 1], c='k', s=10)
plt.xlim([0, w]), plt.ylim([0, h])
plt.title(title)
plt.show(), plt.close(), print()
#鳥同士の距離行列distを計算する関数
def recort_dist():
global dist
dist = np.zeros((num, num))
#距離を上三角行列として記録
for i in range(0, num-1):
for j in range(i+1, num):
dist[i, j] = ((pos[i, 0] - pos[j, 0])**2 + (pos[i, 1] - pos[j, 1])**2)**0.5
#下三角にもコピーして距離行列の完成
dist += dist.T
#ある鳥を基準に、半径r_minより遠くr_max以内にいる他の鳥たちの位置の重心を返す関数
def get_center_gravity(my_id, r_min, r_max):
#条件を満たす他の鳥のID
inrange_ids = np.where((dist[my_id]>r_min)*(dist[my_id]<=r_max))[0]
#いなければ自分の座標を返すが、ランダムに少しずらす
if len(inrange_ids) == 0:
return pos[my_id] + (nr.rand(2)*0.002 - 0.001)
else:
#いればそれらの重心を返す
return np.mean(pos[inrange_ids], axis=0)メイン
時間ステップを進めながら、繰り返し計算と表示を行います。こういったシミュレーションを行うときの注意点として、逐次的に計算した鳥の未来座標は一旦別の配列に記録しておき、100羽の計算が終わった後にまとめて更新(座標を上書き)します。逐次的に更新してしまうと変なことが起きますので。
なお、フィールドはトーラス状にループしています。
#======================================
# メイン
#======================================
#鳥の座標をランダム生成
pos = nr.rand(num, 2)
pos[:, 0] *= w
pos[:, 1] *= h
#鳥の速度をランダム生成
vec = nr.rand(num, 2) * 2 - 1
#繰り返しステップ
for n in range(1, max_step + 1):
#距離行列の作成
recort_dist()
#未来座標の準備
pos_next = deepcopy(pos)
#すべての鳥
for i in range(num):
#近い範囲にいる他の鳥たちの重心(0mより遠く10m以内)
cg1 = get_center_gravity(i, 0, 10)
#ベクトル(向き)
vec_cg1 = cg1 - pos[i]
#ベクトルを規格化(長さ1)
vec_cg1 /= np.linalg.norm(vec_cg1)
#遠い範囲にいる他の鳥たちの重心(10mより遠く20m以内)
cg2 = get_center_gravity(i, 10, 20)
#ベクトル(向き)
vec_cg2 = cg2 - pos[i]
#ベクトルを規格化(長さ1)
vec_cg2 /= np.linalg.norm(vec_cg2)
#進むべきベクトルを重み付けで計算(現ベクトル+衝突回避+接近)
vec_total = vec[i] - pow_1*vec_cg1 + pow_2*vec_cg2
#ベクトルを規格化(長さ1)
vec_total /= np.linalg.norm(vec_total)
#未来座標に記録(ここではposは更新しない)
pos_next[i] += vec_total
#ベクトルの更新
vec[i] = vec_total
#座標の更新
pos = deepcopy(pos_next)
#境界はトーラスにループさせる
pos[:, 0][pos[:, 0] < 0] += w
pos[:, 0][pos[:, 0] > w] -= w
pos[:, 1][pos[:, 1] < 0] += h
pos[:, 1][pos[:, 1] > h] -= h
show(n)結果1
衝突回避力=20、接近力=0
絶対衝突回避マン。群れることはない。
六方最密充填になりました。
衝突回避力=0、接近力=2
衝突は気にしない。どうしても群れたい。
ハエかな?クラスターの合流も観察されました。
衝突回避力=0、接近力=0.2
同じく衝突は気にしない。どちらかと言うと群れていたい。
なんか回りました。
衝突回避力=5、接近力=4
絶対に衝突はしたくない。でも群れていたい。つまり Social Distance.
※正しくは Social Distancing.
六方最密充填のクラスターが形成されました。
ということは検出する半径を小さくしたら複数のクラスターが見えるのかなぁ。ということで r_min=5, r_max=10 にしてみました。
なりました。合流もします。
まとめ
「分離(衝突回避)」「結合(接近)」の2つのルールだけでもそれなりのシミュレーションができることがわかりました。分子シミュレーションっぽい条件もありましたね。次回は「整列」を加えて、本来のボイドモデルに近いシミュレーションをしたいです。
おまけ
Social Distance Ver. も置いておきます。どうぞ使ってください。

