やること
17-5ではチューリング・パターンを作ってみましたが、微分方程式アレルギーの方にはちょっと難しかったです。今回は、Youngの単純化したモデル(David A.Young, Mathematical Biosciences 72(1), 51-58, 1984)を用いて、さらにお手軽にチューリング・パターンを楽しんでみましょう。
参考文献
論文はこちらです。
単純化したチューリングモデルについてはこちらの「セルオートマトンによるチューリングモデルの再現」の章もご参照ください。
こちらもご参照ください。

単純化モデル
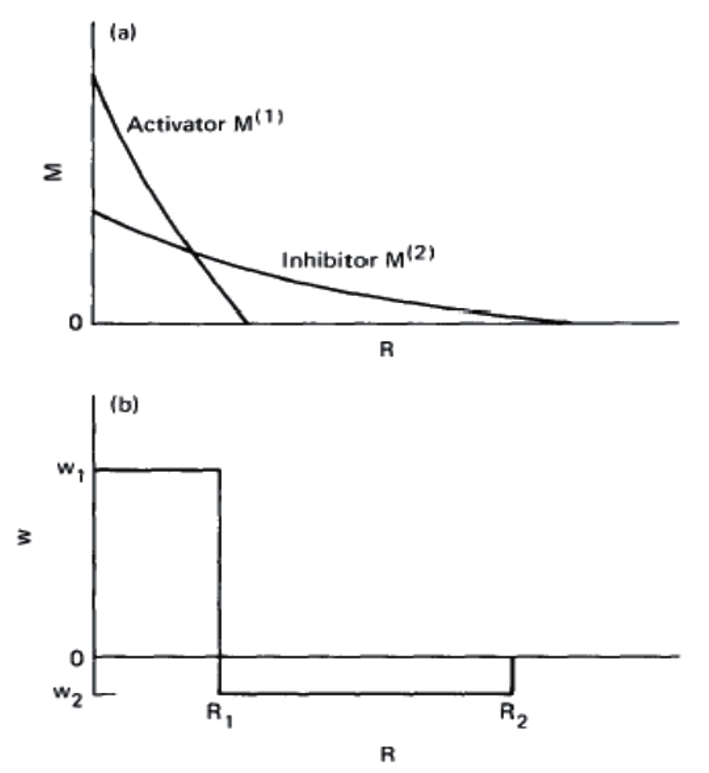
もともとのモデルは、次のような仮定に基づいていました(図・上側)。
- 2つの物質
- 周囲の2物質の濃度が影響し合う
- 2物質とも連続的な濃度(0~1)
Youngのモデルでは、次のように単純化されています(図・下側)。
- 1つの物質
- 周囲の濃度が影響する
- 離散的な濃度(0または1)
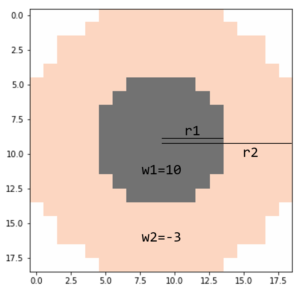
具体的には、次のような円形の畳み込みフィルタを用いて、各セルの状態を更新していきます。畳み込んだ結果が0より大きければ1(True)、0以下であれば0(False)とします。
実行環境
WinPythonかGoogle Colaboratoryを用います。
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

ソースコード
状態の更新が1行で済むってすごくないですかこのモデル。
import numpy as np
import numpy.random as nr
from scipy import signal
import matplotlib.pyplot as plt
#============================
#設定
#============================
#フィールドサイズ
h, w = 100, 100
#パラメータ
r1 = 5
r2 = 10
w1 = 10
w2 = -3.0
#終了ステップ数
max_step = 20
#============================
#メイン処理
#============================
#フィールドの初期化
#f = np.zeros((h, w), dtype=bool) #0で初期化
f = nr.randint(0, 2, (h, w), dtype=bool) #ランダムに初期化
#畳み込み用のフィルタ
g = np.zeros((r2*2 - 1, r2*2 - 1))
for i in range(len(g)):
for j in range(len(g[0])):
if (i + 1 - r2)**2 + (j + 1 - r2)**2 < r1**2:
g[i, j] = w1
if r1**2 <= (i + 1 - r2)**2 + (j + 1 - r2)**2 < r2**2:
g[i, j] = w2
#フィルタの表示
plt.imshow(g, cmap='RdGy', vmin=-15, vmax=15)
plt.show(), print()
#初期状態の表示
plt.imshow(f, cmap='binary', vmin=0, vmax=1)
#plt.savefig('save/{}.png'.format(0), bbox_inches='tight', pad_inches=0)
plt.show(), print()
#状態の更新
for i in range(1, max_step + 1):
#畳み込みとフィールドの更新、0より大きければ生存(True)、0以下であれば死(False)
f = signal.convolve2d(f, g, mode='same',boundary='wrap') >= 0
#表示
plt.imshow(f, cmap='binary', vmin=0, vmax=1)
#plt.savefig('save/{}.png'.format(i), bbox_inches='tight', pad_inches=0)
plt.show(), print()基本の条件(r1=5, r2=10)
まずは、線がメインの模様です。w1=10, w2=-3.0

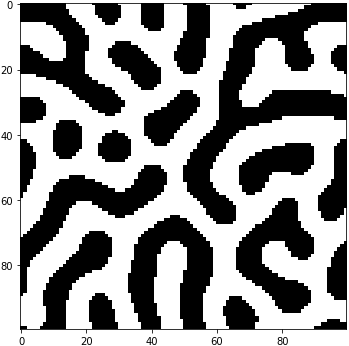
w2を上げると白玉に。w1=10, w2=-2.5

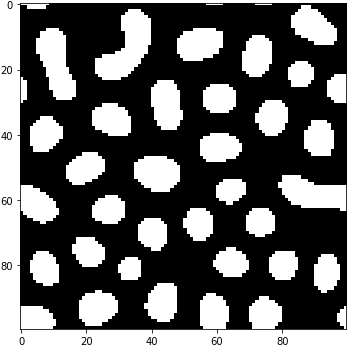
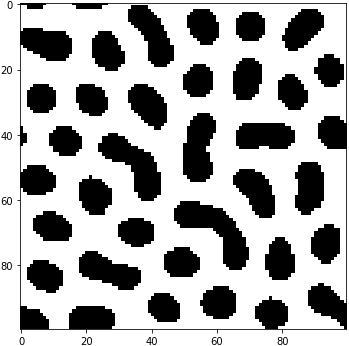
w2を下げると犬の糞黒玉に。w1=10, w2=-3.5

チューリング・パターンが出現するパラメータ条件を探索しました。
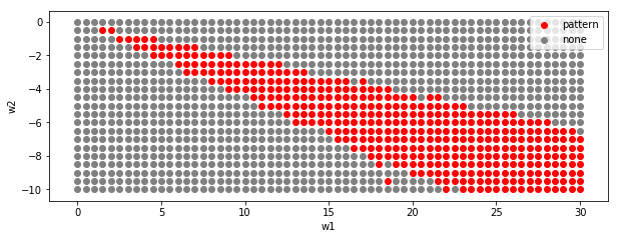
細い条件(r1=3, r2=6)
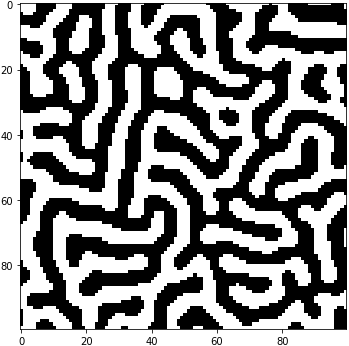
畳み込みフィルターの規模を小さくすると、影響される範囲が狭まって、パターンは細かくなるようです。w1=10, w2=-3.0

パラメータ条件は広くなりました。
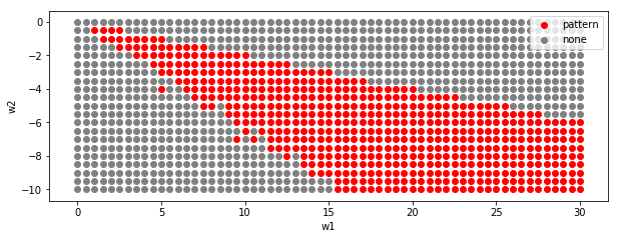
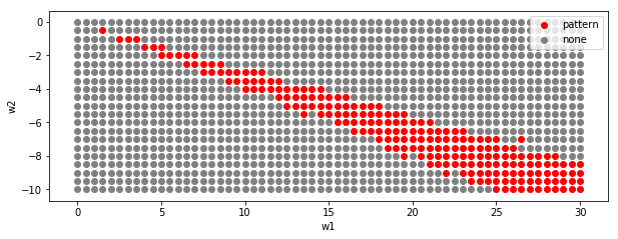
太い条件(r1=10, r2=20)
畳み込みフィルターの規模を大きくすると、パターンは太くなります。w1=10, w2=-3.2

パラメータ条件は狭くなりました。
その他の条件
r1とr2のバランスを変えると、w1, w2のパラメータ条件も変わってくるようです。
外の円を狭くしました。r1=5, r2=8
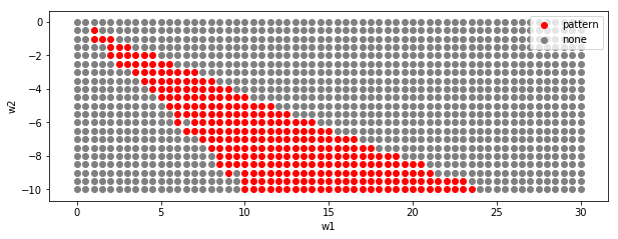
外の円を広くしました。r1=5, r2=12
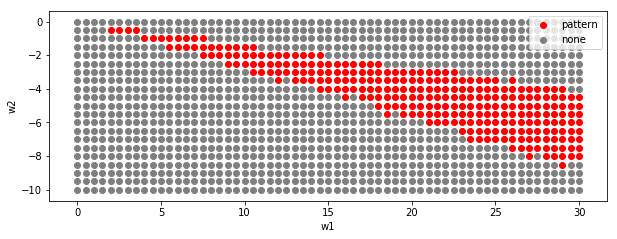
まとめ
数理モデル化とは、余計なものを取り除き、物事の本質をとらえる作業です(実はビネクラの社名もこれに由来しているとかいないとか)。これだけモデルを単純化してもチューリング・パターンが出現するのには驚かされます。


