9-9. vcoptでライフゲームの逆方向を計算してみた

GA / vcopt

2019/06/23

やること
参考文献
実行環境
ライフゲームの基本
準備
リバース計算
順方向で確認
おわりに

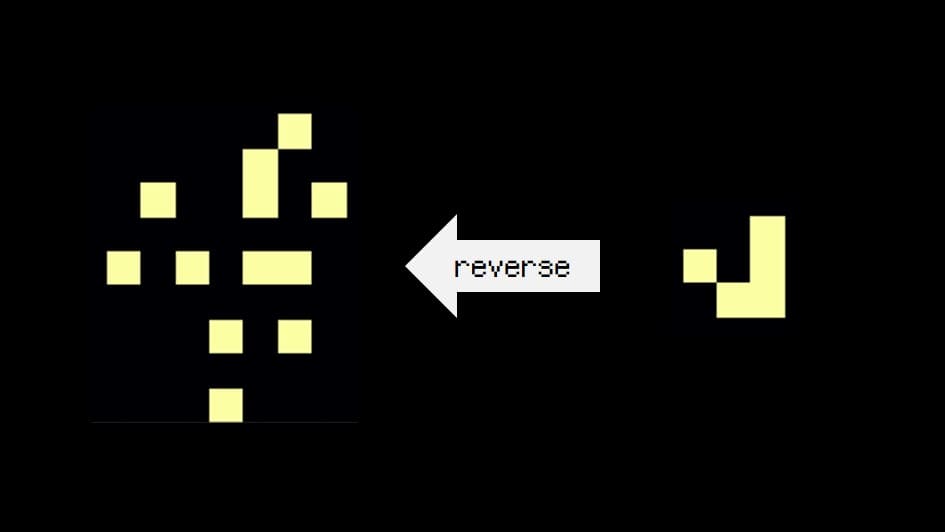
やること

※2022/11/18 コードと結果を大幅に修正しました

ライフゲームは１ステップ先を計算するのは簡単ですが、１ステップ前を計算するのはなかなか難しいです。vcoptで逆ライフゲームを試してみましょう。今回はvcopt().dcGA()を繰り返し実行するので少しトリッキーです。

参考文献

ライフゲームは、順方向の結果は一意に定まりますが、逆方向は一意ではありません。したがって、ハッシュや暗号に応用できると言われています。

https://www.jstage.jst.go.jp/article/pjsai/JSAI08/0/JSAI08_0_196/_pdf

vcoptの使い方についてはチュートリアルをご参照ください。

vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

ライフゲームの基本

こちらの記事をご参照ください。

準備

まずは設定、関数、初期化までです。

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
from vcopt import vcopt
from copy import deepcopy

#============================
#設定
#============================
#高さ、幅
h, w = 10, 10

#任意の最終状態を用意
state = np.array([[0,0,1],
                  [1,0,1],
                  [0,1,1]], dtype=int)

#フィールドのどこに置くか（左上点を指定）
p = (4, 4)


#============================
#関数
#============================
#フィールドの表示
def show(f):
    plt.figure()
    plt.imshow(f, cmap='inferno')
    plt.show(), print()

#３つのフィールドを並べて表示
def show_3(f1, f2, f3):
    plt.figure()
    plt.subplot(1, 3, 1)
    plt.imshow(f1, cmap='inferno')
    plt.title('estimated {}'.format(step))
    plt.subplot(1, 3, 2)
    plt.imshow(f2, cmap='inferno')
    plt.title('estimated {}'.format(step + 1))
    plt.subplot(1, 3, 3)
    plt.imshow(f3, cmap='inferno')
    plt.title('real {}'.format(step + 1))
    plt.show(), print()

#前方向への更新
def get_after(f):
    #周囲の生存マスを足し込む
    around = signal.convolve2d(f, g, mode='same', boundary='wrap')
    #１ステップ未来のフィールド（すべて死状態）
    f2 = np.zeros(f.shape, dtype=bool)
    #生きているマスが生きる条件（＝生存）
    f2[around*f==2] = True
    f2[around*f==3] = True
    #死んでいるマスが生きる条件（＝誕生）
    f2[around*~f==3] = True
    return f2

#生存セルに余白を付けた領域
def get_mask(f):
    #周囲の生存マスを足し込む
    around = signal.convolve2d(f, g, mode='same', boundary='wrap')
    #関与したセルのマスク
    f2 = around > 0
    return f2

#評価関数
def get_score(para):
    '''元フィールド(f_now)とマスク(mask)はグローバルを参照'''
    #paraから過去フィールドの復元
    f2 = np.zeros((h, w), dtype=bool)
    f2[mask] = para
    #更新
    f3 = get_after(f2)
    #目標との差分マス数
    diff = np.sum((f_now!=f3)**2)
    #過去の生セル比率
    l_score = np.sum(f2) / (h * w)
    return diff + l_score


#============================
#初期化
#============================
#畳み込み用のフィルタ
g = np.array([[1, 1, 1],
              [1, 0, 1],
              [1, 1, 1]], dtype=int)    

#フィールド生成
f_now = np.zeros((h, w), dtype=bool)

#初期状態
f_now[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state
show(f_now)

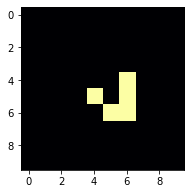
目指すべきグライダーが表示されました。

先に説明すると評価関数は少し工夫しています。あるparaからフィールドを復元し、１ステップ後を計算し、目標フィールドとの差分をdiffとします。これだけだとセルが発散しがちなので、セルがまとまりやすいように「できるだけ生存セルが少なくなるように」重みを付けています。

リバース計算

次にグライダーの逆ライフゲーム探索です。ステップは-1から-99までさかのぼっていき、1ステップ前の計算に失敗した段階でbreakします。乱数シードによって結果が異なるのでご注意ください。

#============================
#リバース計算
#============================
for step in range(-1, -100, -1):
    print('step {}'.format(step))
    #マスク取得
    mask = get_mask(f_now)
    
    #パラメータ範囲
    para_range = [[i for i in range(2)] for j in range(np.sum(mask))]
    
    #GAで過去フィールドを最適化
    para, score = vcopt().dcGA(para_range,
                               get_score,
                               0.0,
                               show_pool_func='bar', #Noneで非表示
                               max_gen=30000)
    
    #過去フィールドの復元
    f_before = np.zeros((h, w), dtype=bool)
    f_before[mask] = para
    
    #3つ並べて表示
    show_3(f_before, get_after(f_before), f_now)
    
    #終了条件
    if score > 1.0:
        print('not match'.format())
        break
    
    #次ステップに向けて入れ替え
    f_now = deepcopy(f_before)

step -1
(中略)
para = np.array([0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0])
score = 0.05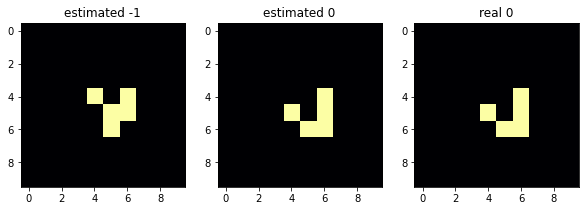

step -2
(中略)
para = np.array([0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0])
score = 0.05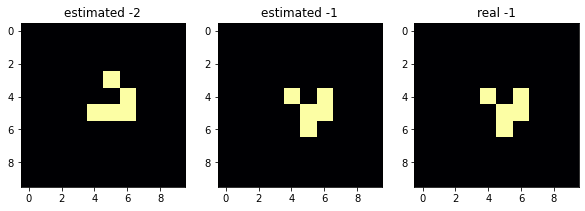

step -3
(中略)
para = np.array([0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0])
score = 0.05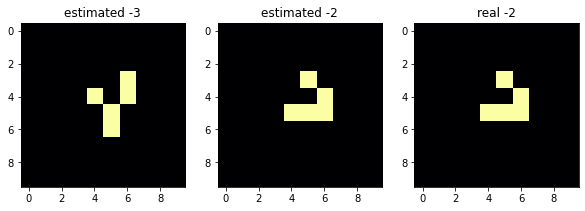

step -4
(中略)
para = np.array([0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1])
score = 0.06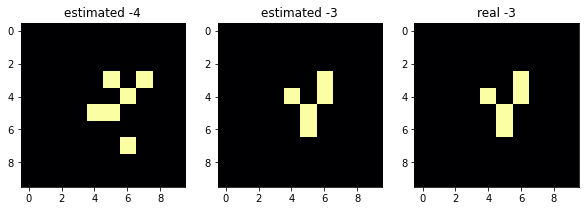

step -5
(中略)
para = np.array([0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0])
score = 0.08

step -6
(中略)
para = np.array([0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0])
score = 0.12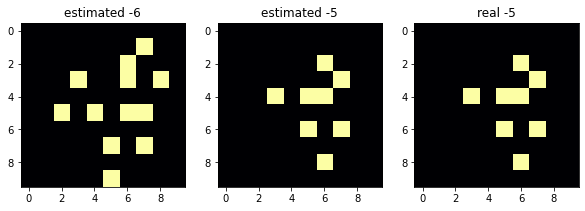

step -7
(中略)
para = np.array([1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0])
score = 2.14

not match

3連グラフは右が現在、左が計算された1ステップ前、中央がその1ステップ後です。つまり中央と右が一致していれば計算成功を意味します。スコアは1.0より小さければ計算成功です。

結果は-4ステップ目頃から発散し始め、-7ステップ目の計算に失敗しました。score=2.14というのは２マスの食い違いが生じ、フィールドの14%が生存セルという意味です。

順方向で確認

うまく計算できた-6ステップ目から再生してみます。

#============================
#順方向を確認
#============================
for i in range(step + 1, 1):
    #表示
    print('real {}'.format(i))
    show(f_now)
    
    #更新
    f_now = get_after(f_now)

real -6
real -5
real -4
real -3
real -2
real -1
real 0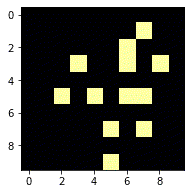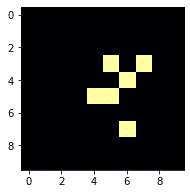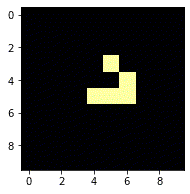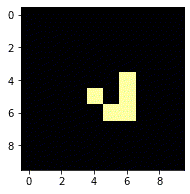

ちゃんとグライダーになりましたね。

おわりに

もっと長く過去を求めるには評価関数を工夫する必要がありそうです。暗号解読への道は遠い！