17-4. ライフゲーム（六角形、基本ルール）

人工生命 / ライフゲーム

2019/05/27

やること
参考文献
考え方（六角形の表示方法）
実行環境
ソースコード
ランダムスタートで実行してみる
雪の結晶（大）
まとめ

やること

六角形のフィールドでライフゲームに挑戦します。

参考文献

これらを参考にさせていただきました。

http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0853-10.pdf

https://blogs.yahoo.co.jp/white_rime/26019642.html

考え方（六角形の表示方法）

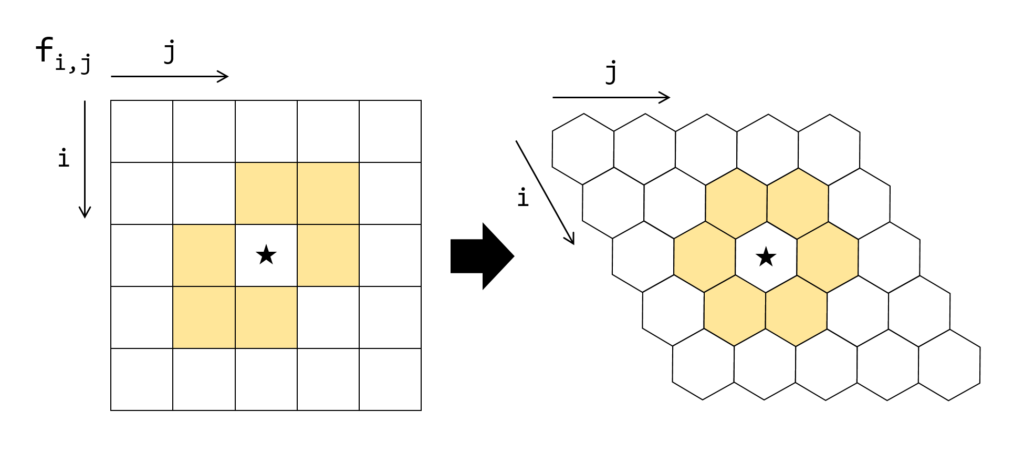
２次元配列を斜めにひねって表示することにします。よって、ステップの繰り返し計算においては、８近傍から左上と右下を除いた６近傍の状態を見ることになります。

生存ルールは245/25とします。

	次のステップでの生存条件
生存セル	隣接する８セルのうち生存セルが２、４、５個
死セル	隣接する８セルのうち生存セルが２、５個

実行環境

どちらかを用いますが、WinPythonをおすすめします。WinPythonでは図が紙芝居のようにパラパラ流れて見やすいですが、Colabではスクロールする必要があり見づらいです。

Colabにも対応しました！（推奨）

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

Google Colaboratoryが利用可能です。

Google Colab

ソースコード

やはり17-1の記事のソースコードがベースとなっています。グラフは六角形のマーカーをでっかく表示しています。周囲のマスを足し込む部分が６近傍になっていることを確認してください。

↓WinPythonコード

import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt

#============================
#初期状態の設定
#============================

#高さ、幅（同じ値にしてください）
h, w = 30, 30

#任意の状態を用意
state = nr.randint(0, 2, (4, 4))

#フィールドのどこに置くか（左上点を指定）
p = (13, 13)

#終了ステップ数
max_step = 100

#マーカーサイズ
marker_size = 130

#============================
#メイン処理
#============================

#フィールドの生成
f = np.zeros((h, w), dtype=bool)

#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state

#表示に用いるx軸とy軸の値を用意
x = np.zeros(h*w)
y = np.zeros(h*w)
for j in range(h):
    x[w*j:w*(j + 1)] = np.arange(w)+0.5*j
    y[w*j:w*(j + 1)] = np.ones(w)*j*0.866

#初期状態の表示
size = h // 5
plt.figure(figsize=(size*1.5, size*0.866))
plt.scatter(x, y, c=f.flatten(), marker='h', s=marker_size, cmap='inferno')
plt.xlim([-1, h*1.5]); plt.ylim([h*0.866, -1])
#plt.savefig('save/{}.png'.format(0), bbox_inches='tight', pad_inches=0)
plt.show(), print()

#状態の更新
for i in range(1, max_step + 1):
    
    #周囲の生存マス数を記録するための配列
    mask = np.zeros((h, w))
    
    #周囲の生存マスを足し込む
    mask[1:, :] += f[:-1, :] #上
    mask[:-1, :] += f[1:, :] #下
    mask[:, 1:] += f[:, :-1] #左
    mask[:, :-1] += f[:, 1:] #右
    mask[1:, :-1] += f[:-1, 1:] #右上
    mask[:-1, 1:] += f[1:, :-1] #左下
    
    #未来のフィールド（すべて死状態）
    future = np.zeros((h, w), dtype=bool)
    
    #生きているマスが生きる条件（＝生存）
    future[mask*f==2] = 1
    future[mask*f==4] = 1
    future[mask*f==5] = 1
    #死んでいるマスが生きる条件（＝誕生）
    future[mask*~f==2] = 1
    future[mask*~f==5] = 1
    
    #フィールドの更新（浅いコピーに注意）
    f = future
    
    #表示
    size = h // 5
    plt.figure(figsize=(size*1.5, size*0.866))
    plt.scatter(x, y, c=f.flatten(), marker='h', s=marker_size, cmap='inferno')
    plt.xlim([-1, h*1.5]); plt.ylim([h*0.866, -1])
    #plt.savefig('save/{}.png'.format(i), bbox_inches='tight', pad_inches=0)
    plt.show(), print()

↓Colabコード

import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from matplotlib import animation, rc

#============================
#初期状態の設定
#============================

#高さ、幅（同じ値にしてください）
h, w = 30, 30

#任意の状態を用意
state = nr.randint(0, 2, (4, 4))

#フィールドのどこに置くか（左上点を指定）
p = (13, 13)

#終了ステップ数
max_step = 100

#マーカーサイズ
marker_size = 130

#============================
#メイン処理
#============================

#フィールドの生成
f = np.zeros((h, w), dtype=bool)

#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state

#表示に用いるx軸とy軸の値を用意
x = np.zeros(h*w)
y = np.zeros(h*w)
for j in range(h):
    x[w*j:w*(j + 1)] = np.arange(w)+0.5*j
    y[w*j:w*(j + 1)] = np.ones(w)*j*0.866

#画像をスタックする配列の準備
size = h // 5
fig = plt.figure(figsize=(size*1.5, size*0.866))
plt.xlim([-1, h*1.5]); plt.ylim([h*0.866, -1])
ims = []

#初期状態の表示
im = plt.scatter(x, y, c=f.flatten(), marker='h', s=marker_size, cmap='inferno')
ims.append([im])

#状態の更新
for i in range(1, max_step + 1):
    
    #周囲の生存マス数を記録するための配列
    mask = np.zeros((h, w))
    
    #周囲の生存マスを足し込む
    mask[1:, :] += f[:-1, :] #上
    mask[:-1, :] += f[1:, :] #下
    mask[:, 1:] += f[:, :-1] #左
    mask[:, :-1] += f[:, 1:] #右
    mask[1:, :-1] += f[:-1, 1:] #右上
    mask[:-1, 1:] += f[1:, :-1] #左下
    
    #未来のフィールド（すべて死状態）
    future = np.zeros((h, w), dtype=bool)
    
    #生きているマスが生きる条件（＝生存）
    future[mask*f==2] = 1
    future[mask*f==4] = 1
    future[mask*f==5] = 1
    #死んでいるマスが生きる条件（＝誕生）
    future[mask*~f==2] = 1
    future[mask*~f==5] = 1
    
    #フィールドの更新（浅いコピーに注意）
    f = future
    
    #表示
    im = plt.scatter(x, y, c=f.flatten(), marker='h', s=marker_size, cmap='inferno')
    ims.append([im])
    
    
    
#アニメーション表示の準備
print('making animation......')
print('len(ims) = ' + str(len(ims)))
ani = animation.ArtistAnimation(fig, ims, interval=50, blit=True)

#ここにアニメを表示する場合はこちらを有効に
rc('animation', html='jshtml')
ani

#.gifや.mp4を保存する場合はこちらを有効に
#ani.save('aaa.gif', writer='imagemagick',fps=40)
#ani.save('bbb.mp4', writer="ffmpeg")

ランダムスタートで実行してみる

ソースコードをそのまま実行すると、４×４のランダムな状態が中心に置かれてスタートします。生き物っぽい感じがします。

雪の結晶（大）

#============================
#初期状態の設定
#============================

#高さ、幅（同じ値にしてください）
h, w = 100, 100

#任意の状態を用意
state = np.array([[0,0,0,0,0,0,1,0,0],
                   [0,0,0,0,0,1,1,0,0],
                    [0,0,1,1,0,0,0,1,1],
                     [0,0,1,0,1,1,0,1,0],
                      [0,0,0,1,0,1,0,0,0],
                       [0,1,0,1,1,0,1,0,0],
                        [1,1,0,0,0,1,1,0,0],
                         [0,0,1,1,0,0,0,0,0],
                          [0,0,1,0,0,0,0,0,0]])

#フィールドのどこに置くか（左上点を指定）
p = (46, 46)

#終了ステップ数
max_step = 180

#マーカーサイズ
marker_size = 130

出力にとても時間がかかります。下の動画は16MBくらいあるのでご注意ください。