12/9(月) 応用科学学会シンポジウムで自動運転に関する講演を担当します☆彡

20-3. 遺伝的アルゴリズム（vcopt）でライツアウトを解く

やること

ライツアウト（lights out）というパズルがあります。ライトを消せ！的な意味です。

Lights Out - confetti - Apps on Google Play
Solve addicting puzzles and celebrate with fun confetti. No Ads & works offline!
play.google.com

例題１

マスをクリックすると、そのマスを含む十字型の５マスがひっくり返ります。マスをすべて消灯させればクリアです。

解答は一意に定まりませんが、最少手数の答えがこちらです。

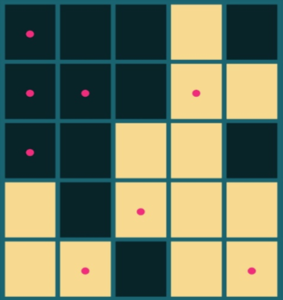
同じマスを２回以上クリックすることには意味がないため、各マスとも「１回クリックする」か「クリックしない」の２択しかありません。よって解の組み合わせは225＝約3000万通りあります。

今日は、このパズルをGA（遺伝的アルゴリズム）を用いて解いてみます。

解法

解の一つを見つける方法はこちらをご参照ください。5*5サイズは特別に難しいそうです。

ライツアウト攻略！ - 人生ってそういうものなんだと思います
katsubi.blog.fc2.com
301 Moved Permanently
www.ic-net.or.jp
Puzzle DE Programming / ライツアウトの解法
Puzzle,パズル,プログラミング,解法
www.nct9.ne.jp

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
sourceforge.net

vcoptの使い方についてはチュートリアルをご参照ください。

お手軽最適化パッケージ「vcopt」チュートリアル
実行環境Windowsマシンで実行する方にはWinPython3.6をおすすめしています。インストール不要で、USBメモリに入れて持ち運ぶこともできます。...
vigne-cla.com
2019/09/23

vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。

お手軽最適化パッケージ「vcopt」仕様書
はじめにvcoptとは遺伝的アルゴリズム（Genetic Algorithm, GA）による本格的な組合せ最適化がお手軽にできる無料のPythonパッケージで...
vigne-cla.com
2019/09/22

考え方

長さ25の遺伝子配列を用意し、各遺伝子は０か１をとることにします。これを5*5の２次元配列にリサイズし、１をクリックするマスとしてプレイします。

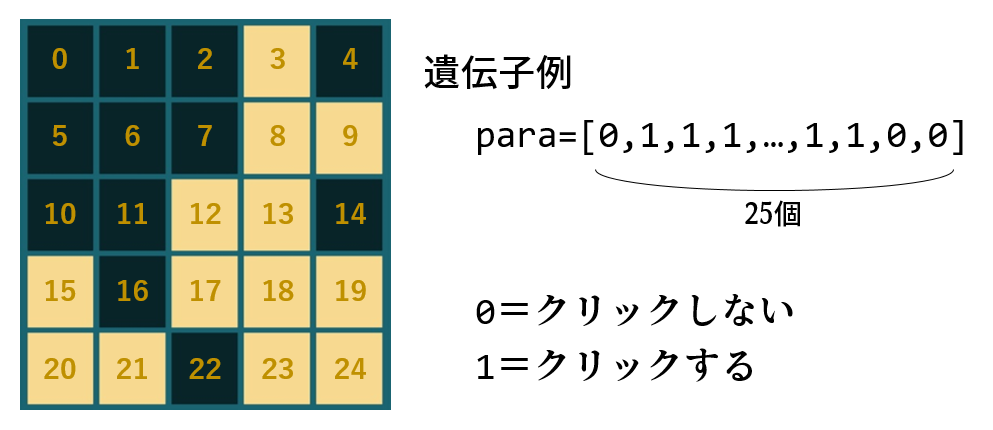
評価関数では、プレイ後の盤面を見て「点灯しているマス（＝１のマス）」の総数を返すことにします。このスコアが０に近づくように最適化を行います。

pip, import

まだvcoptをpipしていない場合はpipします。

pip install vcopt

必要なパッケージをimportします。

import numpy as np
import numpy.random as nr
from copy import deepcopy
from vcopt import vcopt

パズル問題

パズル問題は ‘-‘ と ‘#’ で表現します。’#’が点灯しているマスです。

#============================
# パズルの記述
#============================
lights = ['---#-',
          '---##',
          '--##-',
          '#-###',
          '##-##']

前処理でnumpy配列に変換し、パズルのサイズを取得します。

#============================
# パズルの変換
#============================
#変換
lights_tmp = []
for line in lights:
    line = line.replace('-', '0')
    line = line.replace('#', '1')
    lights_tmp.append(list(line))
lights = np.array(lights_tmp, dtype=int)
print('lights\n{}'.format(lights))

#サイズ
h, w = lights.shape
print('h, w\n{}, {}'.format(h, w ))
lights
[[0 0 0 1 0]
 [0 0 0 1 1]
 [0 0 1 1 0]
 [1 0 1 1 1]
 [1 1 0 1 1]]
h, w
5, 5

プレイする関数

答え盤面（クリックするマス）を入力してパズルをプレイし、結果の盤面を返す関数を作ります。

#============================
# パズルをプレイする関数
#============================
#答えにしたがってプレイする関数
def play(lights, ans):
    #盤面をコピー
    lights_copy = deepcopy(lights)
    
    #盤面に対して答えを十字型に足し込む
    lights_copy[:, :] += ans[:, :]
    lights_copy[1:, :] += ans[:-1, :]
    lights_copy[:-1, :] += ans[1:, :]
    lights_copy[:, 1:] += ans[:, :-1]
    lights_copy[:, :-1] += ans[:, 1:]
    
    #偶数回返されたマスは０、奇数回は１とする
    lights_copy = lights_copy % 2
    
    return lights_copy

#適当な答えを生成（１：クリックするマス）
ans = nr.randint(0, 2, (h, w))
print('ans:\n{}'.format(ans))

#適当な答えでプレイ
result = play(lights, ans)
print('result:\n{}'.format(result))
ans:
[[0 1 1 0 1]
 [1 1 1 1 1]
 [1 0 0 1 0]
 [0 0 0 0 1]
 [0 1 1 0 0]]
result:
[[0 1 1 0 0]
 [1 0 0 1 0]
 [0 0 1 1 1]
 [0 1 0 1 0]
 [0 1 0 0 0]]

適当な答え盤面を生成してプレイしてみると、10マスが点灯している状態になりました。

評価関数

遺伝子配列（para）を入力し、これを答え盤面に変換してパズルをプレイし、プレイ後の点灯数を返す関数を作ります。途中経過が気になる方はコメントアウトを解除して詳しく見てみてください。

#============================
# 評価関数
#============================
def lights_score(para):
    #paraを答え盤面に変形
    ans = para.reshape((h, w))
    #print('ans:\n{}'.format(ans))
    
    #それでプレイ
    result = play(lights, ans)
    #print('result:\n{}'.format(result))
    
    #点灯マス（＝１）の総数をスコアとして返す
    return np.sum(result)

#適当なparaを生成
para = nr.randint(0, 2, h*w)
print('para:\n{}'.format(para))

#適当なparaでプレイしてスコアを返す（）
score = lights_score(para)
print('score:\n{}'.format(score))
para:
[1 1 1 1 0 1 0 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 1 0 1]
score:
13

適当なparaを生成して入れたところ、スコア（残り点灯数）＝13が返ってきました。

GAで最適化

離散的なGAができる vcopt().dcGA() を用います。para_range は各遺伝子が取り得る [0, 1] という選択肢が25個並んだ２次元配列です。評価値は０を目指します。

#===============================================
# GA
#===============================================
#パラメータ範囲
para_range = [[0, 1] for _ in range(h*w)]
print('para_range:\n{}'.format(para_range))

#GAで最適化
para, score = vcopt().dcGA(para_range,             #パラメータ範囲
                           lights_score,           #評価関数
                           0,                      #目標値
                           pool_num=h*w*50,        #個体数を通常の5倍に増やす
                           show_pool_func='print') #簡易出力機能を使う


#結果の確認
ans = para.reshape((h, w))
print('ans:\n{}'.format(ans))

result = play(lights, ans)
print('result:\n{}'.format(result))
para_range:
[[0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1]]
___________________ info ___________________
para_range : n=25
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 1250
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 1250/1250        
gen=0, best_score=4.0, mean_score=12.4656, mean_gap=12.4656, time=0.4
gen=1250, best_score=4.0, mean_score=10.2448, mean_gap=10.2448, time=0.9
gen=2500, best_score=4.0, mean_score=9.168, mean_gap=9.168, time=1.3
・・・
gen=47500, best_score=1.0, mean_score=3.9704, mean_gap=3.9704, time=13.0
gen=48750, best_score=1.0, mean_score=3.9256, mean_gap=3.9256, time=13.3
gen=50000, best_score=0.0, mean_score=3.8672, mean_gap=3.8672, time=13.7
__________________ results _________________
para : [0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 1 1 0 0]
score : 0.0
____________________ end ___________________
ans:
[[0 0 1 0 1]
 [0 1 1 1 1]
 [1 0 0 0 0]
 [1 0 0 0 1]
 [1 1 1 0 0]]
result:
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
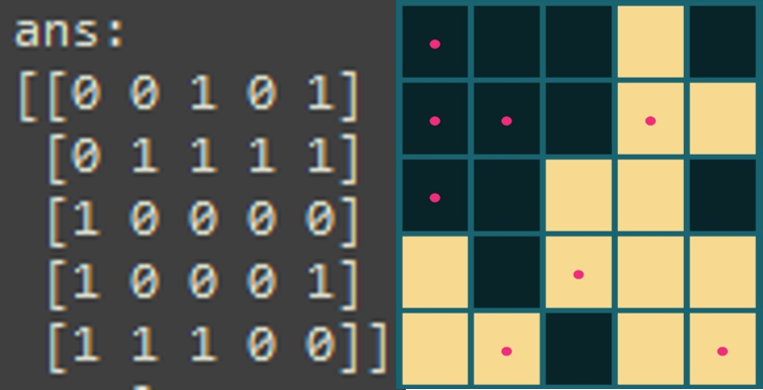
 [0 0 0 0 0]]

14秒でスコア０が見つかりました。このように11マスをクリックするとすべて消灯しますが、どうやら最短の解ではないようです。（赤い点が最短の解です）

評価関数の工夫

評価関数において、点灯マスの総数を１の位、クリックしたマスの総数を0.1の位とする小数を返すように修正しました。例えばスコア＝0.5は、すべてのマスが消灯しており、クリック数が５であることを意味します。

#============================
# 評価関数
#============================
def lights_score(para):
    #paraを答え盤面に変形
    ans = para.reshape((h, w))
    #print('ans:\n{}'.format(ans))
    
    #それでプレイ
    result = play(lights, ans)
    #print('result:\n{}'.format(result))
    
    #点灯マス（＝１）の総数を１の位、クリックしたマスの総数を0.1の位としてスコアを返す
    return np.sum(result) + 0.1 * np.sum(ans)
para_range:
[[0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1], [0, 1]]
___________________ info ___________________
para_range : n=25
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 1250
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 1250/1250        
gen=0, best_score=6.2, mean_score=13.7808, mean_gap=13.7808, time=0.5
gen=1250, best_score=5.2, mean_score=11.4683, mean_gap=11.4683, time=0.9
gen=2500, best_score=4.2, mean_score=10.3748, mean_gap=10.3748, time=1.4
・・・
gen=48750, best_score=1.2, mean_score=4.7123, mean_gap=4.7123, time=16.1
gen=50000, best_score=1.2, mean_score=4.6365, mean_gap=4.6365, time=16.6
gen=51250, best_score=0.8, mean_score=4.563, mean_gap=4.563, time=17.0
gen=52500, best_score=0.8, mean_score=4.4944, mean_gap=4.4944, time=17.4
・・・
gen=168750, best_score=0.8, mean_score=0.8496, mean_gap=0.8496, time=53.8
gen=170000, best_score=0.8, mean_score=0.8474, mean_gap=0.8474, time=54.2
gen=171250, best_score=0.8, mean_score=0.8474, mean_gap=0.8474, time=54.6
__________________ results _________________
para : [1 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1]
score : 0.8
____________________ end ___________________
ans:
[[1 0 0 0 0]
 [1 1 0 1 0]
 [1 0 0 0 0]
 [0 0 1 0 0]
 [0 1 0 0 1]]
result:
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
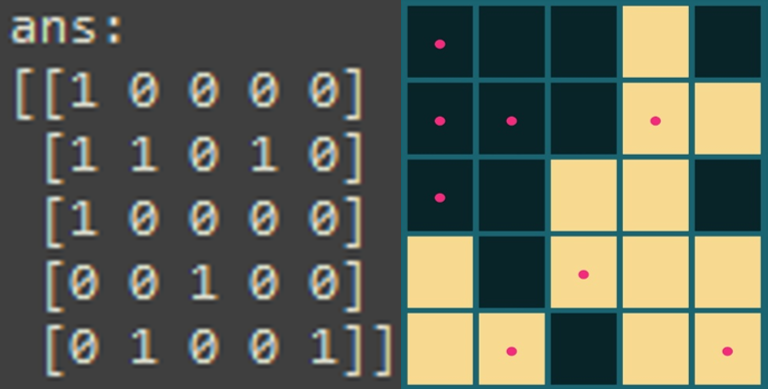
 [0 0 0 0 0]]

収束に55秒かかりましたが、17秒で最少手数の解を見つけました。

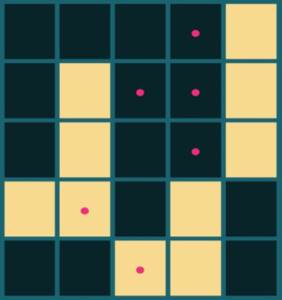
例題２

こちらの問題もなかなか難しいです。「え、そこクリックするの？」という感じです。

#============================
# パズルの記述
#============================
lights = ['----#',
          '-#--#',
          '-#--#',
          '##-#-',
          '--##-']
___________________ info ___________________
para_range : n=25
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 1250
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 1250/1250        
gen=0, best_score=4.7, mean_score=13.7857, mean_gap=13.7857, time=0.5
gen=1250, best_score=4.7, mean_score=11.3924, mean_gap=11.3924, time=1.0
gen=2500, best_score=3.8, mean_score=10.2861, mean_gap=10.2861, time=1.4
・・・
gen=21250, best_score=3.1, mean_score=6.6331, mean_gap=6.6331, time=7.5
gen=22500, best_score=3.1, mean_score=6.5265, mean_gap=6.5265, time=8.2
gen=23750, best_score=0.6, mean_score=6.4251, mean_gap=6.4251, time=8.5
gen=25000, best_score=0.6, mean_score=6.325, mean_gap=6.325, time=8.9
・・・
gen=153750, best_score=0.6, mean_score=0.7071, mean_gap=0.7071, time=49.4
gen=155000, best_score=0.6, mean_score=0.7024, mean_gap=0.7024, time=49.9
gen=156250, best_score=0.6, mean_score=0.7024, mean_gap=0.7024, time=50.4
__________________ results _________________
para : [0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0]
score : 0.6000000000000001
____________________ end ___________________
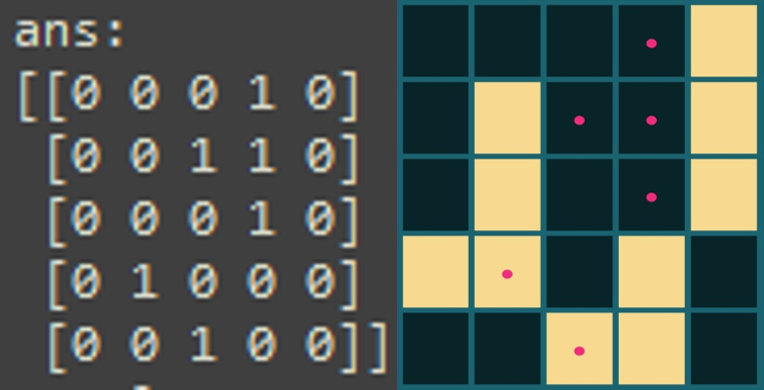
ans:
[[0 0 0 1 0]
 [0 0 1 1 0]
 [0 0 0 1 0]
 [0 1 0 0 0]
 [0 0 1 0 0]]
result:
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]]

８秒で最少手数が見つかり、50秒で収束しました。ちなみに、事前にクリック数が分かっていれば８秒で止めることも可能です。

感想

一つの解を見つけるのはさほど難しくありません（解法の記事を参照ください）。しかし、最小手数の解を見つけるのは大変です。今回はGAの威力が発揮できたのではないでしょうか。（え、このサイズなら全探索のほうが早いだろうって？聞こえないですｱｰｱｰ）

SNS等でお気軽にご連絡ください

※当ブログに関することは何でもご相談・ご依頼可能です（Servicesになくても）
※TwitterはFF外の場合はDMではなく返信orメンションでお願いしますm(_ _)m

情報発信しています

Twitterを見る
Youtubeを見る

質問・コメントはSlackやDiscordでお気軽に

Slack「AI FASHION」に参加

勉強会の告知はこちらで

connpass「AI FASHION」
GA / vcopt
vcopt パズル 最適化
この記事を書いた人

博士（理学）。専門は免疫細胞、数理モデル、シミュレーション。米国、中国で研究に携わった。遺伝的アルゴリズム信者。物価上昇のため半額弁当とともに絶滅寸前。

この記事をシェアする
Yasuda
Vignette & Clarity（ビネット＆クラリティ）
タイトルとURLをコピーしました