やること
組合せ最適化の基本問題として「最大カット問題(Max cut問題)」がありますが、これがなんとも分かり辛いです。量子アニーリングの基本問題としても頻繁に取り上げられますが、どうしても理解できないという声を聞きます。
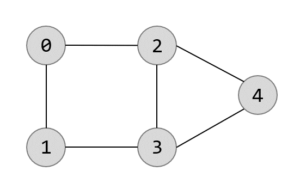
今回は最大カット問題(Max cut問題)を易しく言い換えて理解し、QUBO化して量子アニーリング(疑似アニーリング)で解いてみましょう。
何が分かりづらいか?
多くのサイトでは「できるだけ多くの線を切る」と説明され、次のような解答が示されています。
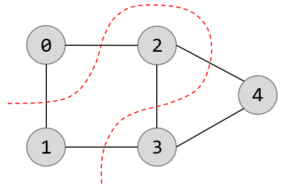
しかし疑問が残ります。もう一個切れるよね?と
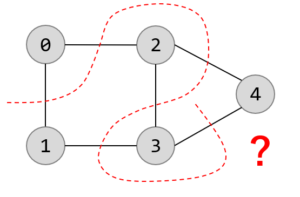
でもこれは不正解だそうです。なぜでしょうか?問題の説明が不十分なのが原因ですが、そもそもグラフ構造を使って抽象的に説明しようとするから混乱を招くのです。「一筆書きで」というのも混乱します。
参考文献
この問題をめちゃくちゃ分かりやすく言い換えている資料があります。言い換えているというか本来はこっちの意味ではないかと思いますが。。
元は内閣府革新的研究開発推進プログラム(ImPACT)による国産のコヒーレントイジングマシン「QNNCloud」(当初は量子コンピュータと呼んでいたが後に内閣府は量子コンピュータと呼ばないことを発表)に関連する説明資料のようですが、オリジナルのリンクが見つからなかったため転載サイトを引用させていただきます。申し訳ありません。

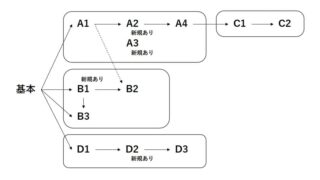
また、おさらいとして、量子アニーリングでは「n個の量子ビットからm個を1にする」という条件設定が使えることを思い出してください。これは基本の条件設定です。その他の設定可能な条件式も気になる方は過去のまとめ記事をご参照ください。
最大カット問題の言い換え
このように言い換えます。
5人の幼稚園児を2台のバスに乗せます。友達関係をできるだけ壊すように振り分けるには、どのようにグループ分けしたら良いでしょうか?
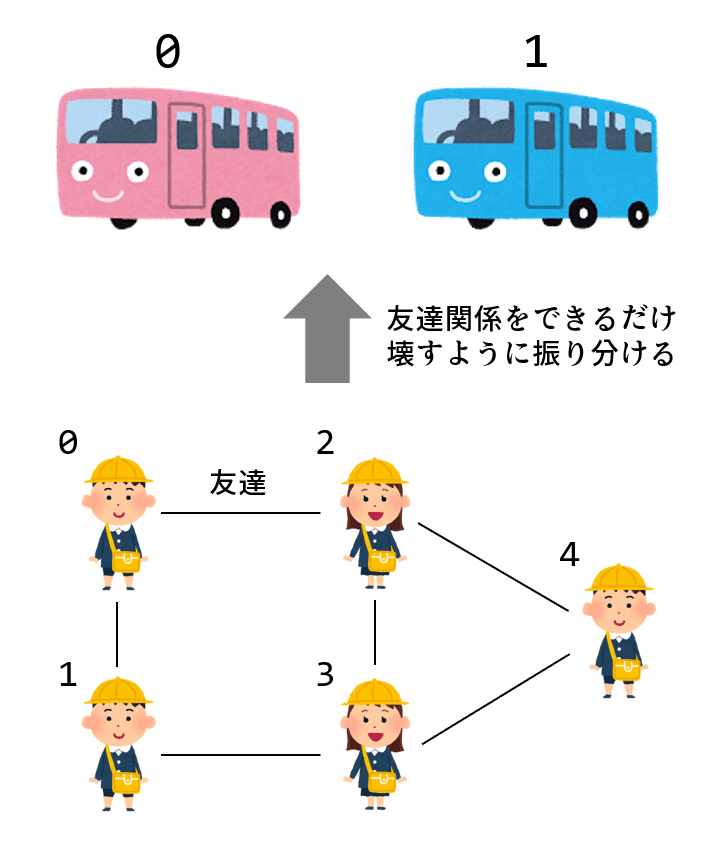
すごく分かりやすいですよね?
量子アニーリング(QUBO)での条件設定
5人の幼稚園児を5個の量子ビットに対応させます。
ある友達関係の2人に着目したとき、彼らを違うバスに乗せたいということは、彼らの量子ビットを0, 1逆にしたいということで、さらに言い換えると「2個の量子ビットから1個を1にしたい」と同じです。これをすべての友達関係で設定します。友達カットは必ずしもすべてが叶うとは限らないですが、できるだけ多くカットされるグループ分けが得られます。
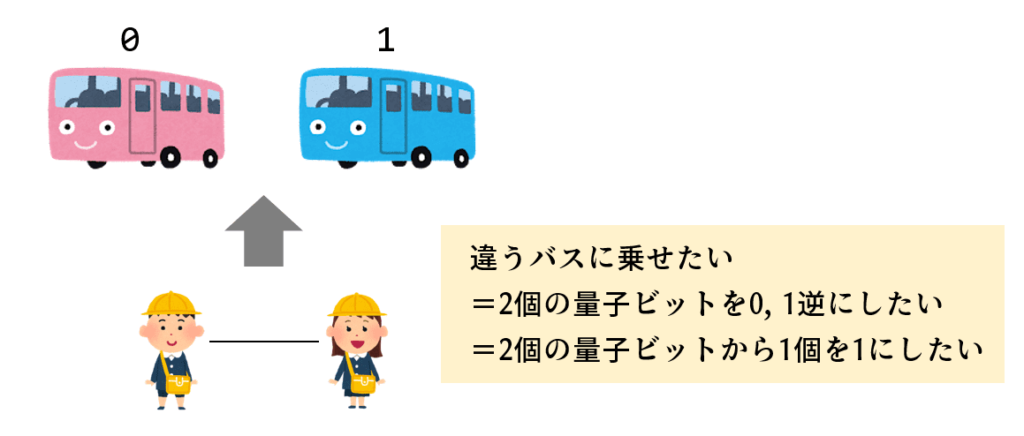
今回は友達関係の強さに差がなく、どの線も同じ重みです。「こっちを1本切ってあっちを1本残す」と「あっちを1本切ってこっちを1本残す」は同じエネルギーになるため、結果的に「できるだけ多くの本数を切る」が実現できることになります。もし友情に差があればそれに応じた係数をかける必要があり、「こっちを2本切ってあっちを1本残そう」といったことも起こり得ます。
コード
こちらです。
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
q0 = Binary('q0')
q1 = Binary('q1')
q2 = Binary('q2')
q3 = Binary('q3')
q4 = Binary('q4')
#友達関係において、違うバスに乗せたい(=2個の量子ビットを0,1逆にしたい)(=2個の量子ビットから1個を1にしたい)
H = 0
H += (q0 + q1 - 1)**2
H += (q0 + q2 - 1)**2
H += (q1 + q3 - 1)**2
H += (q2 + q3 - 1)**2
H += (q2 + q4 - 1)**2
H += (q3 + q4 - 1)**2
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')response
Sample:[0, 1, 1, 0, 0] Energy:-5.0 Occurrence:142
Sample:[1, 0, 0, 1, 0] Energy:-5.0 Occurrence:117
Sample:[0, 1, 1, 0, 1] Energy:-5.0 Occurrence:129
Sample:[1, 0, 0, 1, 1] Energy:-5.0 Occurrence:1134種類の最適解が得られましたが、実質2パターンです。一方は冒頭の模範解答と一致していて、もう一方は別解です。
エネルギーが-5になったことについて。まずオフセットで-6されていて、各条件式は叶うと+0、叶わないと+1です。つまり、5式が叶って1式が叶わなかった(5本切れて1本残った)ことを意味します。このあたりの理論はどこかでちゃんと解説する機会があればと思います。
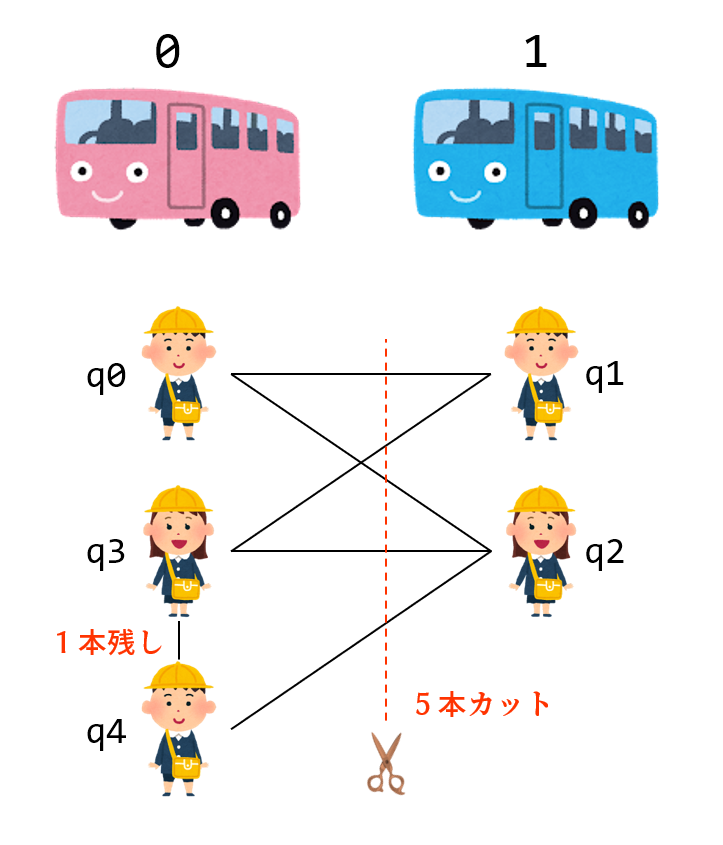
さいごに
最大カット問題、もう怖くない!