やること
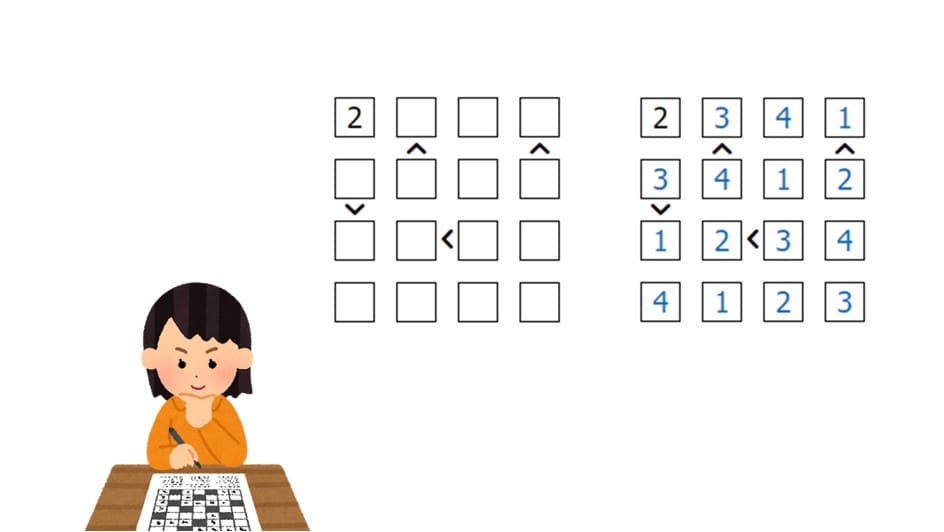
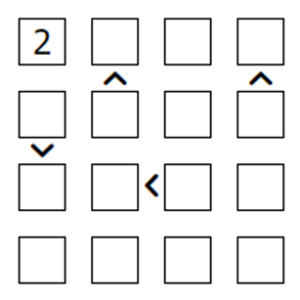
ナンバープレース(数独)はご存知ですよね。各行、各列で重複が起きないように数字を埋めるパズルです。それに不等号のルールを加えた不等号ナンプレというのもあります。
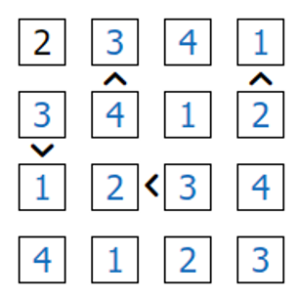
答えはこちらです。
今回はQUBOでナンプレと不等号ナンプレを解いてみます。QUBOでナンプレを解く方法はもう有名なので、発展形として不等号ナンプレも含めました。
考え方
ナンプレでは整数値を扱うためOne-hot表現を用いて、すでに記入されている数字については基本の条件設定「n個の量子ビットからm個を1にする」を使用します。
例)ある量子ビットを1にする(=1個の量子ビットから1個を1にする)
H = (q0 - 1)**2また、不等号ナンプレでは「2個の量子ビットが同時に1になったら報酬を与える」を使います。
例)2個の量子ビットが同時に1になったら報酬を与える
H = -(q0 * q1)条件式については過去のまとめ記事をご参照ください↓
どうやって解くのか?
通常のナンプレの解き方
4×4のナンプレでは4×4×4=64個の量子ビットを用意します。4個セットで一つの数字を表すワンホット表現とし、次のように3次元的な配置を想像してください。今回、混乱を避けるために量子ビット名を1始まりにしていることにご注意ください。例えば、q112は1行目1列目のワンホット2番です。これが1であればそのマスの数字は2となります。
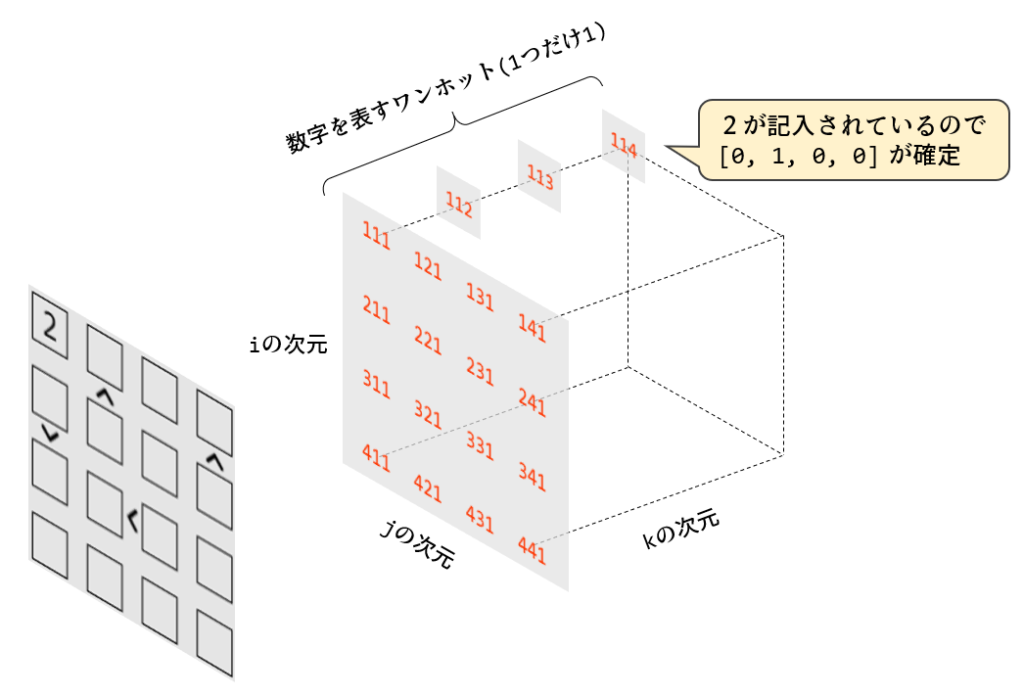
まずワンホットの設定として、「各ワンホット(kの次元)は1つだけ1になる」を16回設定します。あとは、「各行(jの次元)は1つだけ1になる」を16回、「各列(iの次元)は1つだけ1になる」を16回設定すれば「各行、各列の数字が重複しない」となり通常のナンプレが解けます。
このままでは解がたくさん出ますが、すでに記入されている数字のワンホット部分を追加指定してやれば解が絞れます(多くの問題は解が一意に定まるように作られているので最適化1つに絞れるはず)。
不等号ナンプレの解き方
不等号ナンプレではさらに条件設定を追加します。不等号関係にある量子ビット8個に着目します。
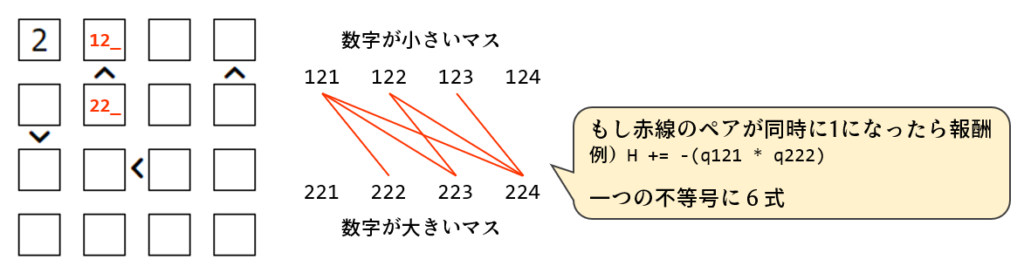
小も大もワンホットなので1つだけ1が立ちますが、大の方はより右側のビットが立たなければいけません。ですから、「赤線のペアが同時に1になったときに報酬を与える」という設定でそれを促してやります。赤線のペアは6パターンあるので6式必要です。
コード(通常のナンプレ)
まずは左上マスを2で固定するだけのナンプレです。式が多いためfor文を使っていて分かり辛いかもしれません。式はprintされるのでコンソールもご確認を。
import numpy as np
from pyqubo import Binary
from dwave_qbsolv import QBSolv
#量子ビットを用意する
#1始まり!!!!!!!!!!!!!!!
for i in range(1, 5):
for j in range(1, 5):
for k in range(1, 5):
command = f'q{i}{j}{k} = Binary(\'q{i}{j}{k}\')'
print(command)
exec(command)
#各マスはワンホットで一つだけ1になる(kの次元のワンホット)
H = 0
for i in range(1, 5):
for j in range(1, 5):
command = f'H += (q{i}{j}1 + q{i}{j}2 + q{i}{j}3 + q{i}{j}4 - 1)**2'
print(command)
exec(command)
#各行で数字が重複しない(つまり各行は一つだけ1になる)(jの次元のワンホット)
for i in range(1, 5):
for k in range(1, 5):
command = f'H += (q{i}1{k} + q{i}2{k} + q{i}3{k} + q{i}4{k} - 1)**2'
print(command)
exec(command)
#各列で数字が重複しない(つまり各列は一つだけ1になる)(iの次元のワンホット)
for j in range(1, 5):
for k in range(1, 5):
command = f'H += (q1{j}{k} + q2{j}{k} + q3{j}{k} + q4{j}{k} - 1)**2'
print(command)
exec(command)
#数字指定のマス
H += (q112 - 1)**2
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)
#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
#ワンホットから整数に戻して確認
box = np.array(list(sample.values())).reshape(4, 4, 4)
ans = np.zeros((4, 4), int)
for i in range(4):
for j in range(4):
ans[i, j] = np.argmax(box[i, j, :]) + 1
print(ans)response
Sample:[0, 1, 0,...,0, 0, 1] Energy:-49.0 Occurrence:3
[[2 3 4 1]
[1 4 2 3]
[4 1 3 2]
[3 2 1 4]]
Sample:[0, 1, 0,...,0, 0, 1] Energy:-49.0 Occurrence:2
[[2 3 4 1]
[3 4 1 2]
[4 1 2 3]
[1 2 3 4]]
Sample:[0, 1, 0,...,0, 0, 1] Energy:-49.0 Occurrence:1
[[2 4 3 1]
[1 3 4 2]
[4 2 1 3]
[3 1 2 4]]これで左上が2で固定された解がたくさん得られました。
コード(不等号ナンプレ)
さあ、不等号の設定を追加してみましょう。一つの不等号に6式、それが4箇所です。
#不等号
H += -(q121 * q222)
H += -(q121 * q223)
H += -(q121 * q224)
H += -(q122 * q223)
H += -(q122 * q224)
H += -(q123 * q224)
H += -(q141 * q242)
H += -(q141 * q243)
H += -(q141 * q244)
H += -(q142 * q243)
H += -(q142 * q244)
H += -(q143 * q244)
H += -(q311 * q212)
H += -(q311 * q213)
H += -(q311 * q214)
H += -(q312 * q213)
H += -(q312 * q214)
H += -(q313 * q214)
H += -(q321 * q332)
H += -(q321 * q333)
H += -(q321 * q334)
H += -(q322 * q333)
H += -(q322 * q334)
H += -(q323 * q334)response
Sample:[0, 1, 0,..,0, 1, 0] Energy:-53.0 Occurrence:80
[[2 3 4 1]
[3 4 1 2]
[1 2 3 4]
[4 1 2 3]]
Sample:[0, 1, 0,..,0, 0, 0] Energy:-52.0 Occurrence:2
[[2 1 3 4]
[4 2 1 3]
[1 3 4 2]
[3 4 2 1]]
Sample:[0, 1, 0,..,0, 0, 0] Energy:-52.0 Occurrence:1
[[2 1 3 4]
[3 4 1 2]
[1 2 4 3]
[4 3 2 1]]最適解は一つで、模範解答と一致しました。

【補足】今回は条件設定に重みの差をつけませんでした。重みは「優先したいこと」がある場合につけます。今回はすべての設定(願い)が叶う解が存在することがわかっているので重みを付ける必要がありません。
さいごに
ナンプレ(数独)とその亜種である不等号ナンプレが解けました。ただ、9×9のナンプレだと量子ビットが729個必要なのでアニーリングがうまくいくか分かりません。