やること
2024/09/07追記
試験問題の役割を終えたため解答の一例を公開しました。
ここ数ヶ月、QUBOでやたらにペンシルパズルを解いてきました。お楽しみいただけたでしょうか?
実は少し前に「TYTAN」というOSSのアニーリングSDKが立ち上がりました。
筆者はそのトレーニングを担当していて、ここの記事から学習に良さそうなものを選別してチュートリアルコースを組んでいます。discordコミュニティもあるので気軽に質問できます。(discord参加リンクはリンク内に↓)。
チュートリアルを終えて試験に合格するとblueqat社が認定する「qubomaster」という資格が与えられます。合格基準は、TYTANが使いこなせ、QUBO関連の受託業務を請けられるレベルと認められることです。qubomasterになると(blueqatサイト上で)認定バッジが付与され、有償業務の受託可能者リストに入ります。
今回は「qubomaster」認定試験に用いられる実力テスト1を用意しました。答えは公開していません。認定試験として挑戦する場合は別途その指示に従ってください。
おさらい
QUBOで設定できる条件式についてはこちらの記事にまとめてあります。暗記する必要はありませんが概要は把握しておくと良さそうです。
これまでのQUBOアニーリング系の記事はサイドバーの「カテゴリ一覧」→「量子コンピュータ」から絞れます。
実力テスト問題1
スターバトル(Star Battle)と呼ばれるパズルを解いてください。
例題と解答はこちらです。
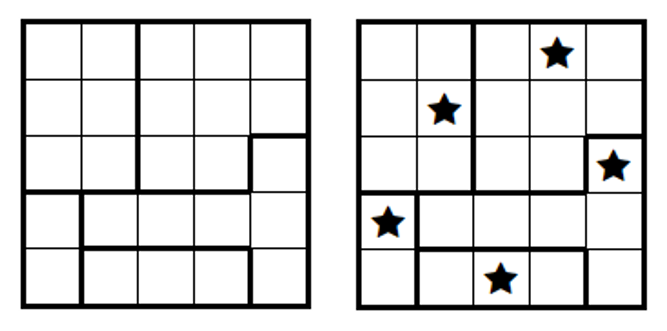
パズルのルール
- 5つの領域に各1つだけ星を置く
- 各行、各列には星が2つ以上あってはならない
- 星の8近傍に他の星があってはならない
ブラウザ上で遊んでみたいという方はPuzzle Teamさんのサイト(puzzle-loop.com)をお試しください。

それでは、実力テスト問題はこちらです。

提出方法、注意事項など
解答は、そのまま実行するだけのpythonコードを「.py」または「.ipynb」のファイル形式で以下フォームから提出してください。すぐに自動返信メールが届きます。
※100KBまでの.py, .ipynbファイルのみ受け付けます
※受付完了メールが自動送信されます
▼注意事項
- テキスト欄やコメントアウトにより最低限の説明や思考過程を含めてください
- その際、チュートリアルの「おすすめコース」のどれと関連があるかにも触れてください
- 説明のための図は必ずしも必要ありません
- アニーリングのソルバーには必ずTYTANパッケージを使用してください
- 必ずしも1回の実行で正解が得られる必要はなく、正解が得られることが期待できるコードであれば問題ありません
▼合格条件
- QUBO条件式が妥当であること
- 説明や思考過程が妥当であること
- 十分な可読性のPythonコードであること
- チュートリアル「おすすめコース」を把握していること
解答の一例(2024/09/07追記)
パズルのルールを正確に式で表現する。
pip install tytanfrom tytan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットを用意する
q = symbols_list([5, 5], 'q{}_{}')
print(q)
#各行に星は0個または1個(解釈して「必ず1個」としても良い)
Hconst1 = 0
for i in range(5):
Hconst1 += (sum(q[i, :]) - 0.5)**2
#各列に星は0個または1個(解釈して「必ず1個」としても良い)
Hconst2 = 0
for j in range(5):
Hconst2 += (sum(q[:, j]) - 0.5)**2
#領域内に星は一つだけ(一つ一つ丁寧に書いても良い)
Hconst3 = 0
Hconst3 += (np.sum(q[:3, :2]) - q[2, 0] - 1)**2
Hconst3 += (np.sum(q[:3, 2]) - 1)**2
Hconst3 += (np.sum(q[:, 3:]) - q[4, 3] - 1)**2
Hconst3 += (np.sum(q[2:, 0]) - 1)**2
Hconst3 += (np.sum(q[3:, 1:4]) - q[3, 3] - 1)**2
#星の8近傍に他の星がない(どこの2×2をとっても星は0個または1個)(他にも様々な設定方法あり)
Hconst4 = 0
for i in range(4):
for j in range(4):
Hconst4 += (np.sum(q[i:i+2, j:j+2]) - 0.5)**2
#合体
H = Hconst1 + Hconst2 + Hconst3 + Hconst4
#コンパイル
qubo, offset = Compile(H).get_qubo()
print(f'offset = {offset}')
#サンプラー選択
solver = sampler.SASampler()
#サンプリング
result = solver.run(qubo, shots=100)
#上位3件
for r in result[:3]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#画像で取得
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(1, 1))
plt.imshow(img)
plt.show()[[q0_0 q0_1 q0_2 q0_3 q0_4]
[q1_0 q1_1 q1_2 q1_3 q1_4]
[q2_0 q2_1 q2_2 q2_3 q2_4]
[q3_0 q3_1 q3_2 q3_3 q3_4]
[q4_0 q4_1 q4_2 q4_3 q4_4]]
offset = 11.5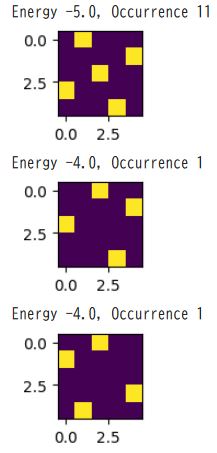
<この問題のポイント>
パズルのルールは多少は解釈(=言い換え)してもOK。2次元配列状の量子ビットを扱い、表示できるかも問われている。制約条件のみのため、明確に「コスト」を設定していた場合は再提出となる。
もっとも多かった間違いは、「星の8近傍に他の星があってはならない」を「どこの3×3をとっても星が1個」としてしまうこと。