21-28. 量子アニーリング（QUBO）で線形回帰（最小二乗法）

量子コンピュータ

2023/06/03

やること
QUBO式のおさらい
どうやって線形回帰（最小二乗法）するか？
コードと結果
さいごに

やること

以前、ポケモンを100匹ずつ捕まえて「高さ」と「重さ」の関係を調べました。図らずも、ビリリダマは大きくなるほど密度が下がるという不都合な真実を明らかにしてしまったわけですが。

それは置いておいて、今回はそのビリリダマのデータを用いて、QUBOで最小二乗法を行い回帰直線を求めてみたいと思います。

QUBO式のおさらい

QUBOで設定できる条件式については過去のまとめ記事をご参照ください↓

また、こちらでは量子ビットを8個（8bit）用いて0～255の整数を表しました。これも予習してください。

どうやって線形回帰（最小二乗法）するか？

ビリリダマ10匹のデータです。

height(m)	weight(kg)
0.31	5.75
0.4	8.56
0.47	8.42
0.4	7.78
0.54	10.25
0.36	6.79
0.56	11.51
0.43	7.66
0.32	6.99
0.6	10.61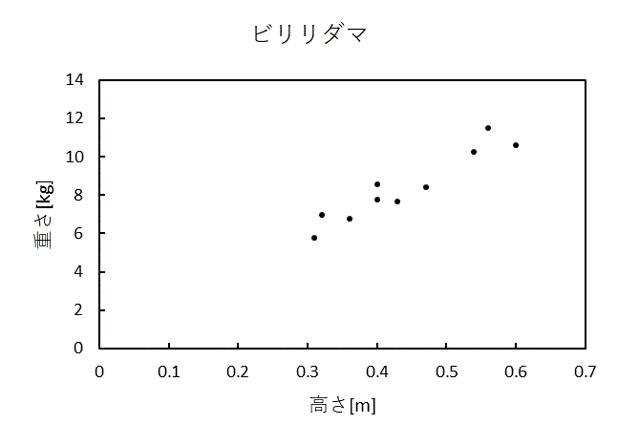

高さx、重さyとして「y=ax+b」の傾きaと切片bを求めます。とりあえずExcelで回帰直線を求めたのがこちらです。

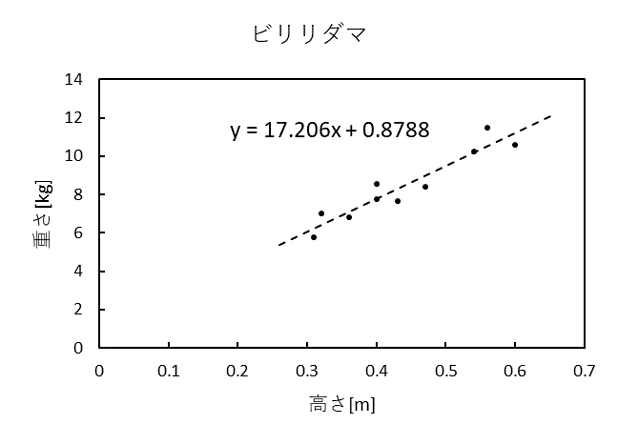
最小二乗法では「誤差の二乗の合計」ができるだけ小さくなるような傾きaと切片bを求めます。そこで、量子アニーリングではこの「誤差の二乗の合計」をエネルギーのペナルティに設定してやれば、最小エネルギーの解を求めることがそのまま最小二乗法に相当します。

例えば x=0.31 に着目すると、実データは 5.75 で、近似直線上の値は (a×0.31 + b) です。誤差は (5.75 – (a×0.31 + b)) で、これの二乗をペナルティにします。

ここで、aとbは量子ビットをそのまま割り当ててしまうと０と１しか取り得ません。そこで量子ビットを8bit使って0～255までの256段階の数を表す方法を活用します。この256段階を10～20に規格化することで「10～20の間の256段階の数値」を表すことができます。aは10～20の間だろうと見積もってこのように表現しましょう（10≦a＜20）。

#a0～a7は量子ビット（10≦a＜20）
a = 10 + 10 * ((128*a0 + 64*a1 + 32*a2 + 16*a3 + 8*a4 + 4*a5 + 2*a6 + a7) / 256)

同様に、0～1に規格化することで「0～1の間の256段階の数値」を表すことができます。bは0～1の間だろうと見積もってこのようにします（0≦b＜1）。

#b0～b7は量子ビット（0≦b＜1）
b = 0 + 1 * ((128*b0 + 64*b1 + 32*b2 + 16*b3 + 8*b4 + 4*b5 + 2*b6 + b7) / 256)

誤差の二乗はこのような式です。

H += (5.75 - (a*0.31 + b))**2

このaとbはそれぞれ8個の量子ビットの集合体で、展開した式はかなり長くなります。「え！こんな式立てて大丈夫なの？」と心配になりますが大丈夫です。QUBOでは２個の量子ビットの掛け算まで設定可能で、３個以上の量子ビットの掛け算はあってはいけません。冷静に展開してみると、３個以上の掛け算は現れないので大丈夫なのです。（なんか都合良すぎるような気もしますが）

コードと結果

from pyqubo import Binary
from dwave_qbsolv import QBSolv

#量子ビットを用意する
a0 = Binary('a0')
a1 = Binary('a1')
a2 = Binary('a2')
a3 = Binary('a3')
a4 = Binary('a4')
a5 = Binary('a5')
a6 = Binary('a6')
a7 = Binary('a7')

b0 = Binary('b0')
b1 = Binary('b1')
b2 = Binary('b2')
b3 = Binary('b3')
b4 = Binary('b4')
b5 = Binary('b5')
b6 = Binary('b6')
b7 = Binary('b7')

#aを2進数（8bit）で表す、10～20で規格化
a = 10 + 10 * ((128*a0 + 64*a1 + 32*a2 + 16*a3 + 8*a4 + 4*a5 + 2*a6 + a7) / 256)

#bを2進数（8bit）で表す、0～1で規格化
b = 0 + 1 * ((128*b0 + 64*b1 + 32*b2 + 16*b3 + 8*b4 + 4*b5 + 2*b6 + b7) / 256)

#データ1の誤差二乗ペナルティ
H = 0
H += (5.75 - (a*0.31 + b))**2

#データ2の誤差二乗ペナルティ
H += (8.56 - (a*0.4 + b))**2

#以降同様
H += (8.42 - (a*0.47 + b))**2
H += (7.78 - (a*0.4 + b))**2
H += (10.25 - (a*0.54 + b))**2
H += (6.79 - (a*0.36 + b))**2
H += (11.51 - (a*0.56 + b))**2
H += (7.66 - (a*0.43 + b))**2
H += (6.99 - (a*0.32 + b))**2
H += (10.61 - (a*0.6 + b))**2


#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()

#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=1000)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')

    #2進数から戻して確認
    a0,a1,a2,a3,a4,a5,a6,a7 = list(sample.values())[:8]
    b0,b1,b2,b3,b4,b5,b6,b7 = list(sample.values())[8:]
    print(f'a = {10 + 10 * ((128*a0 + 64*a1 + 32*a2 + 16*a3 + 8*a4 + 4*a5 + 2*a6 + a7) / 256)}')
    print(f'b = {0 + 1 * ((128*b0 + 64*b1 + 32*b2 + 16*b3 + 8*b4 + 4*b5 + 2*b6 + b7) / 256)}')

response
Sample:[1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1] Energy:-168.1485632324219 Occurrence:36
a = 17.1875
b = 0.88671875
Sample:[1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1] Energy:-168.14852859497074 Occurrence:20
a = 17.2265625
b = 0.87109375
Sample:[1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0] Energy:-168.14840820312506 Occurrence:3
a = 17.1875
b = 0.890625

最良の解は (a, b) = (17.188, 0.887) となりました。Excelで求めた傾きと切片は (17.206, 0.879) だったのでかなり近い値が得られたことになります。

aとbはそれぞれ8bitで表現したため256段階の飛び飛びの値しか取り得ません。したがって厳密な最適パラメータは求まりません。より厳密に近いパラメータを求めたければ、aは17～18の範囲に絞って、bは0.8～0.9の範囲に絞ってさらにアニーリングを繰り返すと良いでしょう。あるいは、9bitで表現すれば512段階で刻めるのでそういうアプローチでも良いでしょう。