やること
第2回ビネクラ杯の問題は、野口英世の画像を20×20個のパーツに分解し、並べ替えたり回転させたりして北里柴三郎を作るというものです。
ちょっと寄り道して、D-waveマシン(量子アニーリング)を使って挑戦してみましょう。今回はちょっと頭を使うので気合を入れます。
参考文献
D-waveのサービス「Leap」の導入はこちらを参考に。
D-Waveの新しいサービス、Leap2の使い方についてはこちら。

D-Waveの基本的な条件設定はこちら。
問題の基本的な解き方はこちら。
実行環境
WinPython3.6をおすすめしています。

Google Colaboratoryが利用可能です。


LeapからLeap2へ
しばらくLeapを触っていなかったせいか、昔のコードを実行するとエラーが出ました。
SolverFailureError: Problem not accepted because user *** has no remaining quota in project DEV月1分の実行時間が100%残っているのに期限切れとなっています。

これはLeapがLeap2へ移行したため、古いTrial Planが無効になったためです。Free Developer Accessというプランに変更することで解消されました。(Github連携が必要です)
pip, import
参考文献2を参考にD-waveのパッケージを最新版にします。
pip install -U dwave-ocean-sdk --user必要なパッケージをインポートします。
import cv2
import numpy as np
import matplotlib.pyplot as plt
from pyqubo import Binary
from dwave.system.composites import EmbeddingComposite
from dwave.system.samplers import DWaveSampler
from dwave_qbsolv import QBSolv画像の読み込みからパーツ分割まで
参考文献4とほとんど同じです。
#============================
# パラメータ
#============================
#画像
noguchi_file = 'vccup2_img1.png'
kitazato_file = 'vccup2_img2.png'
#たてよこ分割数
num = 2 #2, 4, 8, 10, 20など200の約数を指定可能
#1ブロックの幅
w = 200 // num
#============================
# 関数
#============================
#ndarray形式の画像を表示
def show(img):
plt.figure(figsize=(8, 8))
plt.imshow(img, vmin = 0, vmax = 255)
plt.gray()
plt.show()
plt.close()
print()
#ndarray形式のパーツを90°回転(反時計回りにn回)
def rotate(img, n):
return np.rot90(img, n)
#パーツセットから1枚の画像を再構成
def marge(ims):
tmp = [cv2.hconcat([ims[i*num + j] for j in range(num)]) for i in range(num)] #横長の短冊にして
img = cv2.vconcat([tmp[i] for i in range(num)]) #縦に並べる
return img
#============================
# 画像の読み込み
#============================
#野口英世をグレースケール(1ch)で読み込む(cv2で読むとndarrayになっている)
noguchi_img = cv2.imread(noguchi_file, cv2.IMREAD_GRAYSCALE)
#サイズの確認
print('noguchi_img.shape:{}'.format(noguchi_img.shape))
#表示
show(noguchi_img)
#北里柴三郎も読み込む
kitazato_img = cv2.imread(kitazato_file, cv2.IMREAD_GRAYSCALE)
print('kitazato_img.shape:{}'.format(kitazato_img.shape))
#表示
show(kitazato_img)
#============================
# 画像をパーツに分解する
#============================
#野口
noguchi_ims = []
for tanzaku in np.vsplit(noguchi_img, num): #横長の短冊にして
noguchi_ims += np.hsplit(tanzaku, num) #正方形に切る
noguchi_ims = np.array(noguchi_ims)
print('noguchi_ims.shape:{}'.format(noguchi_ims.shape))
#北里
kitazato_ims = []
for tanzaku in np.vsplit(kitazato_img, num): #横長の短冊にして
kitazato_ims += np.hsplit(tanzaku, num) #正方形に切る
kitazato_ims = np.array(kitazato_ims)
print('kitazato_ims.shape:{}'.format(kitazato_ims.shape))noguchi_img.shape:(200, 200)
kitazato_img.shape:(200, 200)



noguchi_ims.shape:(4, 100, 100)
kitazato_ims.shape:(4, 100, 100)考え方
量子アニーリングでどうやって最適化するか、考えていきます。実際の問題は20×20個のパーツに分割しますが、ここでは簡単のために2×2に分割するとし、回転なしとします。
量子ビットの置き方
まず、野口パーツと北里ブロックは次のように番号を振ります。(プログラムに合わせて0始まりにしています)
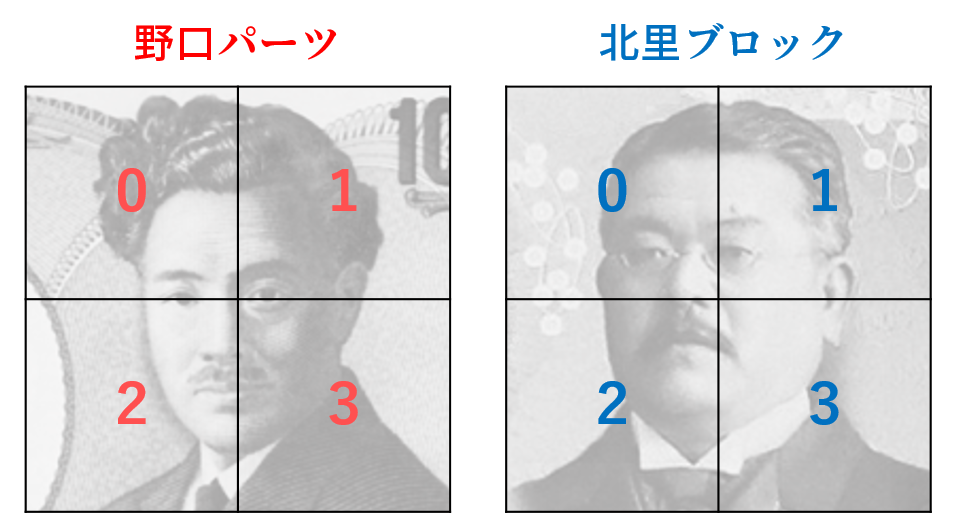

(パーツ数×ブロック数)個の量子ビットを用意し、次のように2次元配列に配置して考えます。想定される最適化結果は右側のように、どの行と列を見ても一つだけ「1」の状態です。
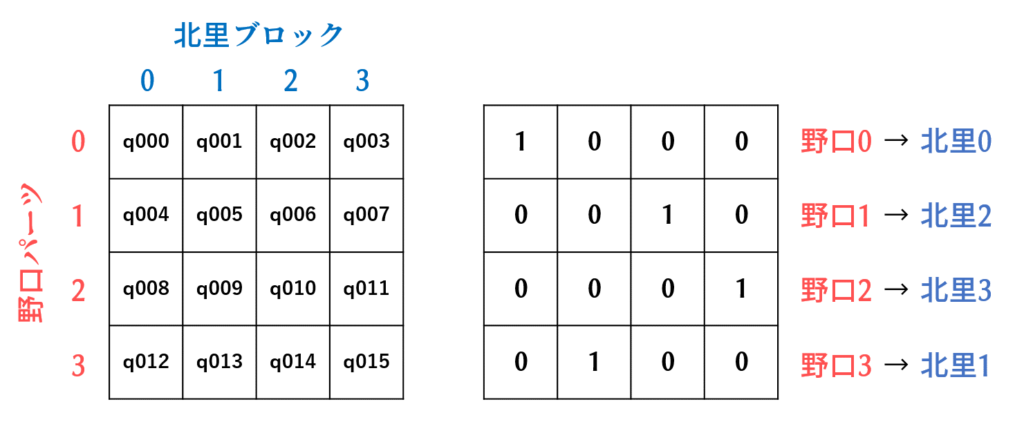

よって次のような画像ができあがります。赤字はパーツ番号です。


どの行と列を見ても一つだけ「1」の状態にするための設定
これまでにやったことがある設定です(参考文献3)。「n個の量子ビットからm個を1にする」の設定を各行と各列に行います。
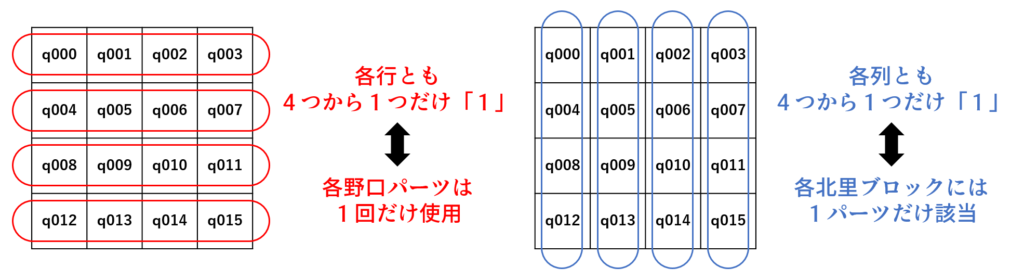

ただしこの設定だけでは、「パーツの重複はないが滅茶苦茶な並び」になってしまいます。
北里柴三郎に近くするための設定
ここで初めての設定を行います。各ブロックと各パーツの距離を計算します。4×4=16個の距離は各量子ビットに対応します。距離が近いところの量子ビットほど1になりやすいように設定します。
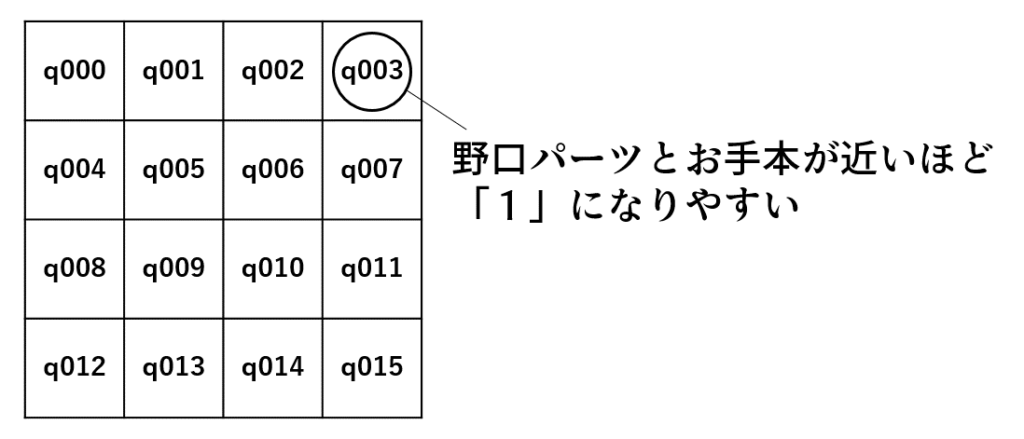

コードをどう書くか、うーんと考えて次のようにしました。
#条件を記述する
H = (q0 - 1 + k)**2kは「1へのなりにくさ(0.0~1.0)」です。「0へのなりやすさ」と考えても良いです。
Hはエネルギーを表しており、低いほど安定(=良い解)です。k=0.0の場合、q0=1においてHは最小になります(=q0は1になりやすい)。k=1.0の場合、q0=0においてHは最小になります(=q0は0になりやすい)。
組み合わせ最適化問題なので「こちらを立てればあちらが立たず」なのですが、ガチャガチャアニーリングしながら一番エネルギーが低くなる状態を見つけてくれることを祈ります。
コード
どの行と列を見ても一つだけ「1」の状態にするための設定
ここはサクッと。
#============================
# どの行と列を見ても一つだけ「1」の状態にするための設定
#============================
#量子ビットを用意する
for i in range(num**2**2):
command = 'q{:03} = Binary(\'q{:03}\')'.format(i, i)
print(command)
exec(command)
#条件を記述する関数(n個の量子ビットからm個だけ1にする)
def H_add(qbits, num):
command = '(' + ' + '.join(['q{:03}'.format(i) for i in qbits]) + ' - {})**2'.format(num)
print(command)
return eval(command)
#条件を記述していく
H = 0
#ブロックについてのfor
for i in range(num**2):
#あるブロックには野口パーツから一つしか採用されない
qbits = [i*(num**2) + j for j in range(num**2)]
H += H_add(qbits, 1)
#野口パーツについてのfor
for i in range(num**2):
#ある野口パーツは一つのブロックでしか採用されない
qbits = [i + j*(num**2) for j in range(num**2)]
H += H_add(qbits, 1)q000 = Binary('q000')
q001 = Binary('q001')
q002 = Binary('q002')
q003 = Binary('q003')
q004 = Binary('q004')
q005 = Binary('q005')
q006 = Binary('q006')
q007 = Binary('q007')
q008 = Binary('q008')
q009 = Binary('q009')
q010 = Binary('q010')
q011 = Binary('q011')
q012 = Binary('q012')
q013 = Binary('q013')
q014 = Binary('q014')
q015 = Binary('q015')
(q000 + q001 + q002 + q003 - 1)**2
(q004 + q005 + q006 + q007 - 1)**2
(q008 + q009 + q010 + q011 - 1)**2
(q012 + q013 + q014 + q015 - 1)**2
(q000 + q004 + q008 + q012 - 1)**2
(q001 + q005 + q009 + q013 - 1)**2
(q002 + q006 + q010 + q014 - 1)**2
(q003 + q007 + q011 + q015 - 1)**2量子ビットの定義と、4行および4列の設定ができています。
北里柴三郎に近くするための設定
先の条件設定を一般化した関数を作りました。次のように使います。
#条件を記述する関数2(n番目の量子ビットを1にしにくくする)
def H_add2(qbit, num):
command = '(q{:03} - 1 + {})**2'.format(qbit, num)
print(command)
return eval(command)
H += H_add2(量子ビット番号, 1へのなりにくさ)各ブロックと各パーツの距離を計算し、0~1に規格化します。距離が小さい部分ほど1になりやすくしたいので、「1へのなりにくさ」に距離を符号を変えずに渡してやります。また、ここでは最適化の確認のために野口パーツを並び替えて野口英世を作ってみます(途中のコメントアウトした部分で切り替えられます)。元の野口英世が完成すれば、最適化がうまくいったということです。
#============================
# 北里柴三郎に近くするための設定
#============================
#条件を記述する関数2(n番目の量子ビットを1にしにくくする)
def H_add2(qbit, num):
command = '(q{:03} - 1 + {})**2'.format(qbit, num)
print(command)
return eval(command)
#距離計算、ブロックと野口パーツの組み合わせで調べる
scores = []
for i in range(num**2):
for j in range(num**2):
#ブロック[i]に対する野口パーツ[j]の距離を計算
score = np.mean((noguchi_ims[i] - noguchi_ims[j])**2) #np.mean((kitazato_ims[i] - noguchi_ims[j])**2)
scores.append(score**2)
#scoresが0-1になるよう規格化
scores /= np.max(scores)
print(np.min(scores))
print(np.max(scores))
#スコアに応じて重みを調整
for i in range(num**2**2):
#スコアは距離なので、小さいほど結果を1にしやすくしたい
H += H_add2(i, 1.0*scores[i])0.0
1.0
(q000 - 1 + 0.0)**2
(q001 - 1 + 0.7789718996191202)**2
(q002 - 1 + 1.0)**2
(q003 - 1 + 0.906375006095451)**2
(q004 - 1 + 0.7789718996191202)**2
(q005 - 1 + 0.0)**2
(q006 - 1 + 0.9200691213030905)**2
(q007 - 1 + 0.8568285123655662)**2
(q008 - 1 + 1.0)**2
(q009 - 1 + 0.9200691213030905)**2
(q010 - 1 + 0.0)**2
(q011 - 1 + 0.8253950632806928)**2
(q012 - 1 + 0.906375006095451)**2
(q013 - 1 + 0.8568285123655662)**2
(q014 - 1 + 0.8253950632806928)**2
(q015 - 1 + 0.0)**2使うパーツは野口、お手本も野口ですから、2次元配列状に配置した量子ビットたちの対角成分(0, 5, 10, 15番)の「1へのなりにくさ」は0.0が入っていて、これらのビットが1になる解が最適解です。
D-waveでサンプリング
quboという謎のマトリックスにしてD-waveマシンでサンプリングします。あまり計算が長くなるともったいないのでtimeout=5.0を指定しました。
#============================
# D-waveでサンプリング
#============================
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print('qubo\n{}'.format(qubo))
#D-waveの設定
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://cloud.dwavesys.com/sapi/',
token='your_token',
solver='DW_2000Q_6'))
#問題を分割してサンプリングしまくる
response = QBSolv().sample_qubo(qubo, solver=sampler, num_repeats=1000, timeout=5.0)
#レスポンスの確認
count = 0
print('response')
for (sample, energy, occurrences) in response.data():
print('Sample:{} Energy:{} Occurrences:{}'.format(list(sample.values()), energy, occurrences))
#1番目を保存しておく
if count == 0:
best_sample = np.array(list(sample.values()))
count += 1
if count > 20:
break
#最頻解の確認
print('best_sample\n{}'.format(best_sample))qubo
{('q000', 'q001'): 2.0, ('q000', 'q002'): 2.0, ('q000', 'q003'): 2.0, ('q000', 'q004'): 2.0, ('q000', 'q008'): 2.0, ('q000', 'q012'): 2.0, ('q001', 'q002'): 2.0, ('q001', 'q003'): 2.0, ('q001', 'q005'): 2.0, ('q001', 'q009'): 2.0, ('q001', 'q013'): 2.0, ('q002', 'q003'): 2.0, ('q002', 'q006'): 2.0, ('q002', 'q010'): 2.0, ('q002', 'q014'): 2.0, ('q003', 'q007'): 2.0, ('q003', 'q011'): 2.0, ('q003', 'q015'): 2.0, ('q004', 'q005'): 2.0, ('q004', 'q006'): 2.0, ('q004', 'q007'): 2.0, ('q004', 'q008'): 2.0, ('q004', 'q012'): 2.0, ('q008', 'q009'): 2.0, ('q008', 'q010'): 2.0, ('q008', 'q011'): 2.0, ('q008', 'q012'): 2.0, ('q012', 'q013'): 2.0, ('q012', 'q014'): 2.0, ('q012', 'q015'): 2.0, ('q005', 'q006'): 2.0, ('q005', 'q007'): 2.0, ('q005', 'q009'): 2.0, ('q005', 'q013'): 2.0, ('q009', 'q010'): 2.0, ('q009', 'q011'): 2.0, ('q009', 'q013'): 2.0, ('q013', 'q014'): 2.0, ('q013', 'q015'): 2.0, ('q006', 'q007'): 2.0, ('q006', 'q010'): 2.0, ('q006', 'q014'): 2.0, ('q010', 'q011'): 2.0, ('q010', 'q014'): 2.0, ('q014', 'q015'): 2.0, ('q007', 'q011'): 2.0, ('q007', 'q015'): 2.0, ('q011', 'q015'): 2.0, ('q000', 'q000'): -3.0, ('q001', 'q001'): -1.4420562007617597, ('q002', 'q002'): -1.0, ('q003', 'q003'): -1.187249987809098, ('q004', 'q004'): -1.4420562007617597, ('q008', 'q008'): -1.0, ('q012', 'q012'): -1.187249987809098, ('q005', 'q005'): -3.0, ('q009', 'q009'): -1.159861757393819, ('q013', 'q013'): -1.2863429752688675, ('q006', 'q006'): -1.159861757393819, ('q010', 'q010'): -3.0, ('q014', 'q014'): -1.3492098734386144, ('q007', 'q007'): -1.2863429752688675, ('q011', 'q011'): -1.3492098734386144, ('q015', 'q015'): -3.0}
response
Sample:[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1] Energy:-12.0 Occurrences:1001
best_sample
[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]解から画像を再構成して確認
#============================
# 野口パーツを当てはめる
#============================
#新しいパーツ配列を用意
new_ims = np.zeros(kitazato_ims.shape, int)
#ブロックについてのfor
for i in range(num**2):
#あるブロックに対応する量子ビット
candidate = best_sample[i*(num**2) : (i+1)*(num**2)]
#採用された野口パーツ
new_ims[i] = noguchi_ims[np.argmax(candidate)]
#画像を再構成して表示
new_img = marge(new_ims)
show(new_img)

狙い通り、野口英世ができました。分かりやすいように白線を入れてあります。
よし、分割数を2×2から増やしながら「野口が完成するか(コントロール)」と「北里の作成(本番)」を試してみます。


4×4野口は再現性がありましたが、4×4北里は再現性なしでした。
N×Nに分割するとき、この手法で必要な量子ビット数は(N^2)^2なので、8×8だと4096ビット。問題を分割していい感じにやってくれるとはいえ難しいです。
ハイブリッドソルバー「 hybrid_v1 」
Leap2ではハイブリッドソルバー「 hybrid_v1 」が追加されているようです。コンソールで確認すると、月に約18分与えられるようです。参考文献2に従って該当部分を書き換えます。
import cv2
import numpy as np
import matplotlib.pyplot as plt
from pyqubo import Binary
import dimod
from dwave.system import LeapHybridSampler#============================
# D-waveでサンプリング
#============================
#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
bqm = dimod.BQM.from_numpy_matrix(qubo)
#設定とサンプリング
response = LeapHybridSampler(token='your_token').sample(bqm)

はい。結果は同様でした。
野口4×4の解で「Occurrences:1」なので発見はギリギリな感じがします。もっと100万回くらいサンプリングしないといけない気がしますが、どうなんでしょうか。
結論
ということで、令和最新版の量子現代アート「D-waveで野口英世を並び替えて作った北里柴三郎」をご査収ください。