やること
前回は画像のフーリエ変換の基本を学びました。
この手法では画像が持つ周波数成分が可視化できます。つまり、細かな模様なのか粗い模様なのかが解析できるということです。今回はこれを応用して布のしわをフーリエ変換で解析してみます。
用いた画像
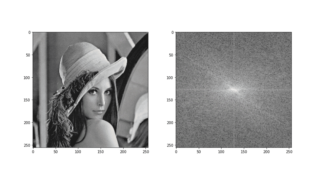
こちらの写真の左側から画像①(しわ無し)、右側から画像②(しわ小)をトリミングしました。
こちらの写真の右側から画像③(しわ大)をトリミングしました。
画像①(しわ無し)
画像②(しわ小)
画像③(しわ大)
明るさが若干異なるので、グレースケール輝度値の中央値が同じになるように補正して用います。
フーリエ変換の結果
画像①(しわ無し)
元画像(輝度値補正済み)

FFT画像

画像②(しわ小)
元画像(輝度値補正済み)

FFT画像

画像③(しわ大)
元画像(輝度値補正済み)

FFT画像
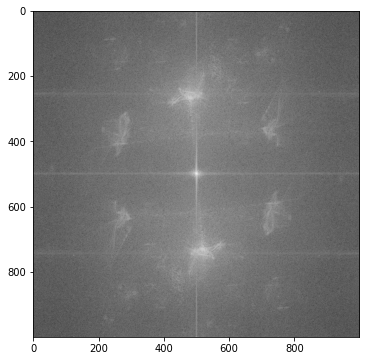
考察
「キ」のような特徴が見えました。この特徴はしわが大きいほど滲んでぼやけるようです。ここではしわの規模によるFFT画像の特徴を調べたいので、生地の地の目に由来している特徴は無視したいです。そこで画像②と画像③のFFT画像からそれぞれ画像①のFFT画像を減算してみました。
画像②FFT-画像①FFT

画像③FFT-画像①FFT
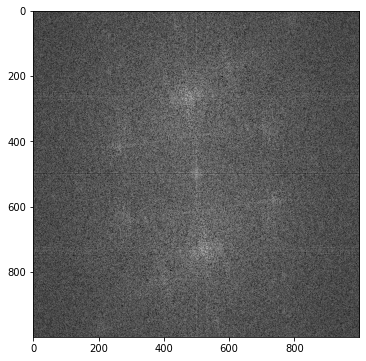
何とも言えない感じです。もう少し地の目を分離する工夫を考えてみましょう。
シフトと回転による周波数成分の変化
ここで、ランダムにシフト(上下左右にずらす)させながらトリミングした画像群と、0~99°まで回転させながらトリミングした画像群を用意して、それぞれフーリエ変換してみました。地の目には一定の方向があることから、シフトで変化せず回転で変化する特徴は地の目由来である、と考えて良いのではないでしょうか。

画像①(しわ無し)
ランダムシフト

回転

画像②(しわ小)
ランダムシフト
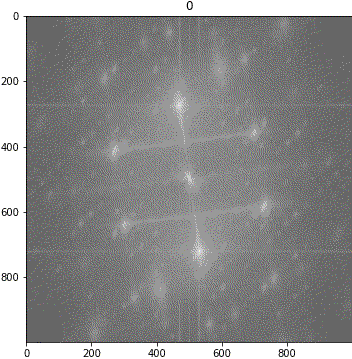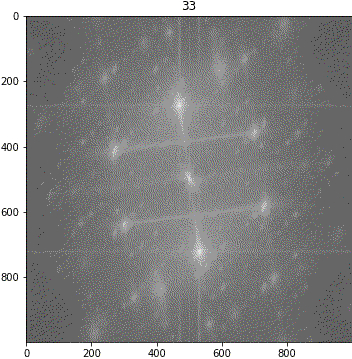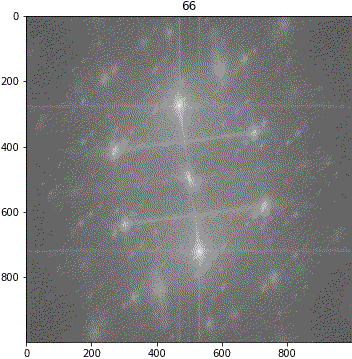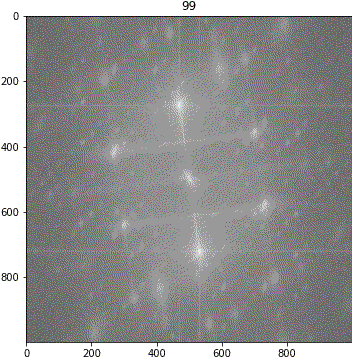
回転
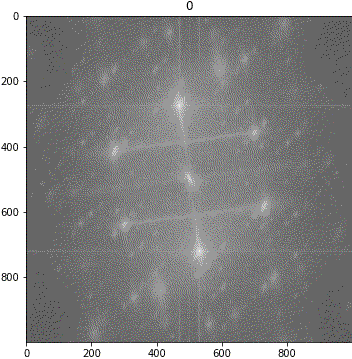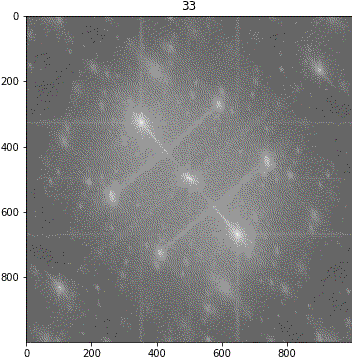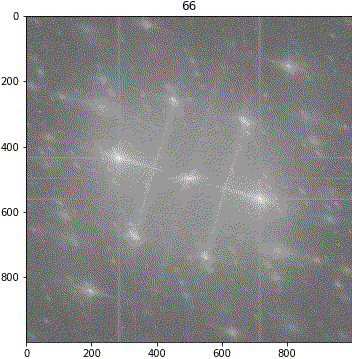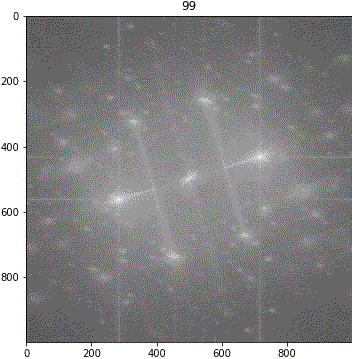
画像③(しわ大)
ランダムシフト
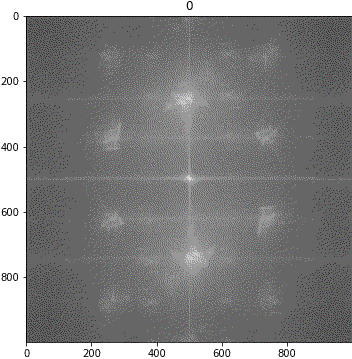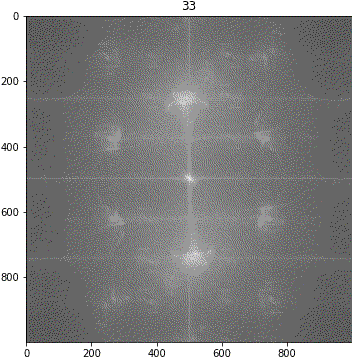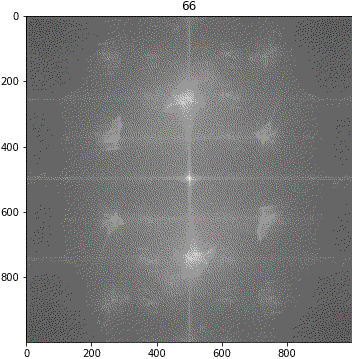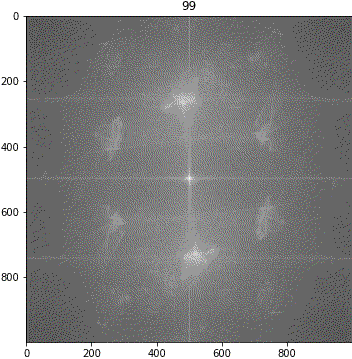
回転
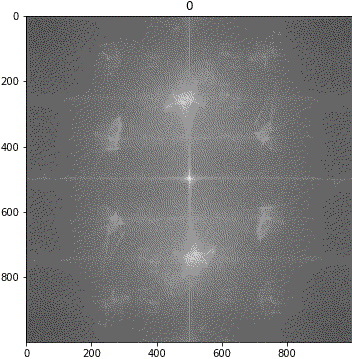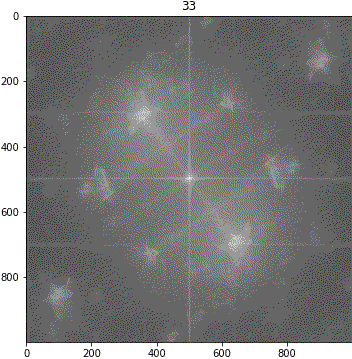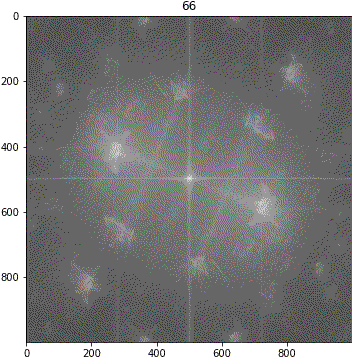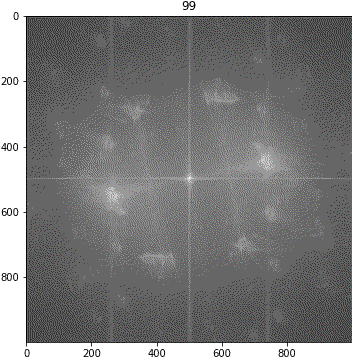
考察
解釈が難しいながらも、「キ」の特徴は地の目由来だろうということが示唆されました。しわについて、画像③に強い十字成分が出ていることに新たに気が付きました。しかも生地が回転しても十字成分は回転しません。要検証です。
まとめ
限られた検証でしたが、FFT画像について得られた知見をまとめます。
- 地の目によって特徴点や特徴線が現れる
- しわが大きいほど周辺(高周波成分)の特徴点と特徴線が滲む / ぼやける
- しわが大きいほど中心(低周波成分)が明るく鮮明に現れる
- しわが大きいほど十字成分が現れる(要検証)
まだ示唆のレベルなので、様々な布で検証して一般的な知見を得たいと思っています。また「滲み具合」や「明るさ」を定量的に比較する方法も考えなければいけません。このあたりは論文があるかもしれません。