5-11. レコメンドシステムではなぜユークリッド距離ではなくコサイン類似度が用いられるのか

[H] 小ネタ / 検証

2021/09/05

概要
ユークリッド距離とは
コサイン類似度とは
ユークリッド距離とコサイン類似度に差が出る場面
レコメンドシステムではなぜコサイン類似度が用いられる？
あとがき
参考文献

概要

２つのデータがどれくらい似ているかを知るには「距離」を調べます。ユークリッド距離はもっとも基本的な距離の一つです。一方でコサイン類似度というものもあり、レコメンドシステムや機械学習アルゴリズムにおいてデータ間の距離の指標に用いられることがあります。

今日は、レコメンドシステムではなぜユークリッド距離でなくコサイン類似度を使用することが多いかを考えてみます。

ユークリッド距離とは

ユークリッド距離は２点間の距離を算出する方法の一つで、２点が直線的にどれだけ離れているのかを示しています。

$d(A, B) = \sqrt{\sum^n_{i=1} (A_i - B_i)^2}$

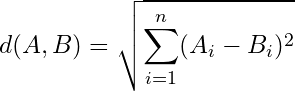
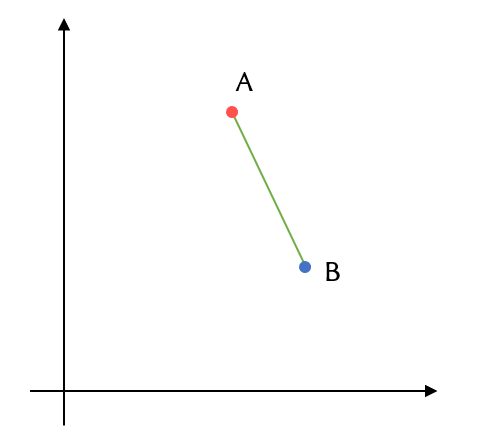
ユークリッド距離は値が小さいほど類似度が高いことを意味します。図は２次元ですが何次元でもOKです。

コサイン類似度とは

コサイン類似度は２点間の角度を算出します。

$c(A, B) = \frac{\sum^n_{i=1} A_i B_i}{\sqrt{\sum^n_{i=1} A^2_i} \sqrt{\sum^n_{i=1} B^2_i}}$

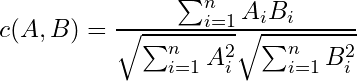
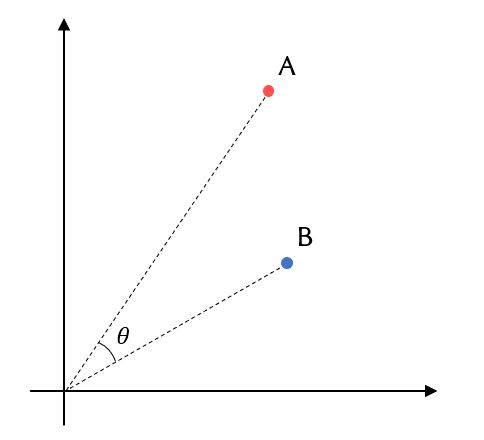
この式は cos(θ) そのものです。コサイン類似度は -1 から +1 の範囲をとり、+1 に近いほど類似度が高いことを意味します。こちらも図は２次元ですが何次元でもOKです。

なぜ “距離” ではなく “類似度” と呼ばれる？

コサイン類似度は -1 から +1 の範囲の値を取ります。マイナスの値を取ることもあり距離の公理を満たさないことから、”距離” ではなく “類似度” と呼ばれています。

注意点として、レコメンドシステムでユーザーの購入数や閲覧数を用いている場合、これらは０または正の値しか取り得ないため、コサイン類似度は０～１の範囲となります。数式的に言えば、θの値が 0 ≤ θ ≤ $\pi$ /2 であり、これに伴い cos(θ)の値が 0 ≤ cos(θ) ≤ 1 となるためです。

ユークリッド距離とコサイン類似度に差が出る場面

２点と原点が一直線上にある場合

この場合、コサイン類似度は１であり区別がつかないほど類似していることになりますが、ユークリッド距離はしっかりあります。

２点が原点を挟んですぐ隣り合わせにある場合

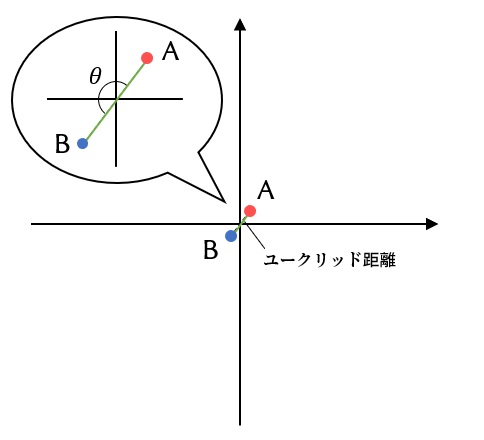
この場合、ユークリッド距離は非常に小さいですが、コサイン類似度は -1（角度180°）となります。

レコメンドシステムではなぜコサイン類似度が用いられる？

あるECサイトはPCパーツ、Tシャツの２つの商品カテゴリだけを扱っています。そして、ユーザーが何に関心があるかを各カテゴリの購入点数で表すことにしました。つまり、各ユーザーの特徴は２次元のベクトルで表されます。

ここで、３人のユーザーのベクトルは次とします。

ユーザー	PCパーツ	Tシャツ
A	45	24
B	12	5
C	5	12

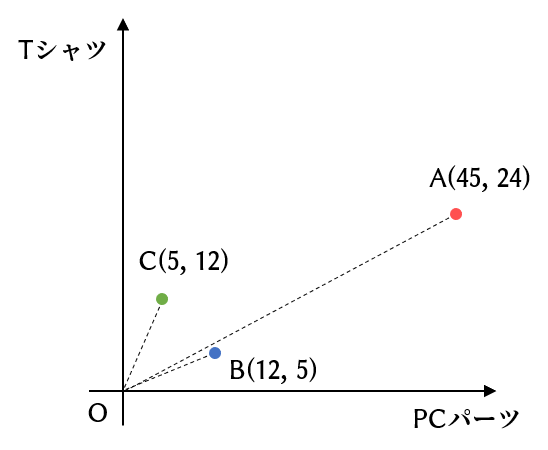
ユークリッド距離

３点間のユークリッド距離を求めてみます。

$AB = \sqrt{(45 - 12)^2 + (24 - 5)^2} \fallingdotseq 38.1$

$AC = \sqrt{(45 - 5)^2 + (24 - 12)^2} \fallingdotseq 41.8$

$BC = \sqrt{(12 - 5)^2 + (5 - 12)^2} \fallingdotseq 9.9$

コサイン類似度

コサイン類似度も求めてみます。

$cos(AOB) = \frac{45 \times 12 + 24 \times 5}{\sqrt{45^2 + 24^2} \sqrt{12^2 + 5^2}} \fallingdotseq 0.99$

$cos(AOC) = \frac{45 \times 5 + 24 \times 12}{\sqrt{45^2 + 24^2} \sqrt{5^2 + 12^2}} \fallingdotseq 0.77$

$cos(BOC) = \frac{12 \times 5 + 5 \times 12}{\sqrt{12^2 + 5^2} \sqrt{5^2 + 12^2}} \fallingdotseq 0.71$

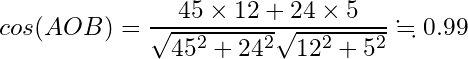
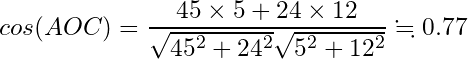
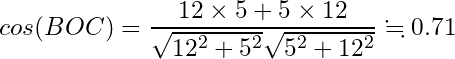
比較

さて、ユーザーAは「PCパーツに興味があるヘビーユーザー」、ユーザーBは「PCパーツに興味があるライトユーザー」、ユーザーCは「Tシャツに興味があるライトユーザー」と解釈できます。

ここでユーザーBにレコメンドする商品は何が良いでしょうか？

ユークリッド距離に基づけば、距離BCが比較的小さいですので、Cがよく買っているTシャツを勧めることになります。一方でコサイン類似度に基づけば、cos(AOB)が比較的大きいですから、Aがよく買っているPCパーツを勧めることになります。

大雑把に言えば、ユークリッド距離は要素の絶対値に強く影響され、ユーザーの利用頻度（ライトユーザーかヘビーユーザーか）で分ける傾向があります。一方、コサイン類似度は要素の絶対値を無視して商品のカテゴリで分ける傾向があります。ECサイトではカテゴリを重視したほうが良いレコメンドができるという考えからコサイン類似度が採用されやすいわけです。上の例ではBさんにPCパーツを勧めることになるでしょう。

コサイン類似度を採用するメリット

AさんがPCマニアで、よく高級キーボードを買っていたとします。BさんもPCには興味がありますが、そんなに高いキーボードは買ったことがありません。Bさんに高級キーボードをレコメンドすれば、興味が増してよりヘビーなユーザーに成長してくれるかもしれません。そうすればECサイトとしても儲かります。

コサイン類似度を採用するデメリット

Aさんが重度のPCマニアで、よくCPUグリスや水冷用クーラントを買っていたとします。このような商品をライトユーザーであるBさんに勧めるのはいかがでしょうか？それよりも無難にTシャツを勧めておいたほうが買ってくれる可能性が高いかもしれません。

あとがき

ただし、「ECサイトでは絶対にコサイン類似度」とは言い切れません。どんな距離の指標を採用するかは、何を重視するかによります。ユーザーの購入履歴ではなく閲覧履歴を使ったほうが良い場合もあるでしょう。また「車を買った人にまた車を勧める」なんてアルゴリズムはナンセンスですから、カー用品やキャンプ用品を勧めたほうが良いでしょう。レコメンドシステムは売上に直結しますから、適切なデータ解析に基づいた判断が必要になります。（cf. おむつとビール）