本記事の内容は2019年5月13日に更新されました。
やること
二重円環よりも三重円環の方が難しいと思います(乱心)。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
import
まずは、今回使うパッケージをインポートします。今回はmathも使います。
import math
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcopt関数の準備
巡回セールスマン問題の作成。ここで三重円環を作成します。town_numは3の倍数に設定する必要があります。
#巡回セールスマン問題の作成
def create_tsp(town_num):
#町のx座標とy座標の配列を作成
town_x, town_y = [], []
#三重円環状に配置
for i in range(0, 360, 360//(town_num//3)):
town_x.append(1.0 * math.sin(math.radians(i)))
town_y.append(1.0 * math.cos(math.radians(i)))
town_x.append(0.8 * math.sin(math.radians(i)))
town_y.append(0.8 * math.cos(math.radians(i)))
town_x.append(0.3 * math.sin(math.radians(i)))
town_y.append(0.3 * math.cos(math.radians(i)))
town_x = np.array(town_x)
town_y = np.array(town_y)
return town_x, town_y(必須)評価関数。これまでと同じです。
#巡回セールスマン問題の評価関数
def tsp_score(para):
#スコアの計算(今回は直接returnする)
return np.sum(((town_x[para][:-1] - town_x[para][1:])**2 + (town_y[para][:-1] - town_y[para][1:])**2)**0.5)(任意)ひとつのパラメータ群を可視化する関数。軸範囲は自動にします。
#paraの可視化
def tsp_show_para(para, **info):
#2-opt処理中の諸情報はinfoという辞書に格納されて渡されます
#これらを受け取って使用することができます
step_num = info['step_num']
score = info['score']
#プロット(および保存)
plt.figure(figsize=(6, 6))
plt.plot(town_x[para], town_y[para], 'ok-')
plt.xlabel('x'); plt.ylabel('y')
#plt.xlim([0, 1]); plt.ylim([0, 1])
plt.title('step={}, score={}'.format(step_num, score))
#plt.savefig('save/{}.png'.format(step_num))
plt.show()
print()(任意)すべてのパラメータ群を可視化する関数。これも軸範囲は自動にします。
#巡回セールスマン問題のpoolの可視化
def tsp_show_pool(pool, **info):
#GA中の諸情報はinfoという辞書に格納されて渡されます
#これらを受け取って使用することができます
gen = info['gen']
best_index = info['best_index']
best_score = info['best_score']
mean_score = info['mean_score']
mean_gap = info['mean_gap']
time = info['time']
#プロット(および保存)
plt.figure(figsize=(6, 6))
#poolを100個まで薄い黒でプロット
for para in pool[:100]:
plt.plot(town_x[para], town_y[para], 'ok-', alpha=(2.0/len(pool[:100])))
#エリートは赤でプロット
plt.plot(town_x[pool[best_index]], town_y[pool[best_index]], 'or-')
#タイトルをつけて表示
plt.xlabel('x'); plt.ylabel('y')
#plt.xlim([0, 1]); plt.ylim([0, 1])
plt.title('gen={}, best={} mean={} time={}'.format(gen, best_score, mean_score, time))
#plt.savefig('save/{}.png'.format(gen_num))
plt.show()
print()2-opt法で最適化
局所最適化と比較します。town_numは3の倍数にする必要があるので21にしました。乱数シードは固定せずに何度か実行してみます。
#巡回セールスマン問題の作成
town_num = 30
town_x, town_y = create_tsp(town_num)
#適当に道順を作成
para = np.arange(town_num)
nr.shuffle(para)
#2-opt法で最適化
para, score = vcopt().opt2(para, #para
tsp_score, #score_func
0.0, #aim
show_para_func=tsp_show_para, #show_para_func=None
seed=None) #seed=None
#結果の表示
print(para)
print(score)実行結果
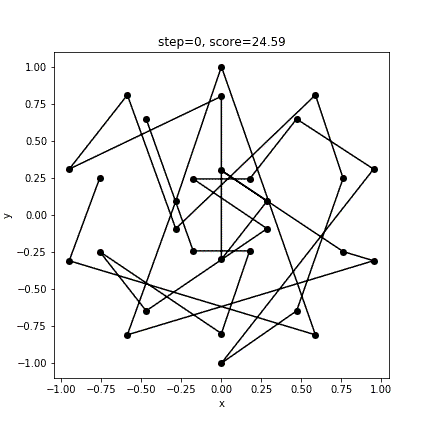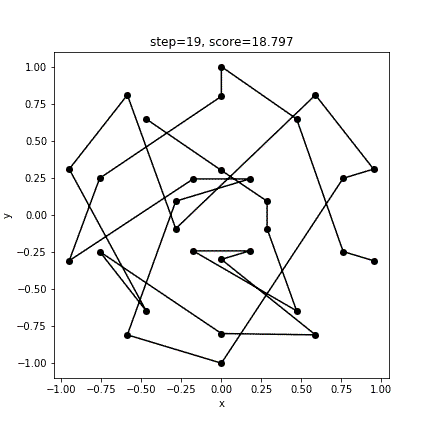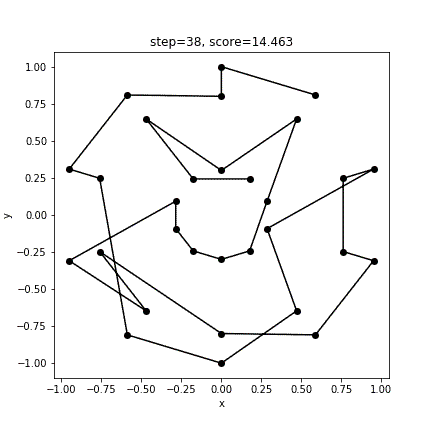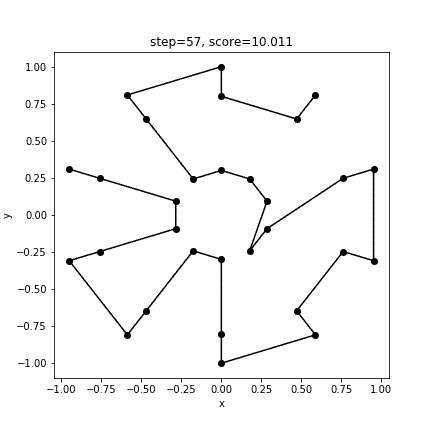
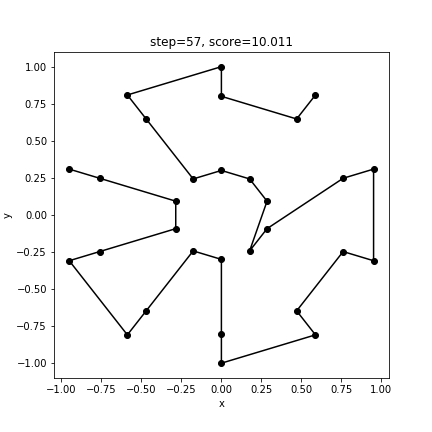
[ 3 4 1 0 27 28 29 2 5 8 14 11 7 6 9 10 13 12 15 16 17 20 19 18 21 22 23 26 25 24]
10.0106496929063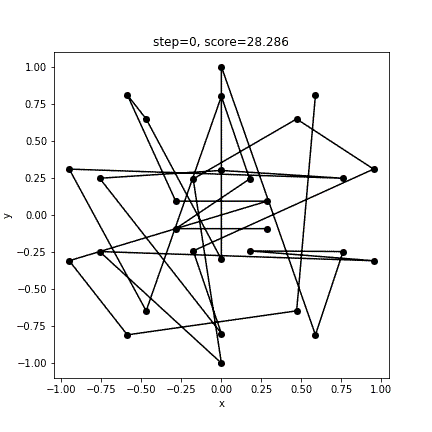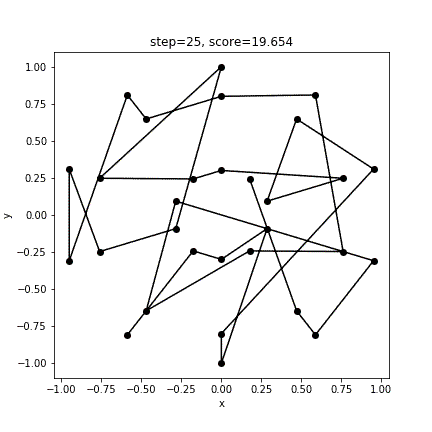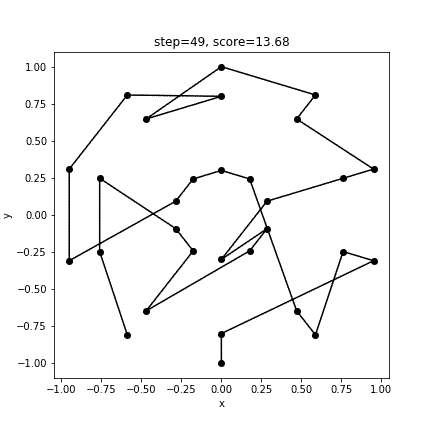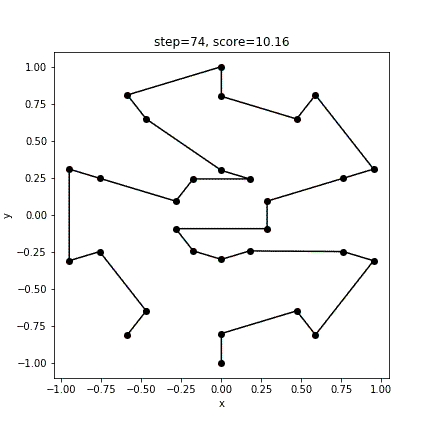
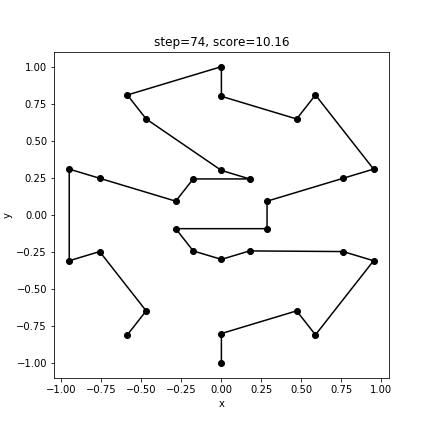
[18 19 22 21 24 25 26 29 5 2 28 27 0 1 4 3 6 7 8 11 23 20 17 14 10 9 12 13 16 15]
10.160237818464905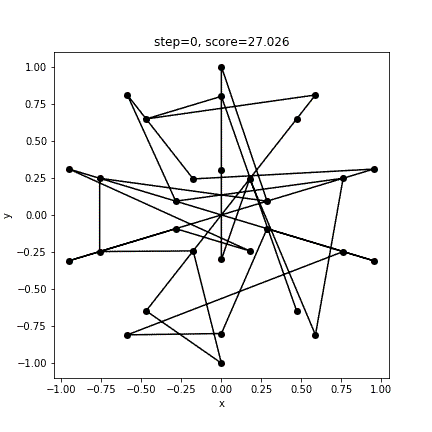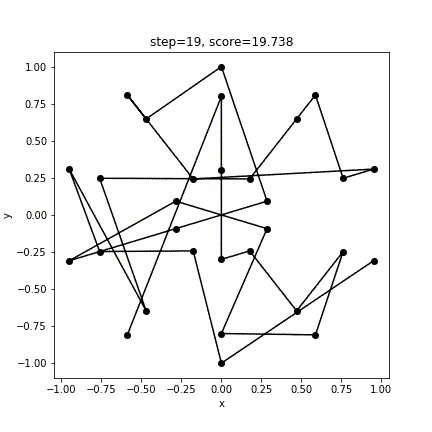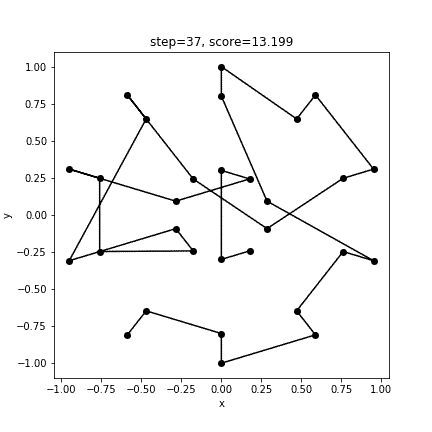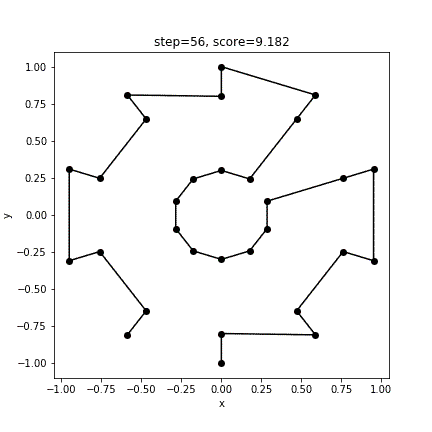
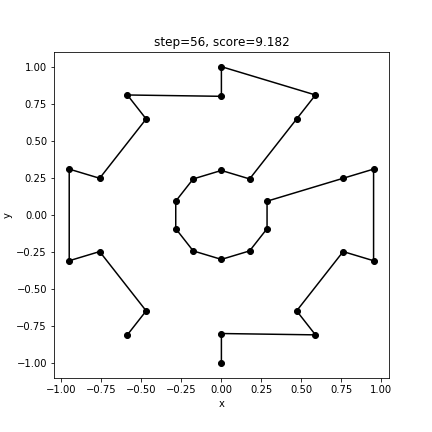
[18 19 22 21 24 25 28 27 1 0 3 4 5 2 29 26 23 20 17 14 11 8 7 6 9 10 13 12 16 15]
9.1817841316701383回目は非常に短い距離が出ました。GAはこれを超えられるのでしょうか。
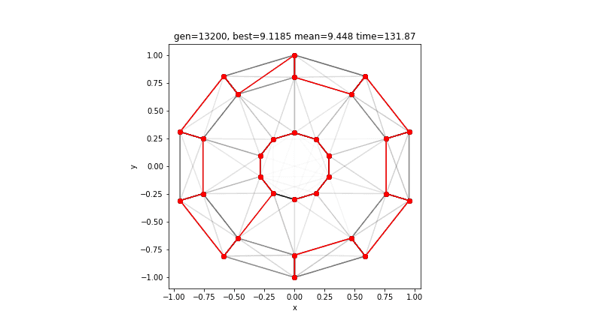
GAで最適化
こちらも問題を作成し、GAを実行します。
#巡回セールスマン問題の作成
town_num = 30
town_x, town_y = create_tsp(town_num)
#パラメータ範囲
para_range = np.arange(town_num)
#GAで最適化
para, score = vcopt().tspGA(para_range, #para_range
tsp_score, #score_func
0.0, #aim
show_pool_func=tsp_show_pool, #show_pool_func=None
seed=1) #seed=None
#結果の表示
print(para)
print(score)実行結果
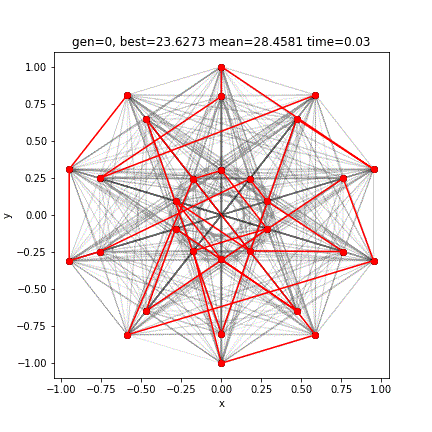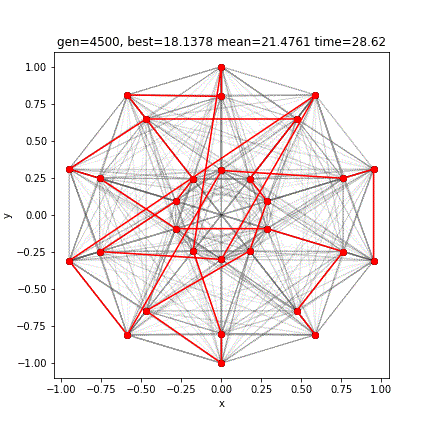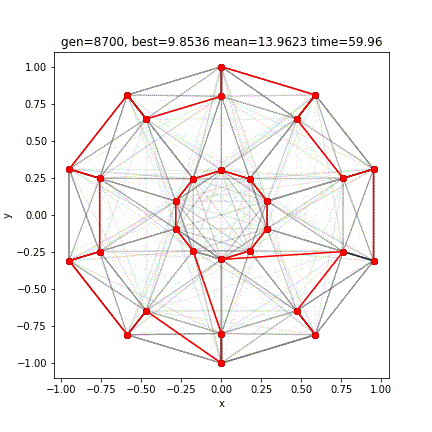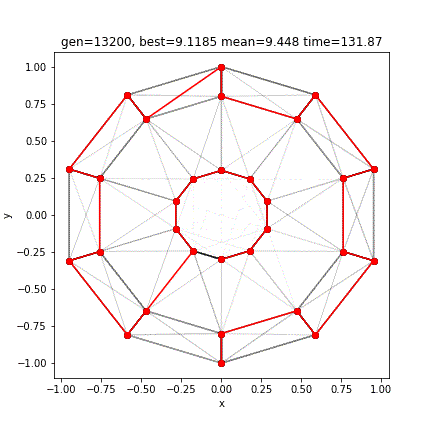

[12 13 10 9 6 7 4 3 0 1 28 27 24 25 22 21 18 19 20 23 26 29 2 5 8 11 14 17 16 15]
9.118536488623956GAの勝利です。外側で始まって内側で終わるという道を選んだようです。