本記事の内容は2019年5月13日に更新されました。
やること
ナップザック問題をGAで最適化してみます。
実行環境
WinPython3.6をおすすめしています。
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
import
まずは、今回使うパッケージをインポートします。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcopt問題設定
ナップザック問題として、「決められた金額をできるだけ少ない枚数の紙幣・硬貨で支払う」というコイン問題を考えます。今回購入したいものはこちら。
INTEL インテル CPU Corei9-9900K INTEL300シリーズChipsetマザーボード対応 BX80684I99900K【BOX】
2019/3/21時点で65,858円です(高い)。四捨五入して65,860円としましょう。
これを10000円札、5000円札、1000円札、500円玉、100円玉、50円玉、10円玉の7種類を組み合わせて支払いますが、できるだけ少ない枚数にするという問題です。各紙幣は0~9枚まで取ることができます。
最適解
冷静に考えれば最適解はわかります。いつもレジでやっていることです。(私は現金派)
[10000, 5000, 1000, 500, 100, 50, 10]円 → [6, 1, 0, 1, 3, 1, 1]枚(必須)評価関数
#ナップザック問題の評価関数
def money_score(para):
money = para[0]*10000 + para[1]*5000 + para[2]*1000 + para[3]*500 + para[4]*100 + para[5]*50 + para[6]*10
num = np.sum(para)
#スコアの計算(直接returnする)
return (abs(65860 - money) + 1) * num**2moneyは合計金額、numは合計枚数です。moneyは65860に近づけ、かつ、numは少なくするために、このような評価関数にしました。この評価関数が小さくなる方向に最適化します。
(任意)すべてのパラメータ群を可視化する関数
poolを受け取って、積み上げ棒グラフを並べます。
#ナップザック問題のpoolの可視化
def money_show_pool(pool, **info):
#GA中の諸情報はinfoという辞書に格納されて渡されます
#これらを受け取って使用することができます
gen = info['gen']
best_index = info['best_index']
best_score = info['best_score']
mean_score = info['mean_score']
mean_gap = info['mean_gap']
time = info['time']
#プロット(および保存)
plt.figure(figsize=(6, 6))
#poolを100個まで積み上げ棒グラフでプロット
x = np.arange(len(pool[:100]))
plt.bar(x, pool[:100, 0]*10000)
plt.bar(x, pool[:100, 1]*5000, bottom=pool[:, 0]*10000)
plt.bar(x, pool[:100, 2]*1000, bottom=pool[:, 0]*10000 + pool[:, 1]*5000)
plt.bar(x, pool[:100, 3]*500, bottom=pool[:, 0]*10000 + pool[:, 1]*5000 + pool[:, 2]*1000)
plt.bar(x, pool[:100, 4]*100, bottom=pool[:, 0]*10000 + pool[:, 1]*5000 + pool[:, 2]*1000 + pool[:, 3]*500)
plt.bar(x, pool[:100, 5]*50, bottom=pool[:, 0]*10000 + pool[:, 1]*5000 + pool[:, 2]*1000 + pool[:, 3]*500 + pool[:, 4]*100)
plt.bar(x, pool[:100, 6]*10, bottom=pool[:, 0]*10000 + pool[:, 1]*5000 + pool[:, 2]*1000 + pool[:, 3]*500 + pool[:, 4]*100 + pool[:, 5]*50)
#タイトルをつけて表示
plt.title('gen={}, best={} mean={} time={}'.format(gen, best_score, mean_score, time))
plt.ylim([0, 80000])
#plt.savefig('save/GA_{}.png'.format(gen_num))
plt.show()
print()GAで最適化
離散的なGAはvcopt().dcGA()で実行します。
#パラメータ範囲
para_range = [[i for i in range(10)] for j in range(7)]
#GAで最適化
para, score = vcopt().dcGA(para_range, #para_range
money_score, #score_func
0.0, #aim
show_pool_func=money_show_pool, #show_para_func=None
seed=None) #seed=None
#結果の表示
print(para)
print(score)実行結果
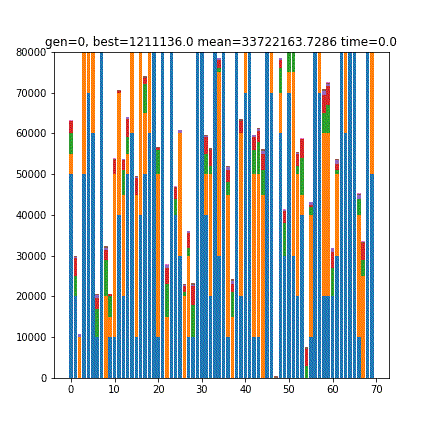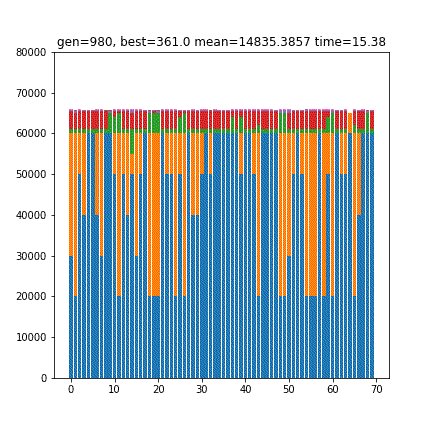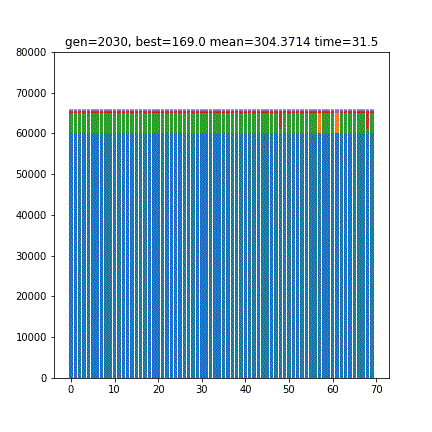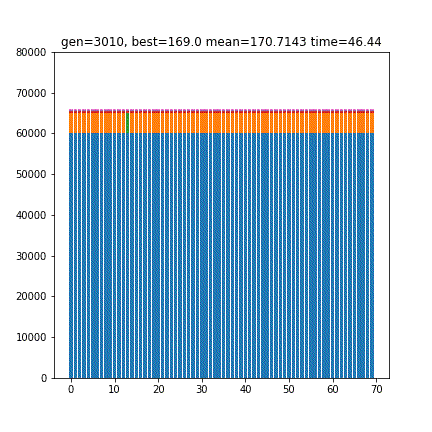
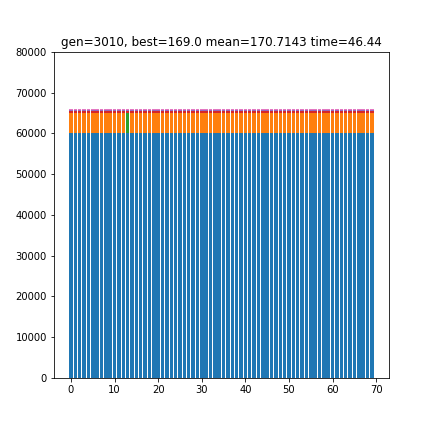
[6 1 0 1 3 1 1]
169.0青は10000円札、オレンジは5000円札、緑は1000円札、赤は500円玉…といった色付けになっています。合計金額が65860円付近に収束しているのがわかります。
結果、3010世代の進化により、各枚数が[6 1 0 1 3 1 1]であることと、最小スコア169が得られました。スコアは、
#スコアの計算
return (abs(65860 - money) + 1) * num**2からも分かる通り、合計枚数13の二乗に由来しています。