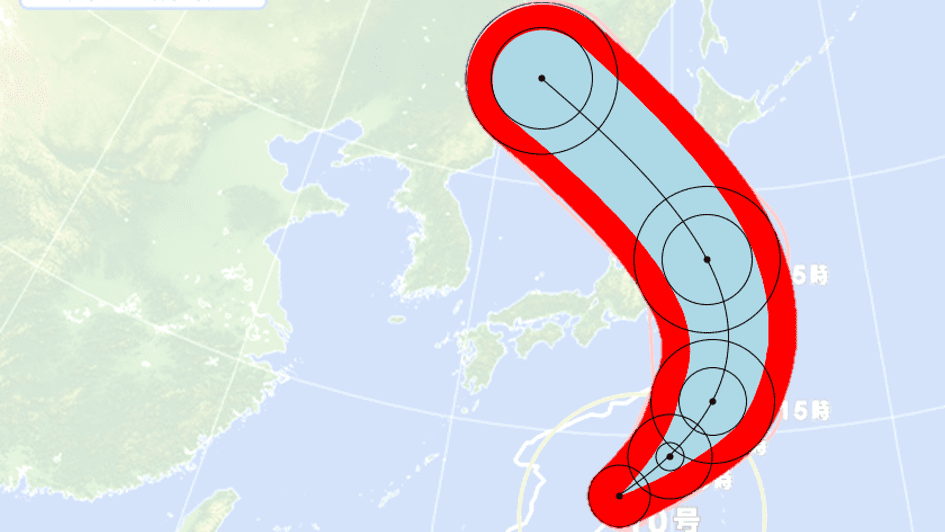
やること
台風の進路予想はなぜ直線なのでしょうか?今日は、vcoptを用いて台風の進路予想を3次関数で近似してみます。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
直線じゃないよね…?
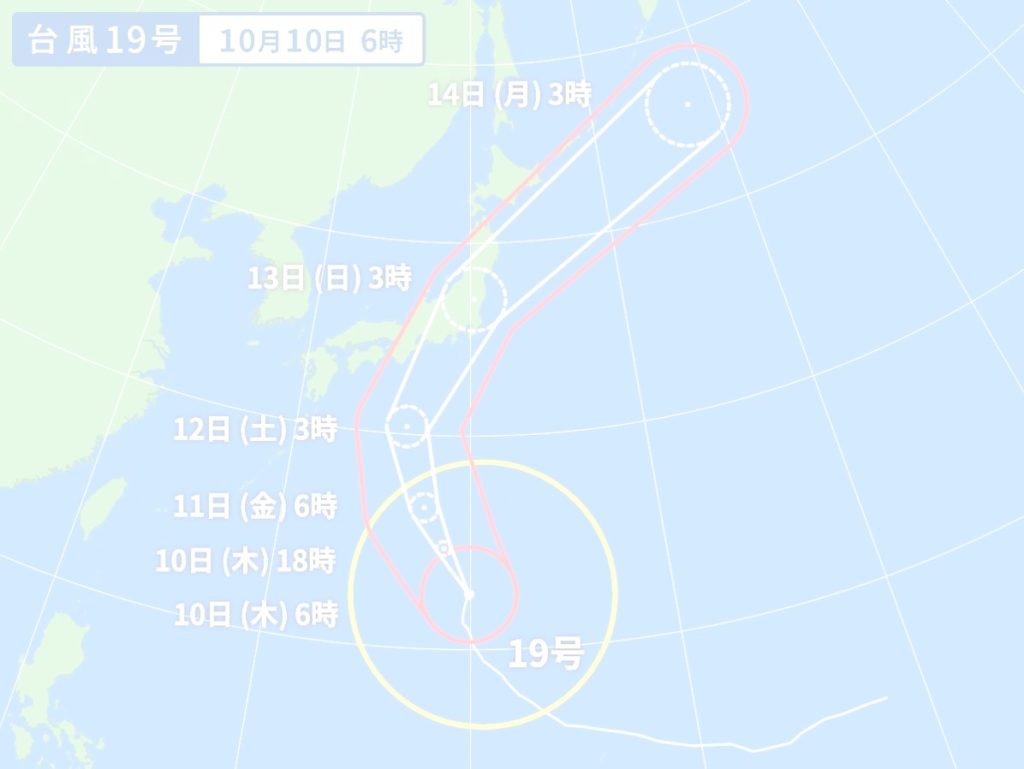
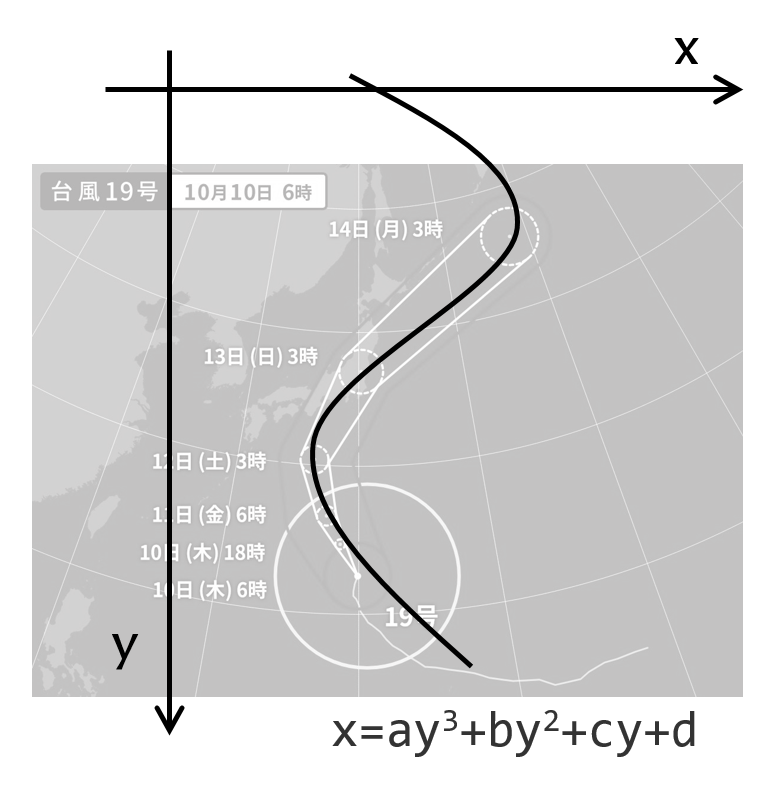
Yahoo!天気・災害によれば、2019年10月10日6時時点の台風19号の進路予想はこちらです。
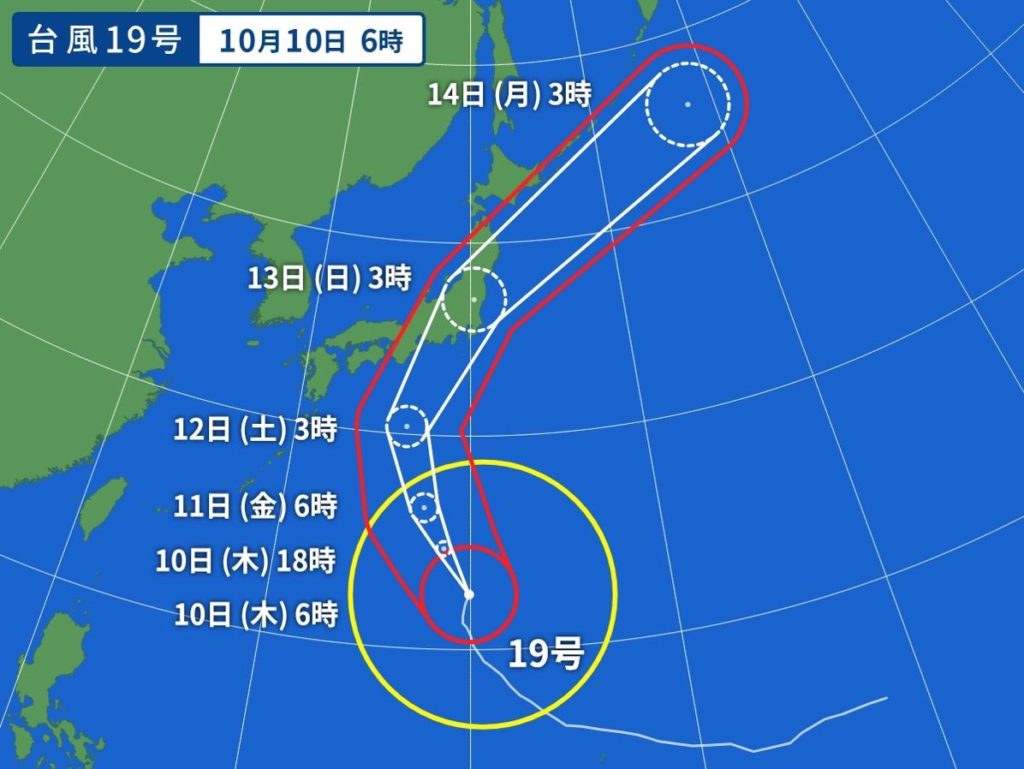
うーん、「こいつらに曲線見せてもしゃーないやろ」と思われているのでしょうか。
でもほら、こんな感じで近似できそうな気がしてきました。
進路、予報円と暴風域のサイズを決める
こちらの画像(2019_typhoon19.jpg)を用いるので、右クリック→保存してください。
プログラム冒頭のパラメータで、台風の進路、予報円と暴風域のサイズを再現します。
import numpy as np
from PIL import Image
from vcopt import vcopt
import matplotlib.pyplot as plt
#============================
# パラメータ
#============================
#地図上の座標
x = np.array([545, 495, 475, 555, 800])
y = np.array([690, 590, 500, 350, 120])
#予報円と暴風域のサイズ
yohouen = np.array([0, 25, 35, 50, 65])
bofuiki = np.array([75, 95, 80, 75, 95])
#画像ファイル
f = '2019_typhoon19.jpg'
#============================
# 間を100分割して線形に補間する
#============================
x_add = np.zeros((len(x)-1)*100)
y_add = np.zeros((len(x)-1)*100)
yohouen_add = np.zeros((len(x)-1)*100)
bofuiki_add = np.zeros((len(x)-1)*100)
for i in range(len(x) - 1):
for j in range(100):
x_tmp = (x[i] * (100 - j) + x[i+1] * j) / 100
y_tmp = (y[i] * (100 - j) + y[i+1] * j) / 100
yohouen_tmp = (yohouen[i] * (100 - j) + yohouen[i+1] * j) / 100
bofuiki_tmp = (bofuiki[i] * (100 - j) + bofuiki[i+1] * j) / 100
x_add[i*100 + j] = x_tmp
y_add[i*100 + j] = y_tmp
yohouen_add[i*100 + j] = yohouen_tmp
bofuiki_add[i*100 + j] = bofuiki_tmp
#============================
# 地図の表示
#============================
def show():
plt.figure(figsize=(15, 15)) #固定する
#地図の表示
img = Image.open(f).convert('RGB'); img.close
plt.imshow(img)
#暴風域(補完)のプロット
for i in range(len(x_add)):
plt.plot(x_add[i], y_add[i], '-ok', markersize=bofuiki_add[i], markeredgecolor='none', markerfacecolor='red', alpha=1.00)
#予報円(補完)のプロット
for i in range(len(x_add)):
plt.plot(x_add[i], y_add[i], '-ok', markersize=yohouen_add[i], markeredgecolor='none', markerfacecolor='lightblue', alpha=1.0)
#座標(補完)のプロット
plt.plot(x_add, y_add, '-k', linewidth=1)
#暴風域のプロット
for i in range(len(x)):
plt.plot(x[i], y[i], 'ok', markersize=bofuiki[i], markerfacecolor='none')
#予報円のプロット
for i in range(len(x)):
plt.plot(x[i], y[i], 'ok', markersize=yohouen[i], markerfacecolor='none')
#座標のプロット
plt.plot(x, y, 'ok', markersize=5)
plt.show()
#表示
show()たいだいこんなものでしょうか。
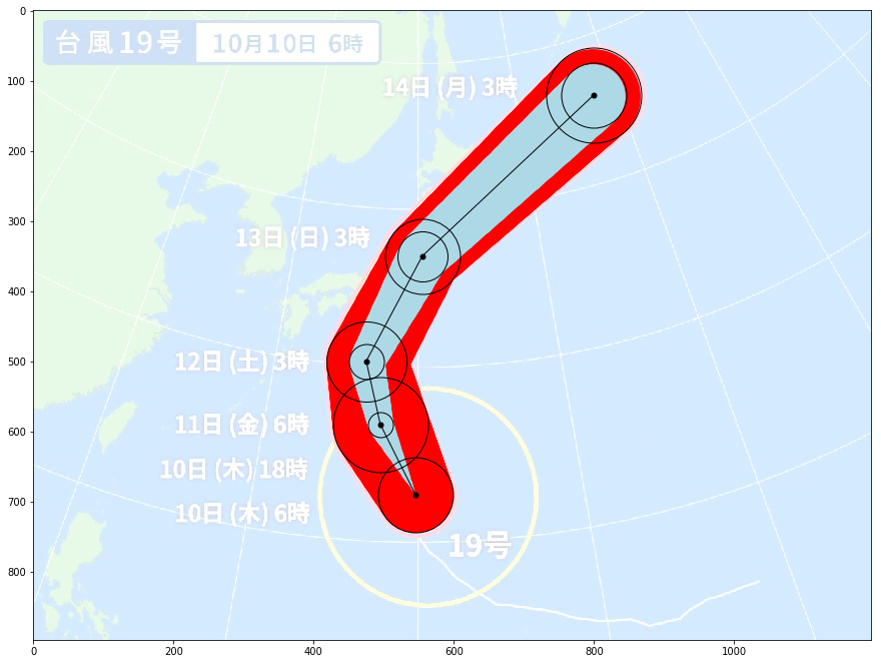
3次関数でフィッティング
vcopt().rcGA() を用いて、5つの座標を3次関数で近似します。このとき、xがyの3次関数であることに注意してください。学校で習ったのは y=ax^3+bx^2+cx+d ですが、ここでは x=ay^3+by^2+cy+d です。評価関数の返り値は、目的のx座標と算出したx座標の平均二乗誤差です。
#3次関数(ただしxがyの3次関数)
def sanji_kansu(para):
#配列のまま3次関数に通す
x_predict = para[0]*(y**3) + para[1]*(y**2) + para[2]*y + para[3]
#誤差の二乗の平均を返す
return np.mean((x - x_predict)**2)
#各パラメータの探索範囲
para_range = [[-0.1, 0.1],
[-1, 1],
[-10, 10],
[-10000, 10000]]
#GAでフィッティング
para, score = vcopt().rcGA(para_range, # パラメータ範囲
sanji_kansu, # 評価関数
0.0, # 評価関数の目標値
pool_num=2000, # 個体数を増やす
show_pool_func='print') # 表示オプション実行します。
___________________ info ___________________
para_range : n=4
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 2000
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 2000/2000
gen=0, best_score=3217431586686.621, mean_score=172331798018087.7, mean_gap=172331798018087.7, time=0.4
gen=2000, best_score=362753300.3123, mean_score=69500428850076.35, mean_gap=69500428850076.35, time=1.1
gen=4000, best_score=203541318.074, mean_score=20225021141230.203, mean_gap=20225021141230.203, time=1.5
gen=6000, best_score=72794447.7365, mean_score=4613401547041.52, mean_gap=4613401547041.52, time=1.8
.
.
.
gen=750000, best_score=20.9867, mean_score=81.5369, mean_gap=81.5369, time=119.1
gen=752000, best_score=20.9867, mean_score=81.4673, mean_gap=81.4673, time=119.4
gen=754000, best_score=20.9867, mean_score=81.3175, mean_gap=81.3175, time=119.6
gen=756000, best_score=20.9867, mean_score=81.1152, mean_gap=81.1152, time=119.9
__________________ results _________________
para : [ 0.00000144 0.00017607 -1.41334481 964.6314771 ]
score : 20.98665164883034
____________________ end ___________________平均二乗誤差が21くらいまで下がりました。良さそうです。
カーブを見てみる
「x」とそれを補完した「x_add」を、フィットした3次関数を用いて更新します。
#============================
# 間を100分割して3次関数で補間する
#============================
x = para[0]*(y**3) + para[1]*(y**2) + para[2]*y + para[3]
for i in range(len(x) - 1):
for j in range(100):
y_tmp = (y[i] * (100 - j) + y[i+1] * j) / 100
x_tmp = para[0]*(y_tmp**3) + para[1]*(y_tmp**2) + para[2]*y_tmp + para[3] # ここが変わった
yohouen_tmp = (yohouen[i] * (100 - j) + yohouen[i+1] * j) / 100
bofuiki_tmp = (bofuiki[i] * (100 - j) + bofuiki[i+1] * j) / 100
x_add[i*100 + j] = x_tmp
y_add[i*100 + j] = y_tmp
yohouen_add[i*100 + j] = yohouen_tmp
bofuiki_add[i*100 + j] = bofuiki_tmp
#表示
show()
カーブしています!
他の台風でもやってみる
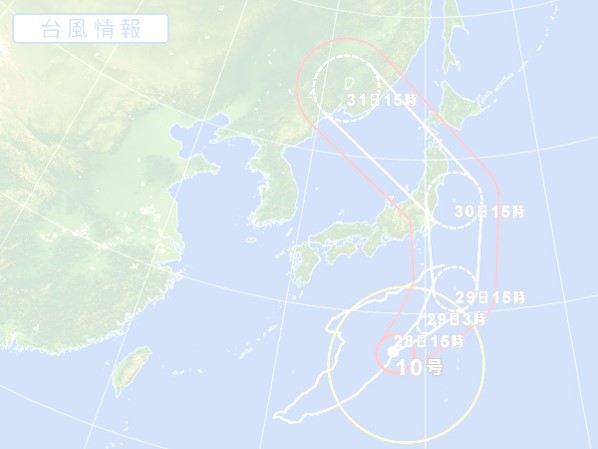
斬新な進路で世間を賑わせた、2016年の台風10号でも試してみます。
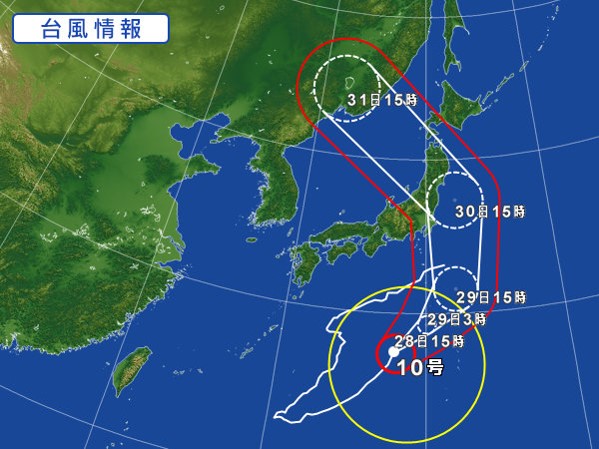
こちらをダウンロードして用いてください。
#============================
# パラメータ
#============================
#地図上の座標
x = np.array([395, 425, 455, 450, 345])
y = np.array([350, 325, 290, 200, 85])
#予報円と暴風域のサイズ
yohouen = np.array([0, 25, 60, 80, 90])
bofuiki = np.array([55, 75, 110, 130, 135])
#画像ファイル
f = '2016_typhoon10.jpg'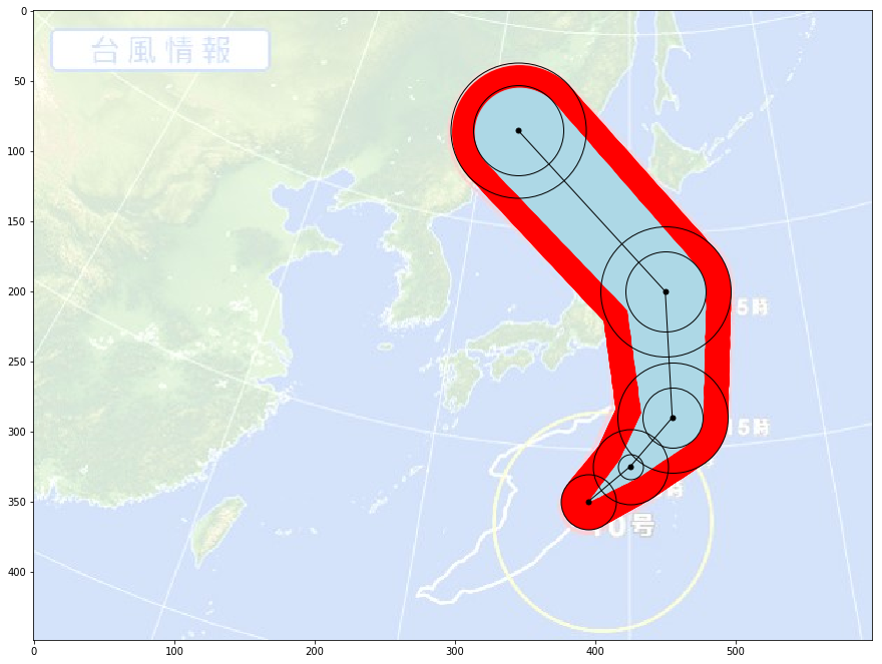
___________________ info ___________________
para_range : n=4
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 2000
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 2000/2000
gen=0, best_score=51970610330.8003, mean_score=3736413919611.128, mean_gap=3736413919611.128, time=0.4
gen=2000, best_score=12544382.9878, mean_score=1496703640652.8335, mean_gap=1496703640652.8335, time=1.1
gen=4000, best_score=12544382.9878, mean_score=382630739017.8471, mean_gap=382630739017.8471, time=1.4
gen=6000, best_score=3065087.0677, mean_score=94961798439.965, mean_gap=94961798439.965, time=1.8
.
.
.
gen=670000, best_score=0.6626, mean_score=12.6764, mean_gap=12.6764, time=113.4
gen=672000, best_score=0.6626, mean_score=12.6691, mean_gap=12.6691, time=113.8
gen=674000, best_score=0.6626, mean_score=12.6536, mean_gap=12.6536, time=114.1
gen=676000, best_score=0.6626, mean_score=11.6674, mean_gap=11.6674, time=114.4
__________________ results _________________
para : [-9.84367032e-06 1.38390252e-03 1.15505210e+00 2.42695946e+02]
score : 0.6626203048034978
____________________ end ___________________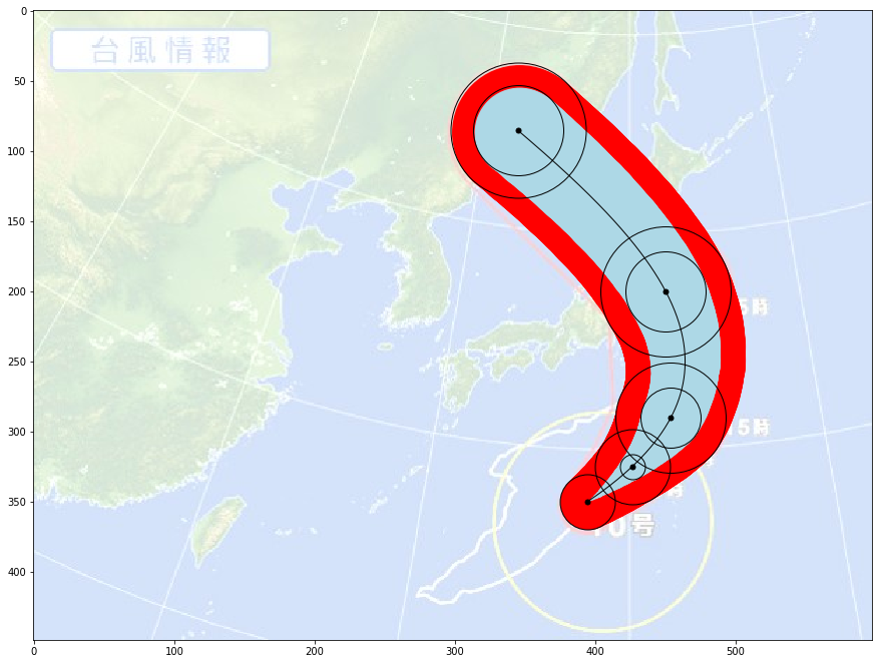
ほとんど誤差なく、美しくカーブしました。