やること
いまポケモンは809種類いるらしいです。あれ？251匹くらいじゃありませんでした？と言うとだいたいの年齢がバレます。ポケモンバトルでは３対３がスタンダードだそうですので、できるだけ多くのポケモンに有利が取れる３匹を、遺伝的アルゴリズムを使って選出してみましょう。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
sourceforge.net
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
ポケモンのデータベース
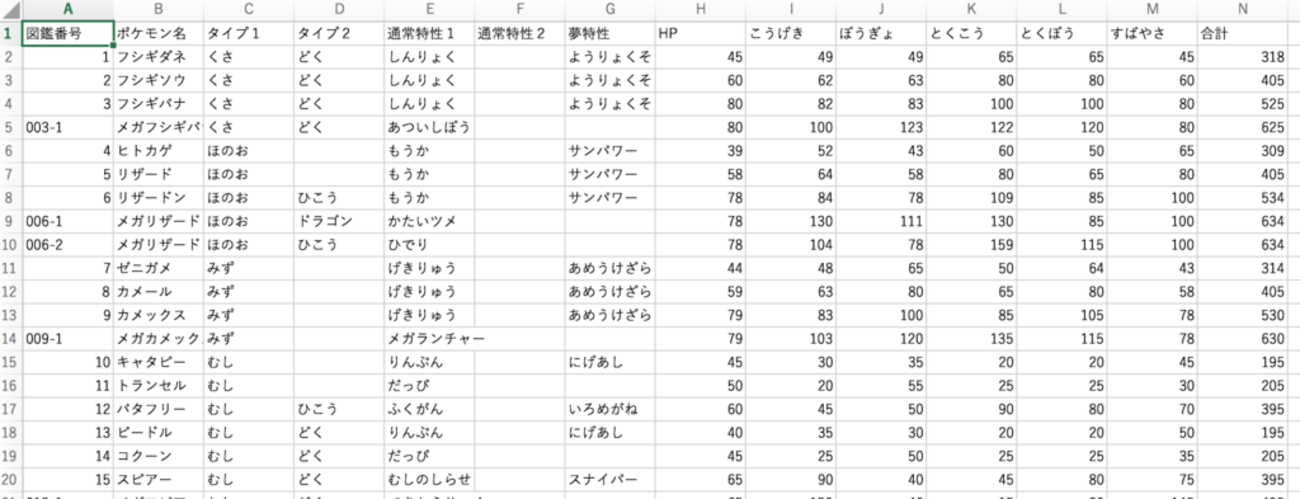
全ポケモンのデータベースはこちらを使わせていただきました。
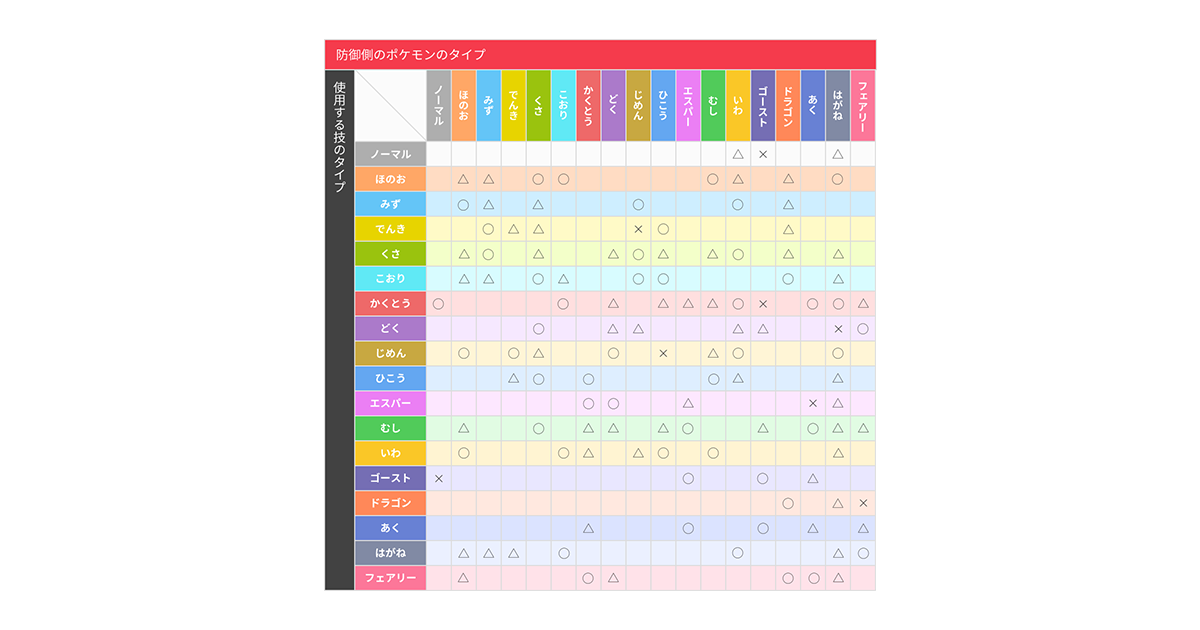
タイプ別相性表は公式のものを使わせていただきました。（え、フェアリータイプなんてあるの！？）
バトルに役立つ！ タイプ相性表を公開！｜『ポケットモンスター サン・ムーン』公式サイト
『ポケットモンスター サン・ムーン』公式サイト。『ポケットモンスター』シリーズ最新作。『ポケットモンスター サン・ムーン』、ニンテンドー3DSで、2016年11月18日（金）、世界で発売！
www.pokemon.co.jp
最強の３匹の定義
３匹を選出し、全ポケモンに対して攻撃させて、「こうかばつぐん」が取れる相手の数をスコアとします。つまり、できるだけ多種類のポケモンに対応可能な万能チームを最強とします。
簡単のために、３匹は自分がもつタイプの攻撃を行うとし、お互いの「とくせい」などは考慮しません。めざパ氷とかもありません。
pip, import
今回はグラフ中で日本語を表示したいので、こちらをpipします。
pip install japanize-matplotlib今回使うパッケージをインポートします。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from vcopt import vcopt全ポケモンデータの読み込み
上の「pokemon_status.csv」の全行、２～４列目を読み込みます。
#============================
#全ポケモンデータの読み込み
#============================
#ファイル名
file = open('pokemon_status.csv', 'r')
#
data = []
#１行目はラベルなのでカラ読み
label = file.readline().split(',')[1:4]
#２行目以降を読み込む
while 1:
tmp = file.readline().split(',')[1:4]
if len(tmp) > 1:
data.append(tmp)
else:
break
file.close()
print('ポケモンの数:{}'.format(len(data)))
print('ラベル:{}'.format(label))
print('ポケモンID=0:{}'.format(data[0]))
print('ポケモンID=4:{}'.format(data[4]))
print('ポケモンID=9:{}'.format(data[9]))ポケモンの数:841
ラベル:['ポケモン名', 'タイプ１', 'タイプ２']
ポケモンID=0:['フシギダネ', 'くさ', 'どく']
ポケモンID=4:['ヒトカゲ', 'ほのお', '']
ポケモンID=9:['ゼニガメ', 'みず', '']あれ、841匹います。メガシンカを含んでいるのでしょうか？841匹から３匹を選ぶ組み合わせ総数は98,783,860通りです。
タイプ別相性表の用意
おそろしいことに手入力です。注意点として、タイプを１つしかもたないポケモンは、データベース上ではタイプ２が ” という感じで空のタイプをもっていますので、相性表も空のタイプに対応させています。
#============================
#タイプ相性表
#============================
table = {'':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':1.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':1.0,'フェアリー':1.0},
'ノーマル':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':1.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':0.5,'ゴースト':0.0,'ドラゴン':1.0,'あく':1.0,'はがね':0.5,'フェアリー':1.0},
'ほのお':{'':1.0,'ノーマル':1.0,'ほのお':0.5,'みず':0.5,'でんき':1.0,'くさ':2.0,'こおり':2.0,'かくとう':1.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':2.0,'いわ':0.5,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':2.0,'フェアリー':1.0},
'みず':{'':1.0,'ノーマル':1.0,'ほのお':2.0,'みず':0.5,'でんき':1.0,'くさ':0.5,'こおり':1.0,'かくとう':1.0,'どく':1.0,'じめん':2.0,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':2.0,'ゴースト':1.0,'ドラゴン':0.5,'あく':1.0,'はがね':1.0,'フェアリー':1.0},
'でんき':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':2.0,'でんき':0.5,'くさ':0.5,'こおり':1.0,'かくとう':1.0,'どく':1.0,'じめん':0.0,'ひこう':2.0,'エスパー':1.0,'むし':1.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':0.5,'あく':1.0,'はがね':1.0,'フェアリー':1.0},
'くさ':{'':1.0,'ノーマル':1.0,'ほのお':0.5,'みず':2.0,'でんき':1.0,'くさ':0.5,'こおり':1.0,'かくとう':1.0,'どく':0.5,'じめん':2.0,'ひこう':0.5,'エスパー':1.0,'むし':0.5,'いわ':2.0,'ゴースト':1.0,'ドラゴン':0.5,'あく':1.0,'はがね':0.5,'フェアリー':1.0},
'こおり':{'':1.0,'ノーマル':1.0,'ほのお':0.5,'みず':0.5,'でんき':1.0,'くさ':2.0,'こおり':0.5,'かくとう':1.0,'どく':1.0,'じめん':2.0,'ひこう':2.0,'エスパー':1.0,'むし':1.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':2.0,'あく':1.0,'はがね':0.5,'フェアリー':1.0},
'かくとう':{'':1.0,'ノーマル':2.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':2.0,'かくとう':1.0,'どく':0.5,'じめん':1.0,'ひこう':0.5,'エスパー':0.5,'むし':0.5,'いわ':2.0,'ゴースト':0.0,'ドラゴン':1.0,'あく':2.0,'はがね':2.0,'フェアリー':0.5},
'どく':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':2.0,'こおり':1.0,'かくとう':1.0,'どく':0.5,'じめん':0.5,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':0.5,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':0.0,'フェアリー':2.0},
'じめん':{'':1.0,'ノーマル':1.0,'ほのお':2.0,'みず':1.0,'でんき':2.0,'くさ':0.5,'こおり':1.0,'かくとう':1.0,'どく':2.0,'じめん':1.0,'ひこう':0.0,'エスパー':1.0,'むし':0.5,'いわ':2.0,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':2.0,'フェアリー':1.0},
'ひこう':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':0.5,'くさ':2.0,'こおり':1.0,'かくとう':2.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':2.0,'いわ':0.5,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':0.5,'フェアリー':1.0},
'エスパー':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':2.0,'どく':2.0,'じめん':1.0,'ひこう':1.0,'エスパー':0.5,'むし':1.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':1.0,'あく':0.0,'はがね':0.5,'フェアリー':1.0},
'むし':{'':1.0,'ノーマル':1.0,'ほのお':0.5,'みず':1.0,'でんき':1.0,'くさ':2.0,'こおり':1.0,'かくとう':0.5,'どく':0.5,'じめん':1.0,'ひこう':0.5,'エスパー':2.0,'むし':1.0,'いわ':1.0,'ゴースト':0.5,'ドラゴン':1.0,'あく':2.0,'はがね':0.5,'フェアリー':0.5},
'いわ':{'':1.0,'ノーマル':1.0,'ほのお':2.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':2.0,'かくとう':0.5,'どく':1.0,'じめん':0.5,'ひこう':2.0,'エスパー':1.0,'むし':2.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':0.5,'フェアリー':1.0},
'ゴースト':{'':1.0,'ノーマル':0.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':1.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':2.0,'むし':1.0,'いわ':1.0,'ゴースト':2.0,'ドラゴン':1.0,'あく':0.5,'はがね':1.0,'フェアリー':1.0},
'ドラゴン':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':1.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':2.0,'あく':1.0,'はがね':0.5,'フェアリー':0.0},
'あく':{'':1.0,'ノーマル':1.0,'ほのお':1.0,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':0.5,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':2.0,'むし':1.0,'いわ':1.0,'ゴースト':2.0,'ドラゴン':1.0,'あく':0.5,'はがね':1.0,'フェアリー':0.5},
'はがね':{'':1.0,'ノーマル':1.0,'ほのお':0.5,'みず':0.5,'でんき':0.5,'くさ':1.0,'こおり':2.0,'かくとう':1.0,'どく':1.0,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':2.0,'ゴースト':1.0,'ドラゴン':1.0,'あく':1.0,'はがね':0.5,'フェアリー':2.0},
'フェアリー':{'':1.0,'ノーマル':1.0,'ほのお':0.5,'みず':1.0,'でんき':1.0,'くさ':1.0,'こおり':1.0,'かくとう':2.0,'どく':0.5,'じめん':1.0,'ひこう':1.0,'エスパー':1.0,'むし':1.0,'いわ':1.0,'ゴースト':1.0,'ドラゴン':2.0,'あく':2.0,'はがね':0.5,'フェアリー':1.0}}
print(table['ほのお']['くさ'])2.0table[‘ほのお’][‘くさ’] は「ほのお→くさ」の攻撃を意味し、ダメージ倍率2.0が返ってきます。
（必須）評価関数
ポケモンIDが３つ並んだparaを受け取って、全ポケモンへの攻撃を行い、「こうかばつぐん」が取れる数を返します。
#評価関数
def pokemon_score(para):
#攻撃ポケモン３匹
attacker_1 = data[para[0]]
attacker_2 = data[para[1]]
attacker_3 = data[para[2]]
#841匹に対する「こうかばつぐん」を記録する
data_mask = np.zeros(len(data), dtype=bool)
for i in range(len(data)):
#防御ポケモン
defender = data[i]
#攻撃ポケモン１について
#（攻撃タイプ１ → 防御タイプ１） × （攻撃タイプ１ → 防御タイプ２）
if table[attacker_1[1]][defender[1]] * table[attacker_1[1]][defender[2]] >= 2.0:
#こうかばつぐんならTrueを記録
data_mask[i] = True
#（攻撃タイプ２ → 防御タイプ１） × （攻撃タイプ２ → 防御タイプ２）
if table[attacker_1[2]][defender[1]] * table[attacker_1[2]][defender[2]] >= 2.0:
#こうかばつぐんならTrueを記録
data_mask[i] = True
#攻撃ポケモン２について
if table[attacker_2[1]][defender[1]] * table[attacker_2[1]][defender[2]] >= 2.0:
data_mask[i] = True
if table[attacker_2[2]][defender[1]] * table[attacker_2[2]][defender[2]] >= 2.0:
data_mask[i] = True
#攻撃ポケモン３について
if table[attacker_3[1]][defender[1]] * table[attacker_3[1]][defender[2]] >= 2.0:
data_mask[i] = True
if table[attacker_3[2]][defender[1]] * table[attacker_3[2]][defender[2]] >= 2.0:
data_mask[i] = True
#効果抜群が取れるポケモン数を返す
return np.sum(data_mask)
print(pokemon_score([0, 4, 9]))502試しにpara=[0, 4, 9]（フシギダネ、ヒトカゲ、ゼニガメ）の３匹を入れてみると、502が返ってきました。841匹中の502匹に対して「こうかばつぐん」が取れるという意味です。あれ、マサラタウンの３匹だけでそこそこのカバー力がありますね。
（任意）すべてのパラメータ群を可視化する関数
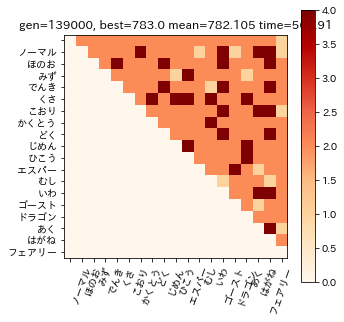
poolを受け取って、エリート個体（＝現時点の最強３匹）を全タイプの組み合わせに対して攻撃させます。もっとも高いダメージ倍率をヒートマップにします。まあ…伝われ（諦め）。
#poolの可視化
def pokemon_show_pool(pool, **info):
#任意で次の変数が使用できます
gen = info['gen']
best_index = info['best_index']
best_score = info['best_score']
mean_score = info['mean_score']
mean_gap = info['mean_gap']
time = info['time']
#攻撃ポケモン３匹
attacker_1 = data[pool[best_index, 0]]
attacker_2 = data[pool[best_index, 1]]
attacker_3 = data[pool[best_index, 2]]
#全タイプ
name = ['', 'ノーマル','ほのお','みず','でんき','くさ','こおり','かくとう','どく','じめん','ひこう','エスパー','むし','いわ','ゴースト','ドラゴン','あく','はがね','フェアリー']
#全タイプの組み合わせに対して３匹で攻撃し、ダメージ倍率を記録する（上三角行列になる）
table_mask = np.zeros((len(name), len(name)))
for i in range(len(name)):
for j in range(i + 1, len(name)):
#攻撃ポケモン１について
#（攻撃タイプ１ → 防御タイプ１） × （攻撃タイプ１ → 防御タイプ２）
rate = table[attacker_1[1]][name[i]] * table[attacker_1[1]][name[j]]
if rate > table_mask[i, j]:
table_mask[i, j] = rate
#（攻撃タイプ２ → 防御タイプ１） × （攻撃タイプ２ → 防御タイプ２）
rate = table[attacker_1[2]][name[i]] * table[attacker_1[2]][name[j]]
if rate > table_mask[i, j]:
table_mask[i, j] = rate
#攻撃ポケモン２について
rate = table[attacker_2[1]][name[i]] * table[attacker_2[1]][name[j]]
if rate > table_mask[i, j]:
table_mask[i, j] = rate
rate = table[attacker_2[2]][name[i]] * table[attacker_2[2]][name[j]]
if rate > table_mask[i, j]:
table_mask[i, j] = rate
#攻撃ポケモン３について
rate = table[attacker_3[1]][name[i]] * table[attacker_3[1]][name[j]]
if rate > table_mask[i, j]:
table_mask[i, j] = rate
rate = table[attacker_3[2]][name[i]] * table[attacker_3[2]][name[j]]
if rate > table_mask[i, j]:
table_mask[i, j] = rate
#エリートチームを表示
print(data[pool[best_index, 0]], data[pool[best_index, 1]], data[pool[best_index, 2]])
#ヒートマップで表示
plt.figure(figsize=(8, 8))
plt.imshow(table_mask, vmin=-4, vmax=4, cmap='bwr')
plt.xticks(range(len(name)), name)
plt.xticks(rotation=70)
plt.yticks(range(len(name)), name)
plt.title('gen={}, best={} mean={} time={}'.format(gen, best_score, mean_score, time))
#plt.savefig('save/{}.png'.format(gen))
plt.show()
print()GAで最適化
GAを実行します。
#パラメータ範囲
para_range = [[i for i in range(0, len(data))] for j in range(3)]
#GAで最適化
para, score = vcopt().dcGA(para_range, #para_range
pokemon_score, #score_func
9999, #aim
show_pool_func=pokemon_show_pool, #show_para_func=None
seed=None, #seed=None
pool_num=200)
#結果の表示
print(data[para[0]])
print(data[para[1]])
print(data[para[2]])
print(score)実行結果
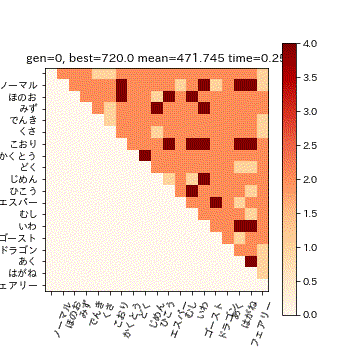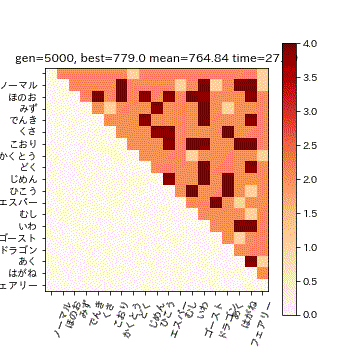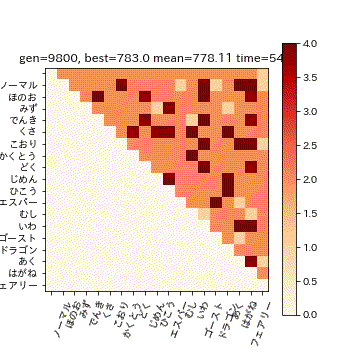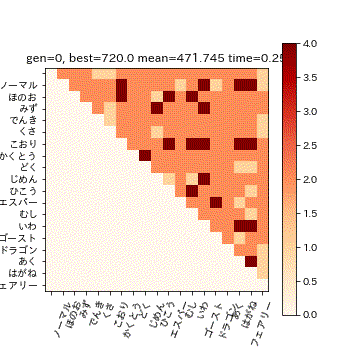
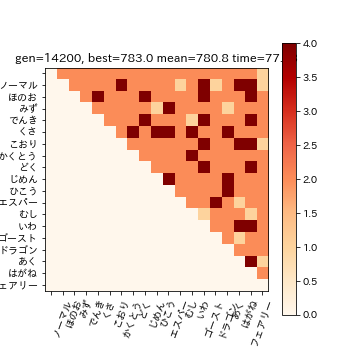
['ロトム飛', 'でんき', 'ひこう']
['ケケンカニ', 'かくとう', 'こおり']
['ゴルーグ', 'じめん', 'ゴースト']
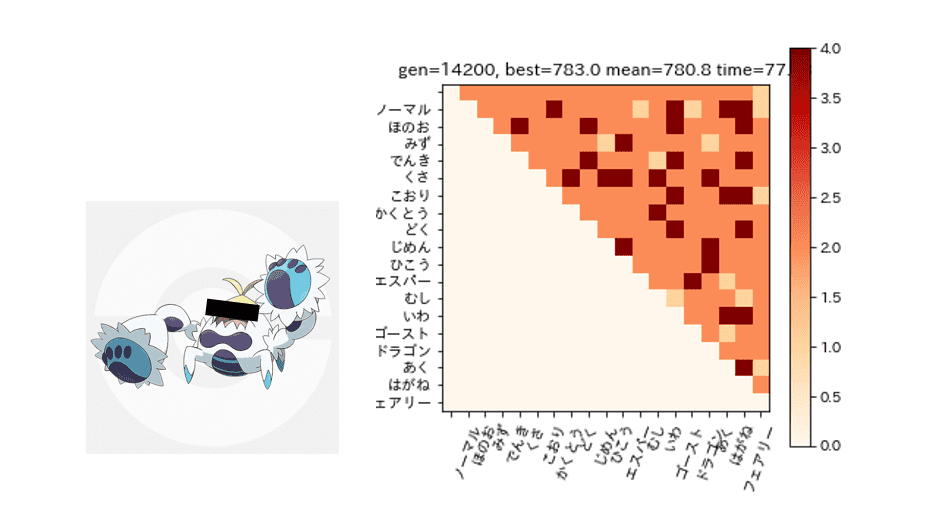
783.0ということで、こちらの３匹で809匹中783匹に対応できることが分かりました。
扇風機 スピンロトム、カニ ケケンカニ、 マッハのスピードで空を飛ぶと言われている素早さ種族値55のゴーレム ゴルーグ
またこの３匹では、ヒートマップ中の1.0倍の部分のタイプには対応できません。例えば、フェアリー単タイプに対しては「どく」か「はがね」が必要ですが、３匹とももっていません。
このような感じで、技も考慮して本当の最強３匹を選出するとかやってみたいですね。
追伸
何回か実行すると、次の解も出てきました。
['テラキオン', 'いわ', 'かくとう']
['オーロット', 'ゴースト', 'くさ']
['イノムー', 'こおり', 'じめん']
783.0
