やること
最近、新型コロナウイルスの感染対策として、1人1人が社会的距離をとることが重視されています。そこで今回はある部屋に複数の人がいたとき、どのように配置すれば社会的距離を確保できるか遺伝的アルゴリズムで最適化してみます。今回は社会的距離を2m(200px)とします。
以下のように机(灰色)が配置されている部屋を想定します。比較として机が何もない部屋も検証します。なお机の中に書かれている文字は左上の起点の座標を意味します。

部屋0 
部屋1 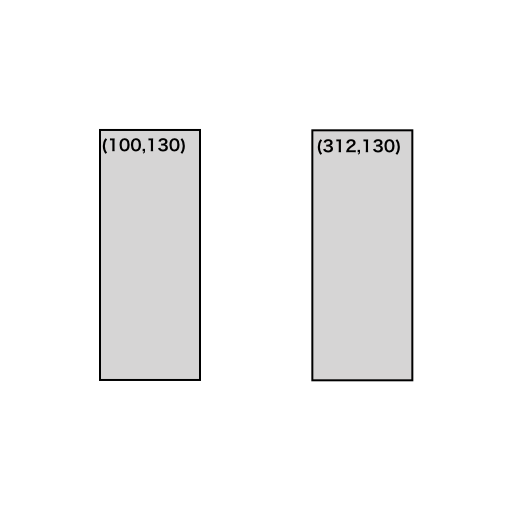
部屋2

部屋3 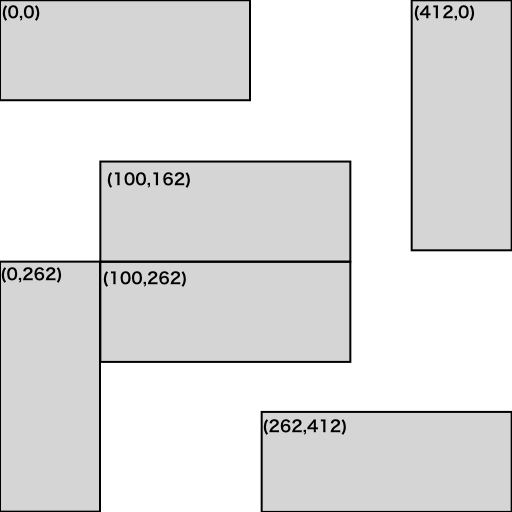
部屋4 
実行環境
Google Colaboratoryが利用可能です。

vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
pip, import
vcoptをインストールします。
pip install vcopt#================================
# プロット関連のimport
#================================
import matplotlib.pyplot as plt
from PIL import Image, ImageDraw
#================================
# その他のimport
#================================
import numpy as np
import numpy.random as nr
from copy import deepcopy
#================================
# vcopt関連のimport
#================================
from vcopt import vcopt配置図の読み込み
#================================
# 配置図の読み込み
#================================
img = Image.open('001.png').convert('RGB')
w, h = img.size
print('w, h\n{}, {}'.format(w, h))
plt.imshow(img)
plt.show()
plt.close()制約条件となる関数
机の上や壁の中には人を配置することができないので、200px以下に近づいている場合に比べてdenseの増加量を大きくしました。
#部屋に配置された机の領域には人を配置しないようにする
def constraint1(para,rad,start,hw):
dense =0
#hw=[x,y]
for p in para:
#x方向の制約条件
c1 = (start[0]-rad<= p[0]) and (p[0]<=start[0]+hw[0]+rad)
#y方向の制約条件
c2 = (start[1]-rad<= p[1]) and (p[1]<=start[1]+hw[1]+rad)
#この領域にparaの要素がが存在する場合、denseに+1をしていく
if c1 and c2:
dense +=2
return dense#壁から一定の範囲内には人を配置しないようにする
def constraint2(para,rad,hw):
dense =0
y = hw[0]#縦方向
x = hw[1]#横方向
for p in para:
#x方向の制約条件
c1 = (p[0]<=rad) or (x-rad<=p[0])
#y方向の制約条件
c2 = (p[1]<=rad) or (y-rad<=p[1])
#この領域にparaの要素がが存在する場合、denseに+1をしていく
if c1 or c2:
dense +=2
return dense評価関数
#================================
# 評価関数
#================================
def score_func(para, plot=False):
#paraを人の座標に変形し[よこ, たて]、int形式にする
position = para.reshape((-1, 2))
#半径30くらいは人の体と判断する
position[:, 0] *= w
position[:, 1] *= h
position = np.array(position, dtype=int)
#print(position)
#plotオプションがTrueなら
if plot:
#配置図に人をプロットして表示
img_tmp = deepcopy(img)
draw = ImageDraw.Draw(img_tmp)
for w_station, h_station in position:
draw.ellipse((w_station-30, h_station-30, w_station+30, h_station+30), fill=None, outline=(255, 0, 0))
#表示
plt.imshow(img_tmp)
plt.show()
plt.close()
#距離が200px以下であれば+1していく
dense = 0
#制約条件
#部屋によって変更する部分(ここでは部屋1)
#constraint1(パラメーター、半径, 左上の起点、領域の[幅、高さ])
#constraint1(para,rad,start,hw):
dense += constraint1(position, 30, [100,130],[100,250])
dense += constraint1(position, 30, [312,130],[100,250])
#constraint2(パラメーター、半径,画像の[幅、高さ])
#constraint2(para,rad,hw)
dense += constraint2(position,30,[512,512])
for i in range(len(position)):
#stationの値を1~nまで順番に入れていく
origin = position[i]
# for j in range(len(position)):
for j in list(range(i+1,len(position))):
#2点間の距離を出す
num = ((position[j, 0]-origin[0])**2 + (position[j, 1]-origin[1])**2)**0.5
if num<=200:
dense+=1
#denseの数を少なくするように最適化していく
return denseGAで最適化
#================================
# GAで最適化
#================================
#パラメータ範囲
para_range = np.zeros((8, 2))
para_range[:, 1] = 1
print(para_range)
#GAの実行
para, score = vcopt().rcGA(para_range, #パラメータ範囲
score_func, #評価関数
0.0, #目標値
show_pool_func='print', #GAの表示オプション
max_gen=50000) #最大進化世代数
#結果の確認
score_func(para, True)何もない部屋で検証
画像ファイル名は'000.png'とします。以後、別の部屋のレイアウトで検証する場合、ここのファイル名を変更します。
#================================
# 配置図の読み込み
#================================
img = Image.open('000.png').convert('RGB')
w, h = img.size
print('w, h\n{}, {}'.format(w, h))
plt.imshow(img)
plt.show()
plt.close()今回、机を配置しないので制約条件は壁から一定の距離には人を配置しない、という条件だけになります。それは以下の部分になります。これはすべての検証を通して変更しない制約条件です。
#constraint2(パラメーター、半径,画像の[幅、高さ])
#constraint2(para,rad,hw)
dense += constraint2(position,30,[512,512]) 次に人数を変更していきます。変更する場合はnp.zeros((8, 2))の部分を変更します。この場合は4人分の位置情報を最適化する設定となります。8人分にしたい場合はnp.zeros((16, 2))というようにします。
#パラメータ範囲
para_range = np.zeros((8, 2))
para_range[:, 1] = 1
print(para_range)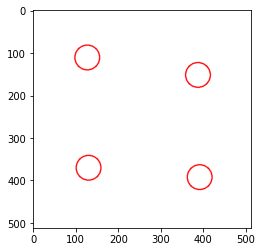
4人 
5人 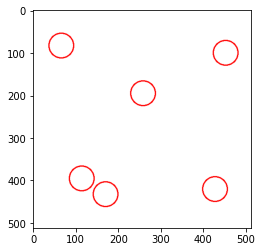
6人
4人は余裕で入ります。5人も余裕です、しかし、6人目になると、200pxの距離は保つことが難しくなり、密な部分が出てしまっています。
部屋1で検証
画像ファイル名は'001.png'とし、制約条件は以下のようにします。
#001
dense += constraint1(position, 30, [216,131],[100,250])
4人 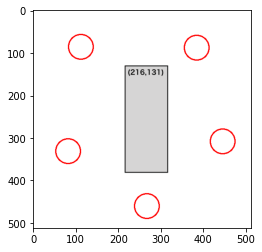
5人 
6人
何もない部屋では中央に人が配置されていましたが、中央に机があると、このように人を配置することで社会的距離を確保できるようになりました。何もない部屋と同様、6人はやはり無理です。
部屋2で検証
画像ファイル名は'002.png'とし、制約条件は以下のようにします。
#部屋によって変更する部分(ここでは部屋1)
#constraint1(パラメーター、半径, 左上の起点、領域の[幅、高さ])
#constraint1(para,rad,start,hw):
dense += constraint1(position, 30, [100,130],[100,250])
dense += constraint1(position, 30, [312,130],[100,250])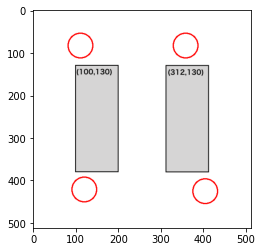
4人 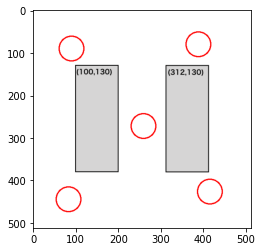
5人 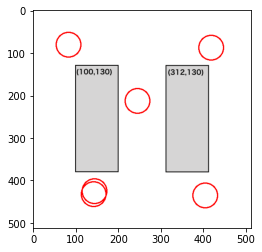
6人
部屋1は机ありですが、中央にスペースがあるので、机を置かない場合とほとんど変わらない配置になりました。
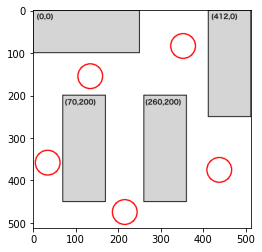
部屋3で検証
画像ファイル名は'vcopt003.png'とし、制約条件は以下のようにします。
#003
dense += constraint1(position, 30, [0,0],[250,100])
dense += constraint1(position, 30, [412,0],[100,250])
dense += constraint1(position, 30, [70,200],[100,250])
dense += constraint1(position, 30, [260,200],[100,250])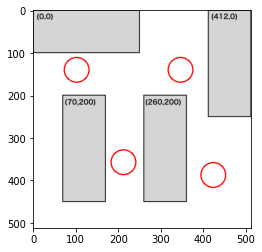
4人 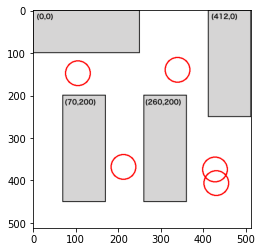
5人 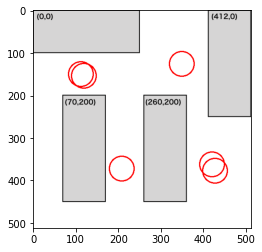
6人
部屋2に比べて机の配置がやや複雑になってきます。5人目の時点ですでに密な部分ができてしまっています。左下の部分にもスペースがあるのでいけそうな気がしますが、壁から一定のスペースには配置しないという制約(constraint2)が効いているのか、そこに人を配置しないように最適化されているようです。試しに、constraint2の制約を緩めてみましょう。以下のようにconstrain2関数のdenseの増加量を+2→+1にしてみます。
#壁から一定の範囲内には人を配置しないようにする
def constraint2(para,rad,hw):
dense =0
y = hw[0]#縦方向
x = hw[1]#横方向
for p in para:
#x方向の制約条件
c1 = (p[0]<=rad) or (x-rad<=p[0])
#y方向の制約条件
c2 = (p[1]<=rad) or (y-rad<=p[1])
#この領域にparaの要素がが存在する場合、nearに+1をしていく
if c1 or c2:
#ここを+=2 -> +=1に変更する
dense +=1
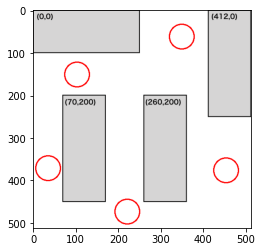
return dense壁際に関する制約を緩めると以下のように配置が変化しました。確率的な最適化であるため、毎回微妙に位置が変わってきていますが、今度は壁際の狭いスペースにも人が配置されるようになっています。密な部分もできず5人を配置することができました。
部屋4で検証
画像ファイル名は'vcopt004.png'とし、制約条件は以下のようにします。
#004
dense += constraint1(position, 30, [0,0],[250,100])
dense += constraint1(position, 30, [412,0],[100,250])
dense += constraint1(position, 30, [0,262],[100,250])
dense += constraint1(position, 30, [100,162],[250,100])
dense += constraint1(position, 30, [100,262],[250,100])
dense += constraint1(position, 30, [260,412],[250,100])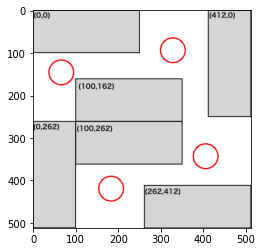
4人 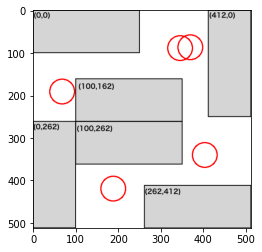
5人 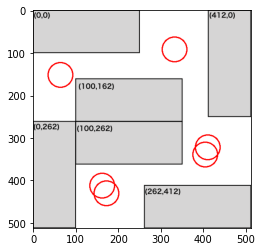
6人
最後の部屋はより複雑な配置になります。直感的にも4人が限界だと思ったのですが、実際に最適化してみてもやはり4人が限界でした。ちなみにこちらも壁際の制約を緩めて最適化してみましたが、この部屋の結果は変わりませんでした。また机の領域の制約(constraint1関数)も緩めてみましたが、結果は同じでした。この机配置では4人までが限界のようです。
まとめ
512cm×512cmの部屋では5人までならば、社会的距離を確保しつつ、人を配置できることがわかりました。しかしながら、それ以上の人数になると何もない部屋であっても密な状態の人が1人以上存在するようになります。また、この人数は机の配置によっても変化し、複雑な机の配置であれば4人までになりました。