やること
以前書いたチューリング・パターンの記事の閲覧数が地味に伸びています。
記事中の「線の生成」を見ていたら、何かひらめきました。
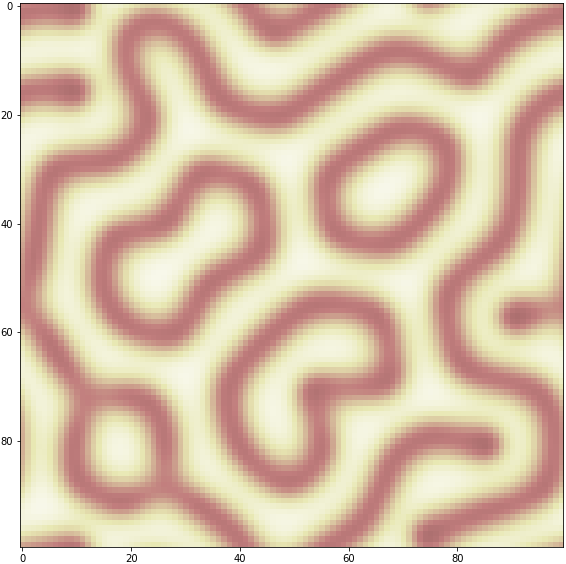
一筆書きのパズルが解けるのでは?
何を言っているか分からないかと思いますが、行ってみましょう。今回はチューリング・パターンを応用して一筆書きパズル(Fill puzzle)を解いてみます。
Fill パズルとは
一般名称なのか商標なのか、よく分かりませんがこんなパズルです。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

そもそも、できるのか?
とりあえず実現可能性を見てみます。前記事の「線の生成」のパラメータを少し修正して、
- 条件1:線の先端が伸びる
- 条件2:線の腹も伸びる
- 条件3:線が分岐しない(Y字ができない)
を満たすギリギリのパラメータを見つけました。条件2と3は相反するのでバランスが難しかったです。線の腹は伸びてほしいのですが、油断すると酵母みたいにプリッと出芽してY字路ができます。Y字路ができてしまっては一筆書きになりませんからね。
※ちなみにこのパラメータでも稀に出芽します。条件2を少し優先したためです。
また境界条件として、外枠を固めてトーラスにならないようにしました。
import numpy as np
import numpy.random as nr
from scipy import signal
import matplotlib.pyplot as plt
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 90, 90
#終了ステップ数
max_step = 10000
#拡散係数
D1 = 0.2
D2 = 0.1
#線の生成(分岐せず腹移動するギリギリのライン)
f = 0.063
k = 0.0638
#============================
#メイン処理
#============================
#フィールドの初期化
u = np.ones((h, w))
v = np.zeros((h, w))
#初期状態の設定
size = 6
#中央に乱数の正方形
u[h//2-size//2:w//2+size//2, h//2-size//2:w//2+size//2] = nr.rand(size, size)
v[h//2-size//2:w//2+size//2, h//2-size//2:w//2+size//2] = nr.rand(size, size)
#畳み込み用のフィルタ
g = np.array([[0.00, 1.00, 0.00],
[1.00, -4.0, 1.00],
[0.00, 1.00, 0.00]])
#表示
plt.figure()
plt.imshow(u, cmap='pink', vmin=0, vmax=1)
plt.show(), plt.close(), print()
#状態の更新
for i in range(1, max_step + 1):
#拡散項(u, vを畳み込んでdu, dvとする)
du = signal.convolve2d(u, g, mode='same',boundary='wrap') * D1
dv = signal.convolve2d(v, g, mode='same',boundary='wrap') * D2
#du, dvに反応項を加える
du = du - (u * v*v) + f*(1.0 - u)
dv = dv + (u * v*v) - (f + k)*v
#フィールドの更新(オイラー法)
u += du
v += dv
#外枠を固める
u[:, :1] = 0.4
u[:1, :] = 0.4
u[:, -1:] = 0.4
u[-1:, :] = 0.4
#表示
if i % 300 == 0:
plt.figure(figsize=(8, 8))
plt.imshow(u, cmap='pink', vmin=0, vmax=1)
plt.show(), plt.close(), print()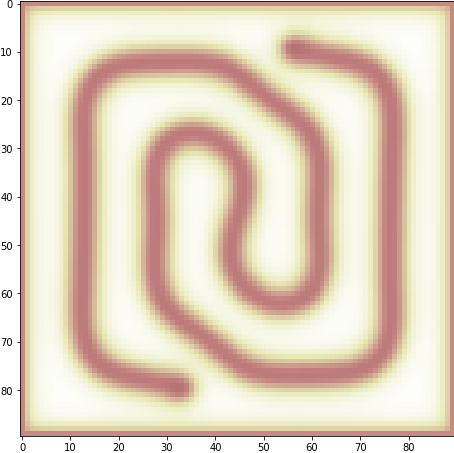
ムニムニして気持ちいですね。なんとなく行けそうだということが分かりました。
問題1
ネット上から拝借した5×5サイズの問題に挑戦します。解答は一意ではありません。

問題を反映するため「左上からn番目の区画を壁にする関数」を用意して、外枠を壁にする作業と同様に毎ステップ実行しました。
import numpy as np
import numpy.random as nr
from scipy import signal
import matplotlib.pyplot as plt
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 90, 90
#終了ステップ数
max_step = 10000
#拡散係数
D1 = 0.2
D2 = 0.1
#線の生成(分岐せず腹移動するギリギリのライン)
f = 0.063
k = 0.0638
#============================
#メイン処理
#============================
#フィールドの初期化
u = np.ones((h, w))
v = np.zeros((h, w))
#初期状態の設定
size = 6
#中央に乱数の正方形
u[h//2-size//2:w//2+size//2, h//2-size//2:w//2+size//2] = nr.rand(size, size)
v[h//2-size//2:w//2+size//2, h//2-size//2:w//2+size//2] = nr.rand(size, size)
#畳み込み用のフィルタ
g = np.array([[0.00, 1.00, 0.00],
[1.00, -4.0, 1.00],
[0.00, 1.00, 0.00]])
#表示
plt.figure()
plt.imshow(u, cmap='pink', vmin=0, vmax=1)
plt.show(), plt.close(), print()
#左上からn番目の区画を壁にする関数(n=0~24)
def block(u, n):
x = n // 5
y = n % 5
l = w // 5
u[l*x+1:l*(x+1)-1, l*y+1:l*(y+1)-1] = 0.4
return u
#状態の更新
for i in range(1, max_step + 1):
#拡散項(u, vを畳み込んでdu, dvとする)
du = signal.convolve2d(u, g, mode='same',boundary='wrap') * D1
dv = signal.convolve2d(v, g, mode='same',boundary='wrap') * D2
#du, dvに反応項を加える
du = du - (u * v*v) + f*(1.0 - u)
dv = dv + (u * v*v) - (f + k)*v
#フィールドの更新(オイラー法)
u += du
v += dv
#外枠を固める
u[:, :1] = 0.4
u[:1, :] = 0.4
u[:, -1:] = 0.4
u[-1:, :] = 0.4
#左上からn番目の区画を壁にする
u = block(u, 2)
u = block(u, 3)
u = block(u, 17)
u = block(u, 20)
u = block(u, 24)
#表示
if i % 300 == 0:
plt.figure(figsize=(8, 8))
plt.imshow(u, cmap='pink', vmin=0, vmax=1)
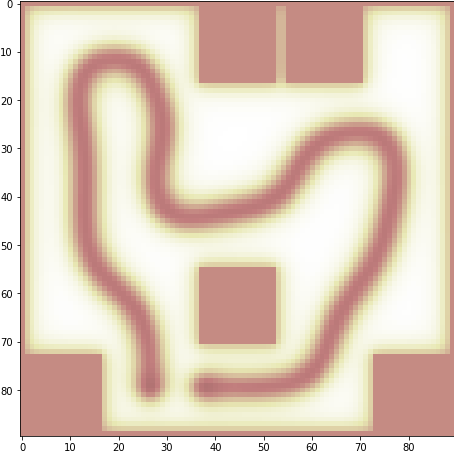
plt.show(), plt.close(), print()失敗例
成功例
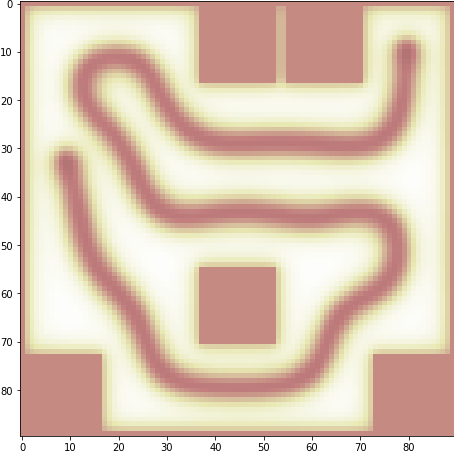
良いんじゃないでしょうか!?ちょっと空気を読んで補正してやれば、パズルの解答として十分に成立します!
問題2
こちらもネット上から拝借した6×6サイズの問題。

6×6用に一部書き換えます。フィールドサイズはけっこう微妙なパラメータなので問題によっては要調整です。
#高さ、幅
h, w = 105, 105#左上からn番目の区画を壁にする関数(n=0~24)
def block(u, n):
x = n // 6
y = n % 6
l = w // 6
u[l*x+1:l*(x+1)-1, l*y+1:l*(y+1)-1] = 0.4
return u #左上からn番目の区画を壁にする
u = block(u, 0)
u = block(u, 4)
u = block(u, 13)
u = block(u, 19)
u = block(u, 30)失敗例1
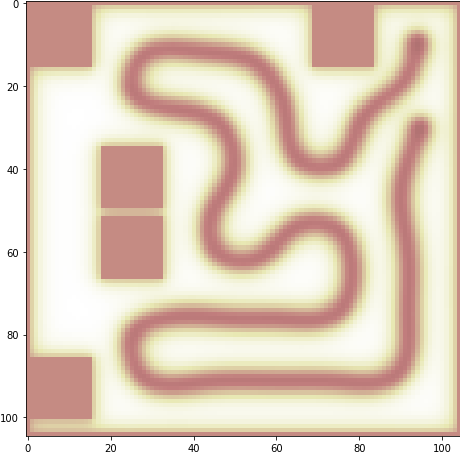
失敗例2

成功例
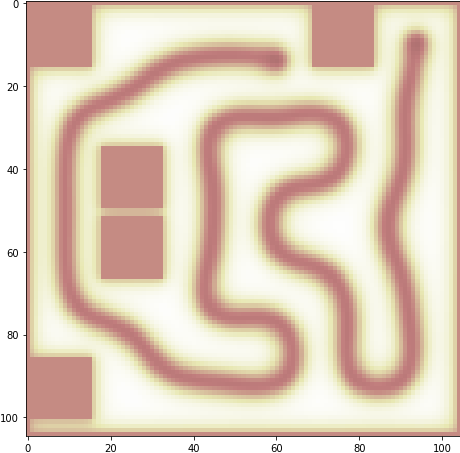
成功率は低いですが、解けましたね?解けてますよねこれ?(再確認。。)
まとめ
フィールドサイズが大きくなるほど成功率が下がります。というのは、パラメータを調整して「線の幅=マスの幅」にしているのですが、広い空間内では線の自由度が高く、両者の幅が食い違ってくるからです(伝われ!)。フィールドサイズのパラメータが微妙であることも同じ理由です。
ですからもっと壁が多い(自由度が低い)問題であれば安定的に対応できるかもしれません。ただ、自由度が低い=問題として簡単であるため、結局のところあまり役に立たない解法かもしれません。。


