やること
最近、ジェンダーギャップ指数という単語をよく聞くようになりました。スイスの世界経済フォーラム(World Economic Forum : WEF)が毎年公表しており、各国の男女格差を数値化しランキングにしたものです。約150ヶ国がリストアップされる中で日本は2020年121位、2021年120位となっており、「男女同権化が進んでいない」根拠として頻繁に取り上げられています。
しかしこの主張に対しては、ジェンダーギャップ指数の元となる4つの指標(経済、教育、健康、政治)の性質上、日本にとって不利な統計が取られているという指摘があります。ここではきちんとソースを確認しながら、日本が不利にならないように偏差値や標準化を用いてランキングを洗い直してみます。
参考文献
WEFのレポートはこちらから見られます。
元データのcsvやExcelは日本語の検索では見つかりませんでした。いろいろ頑張ってcsvを整えたので置いておきます。
後半で使うロジット関数についてはこちらをご参考ください。
ジェンダーギャップ指数と統計のはなし
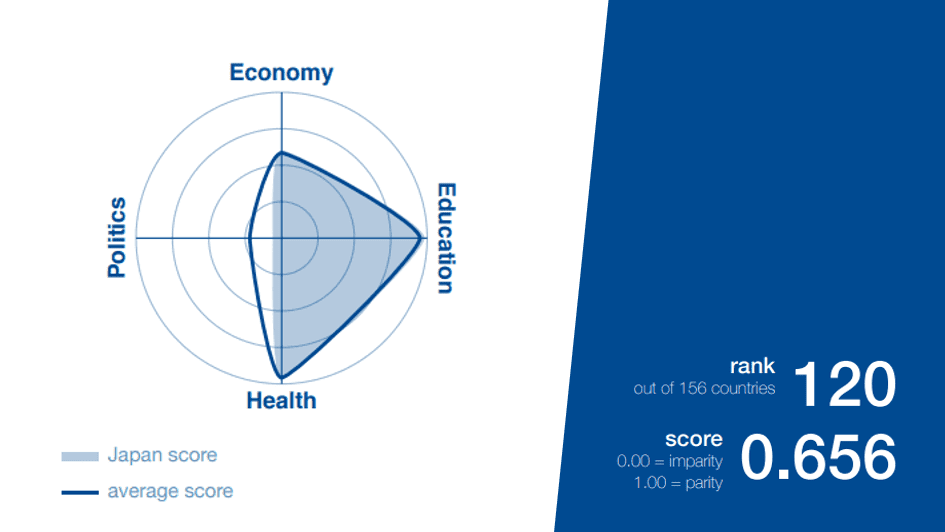
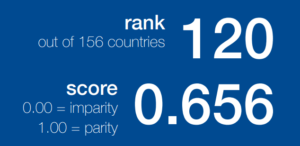
WEFのレポートによれば、日本のジェンダーギャップ指数は156ヶ国中120位と非常に低い順位です。

0.656という総合点は4つの部門点(経済、教育、健康、政治)の平均値です。部門点を見ると経済(117位)と政治(147位)が足を引っ張っていることがわかり、レポートでは女性の収入が男性の60%程度しかないことや、過去50年間に女性総理大臣が一人もいなかったことが指摘されています。一方で、教育(0.983点)と健康(0.973点)はほとんど満点であり、義務教育を受ける機会の男女格差がほとんどないことが称賛されています。
しかし、上のレーダーチャートのaverage scoreを見ると、教育と健康はどちらも世界平均が約95点であり差がつきにくい状況です。日本はいわば「得意科目で差をつけづらく、苦手科目でしっかり差がつく」テストを受けているようなものだという指摘があります。
これはテストを設計した人が悪いです。平均点が95点って接待ですか?どの教科も平均60点くらいに設計してくれなければ実力差を適切に測定することができません。そこで、各国の点数を偏差値にしたり補正(標準化)したりして、どの教科のパワーバランスも等しくしてから改めて日本の順位を見てみようという話になるわけです。

余談ですが、先日の共通テストは数ⅠAの平均点が大きく下がり、「数学が得意な人にとって不利だった」なんて言われています。
データの読み込み
csvデータを読み込んで、4つの指標を取得できていることを確認します。
import numpy as np
import numpy.random as nr
import pandas as pd
from copy import deepcopy
import matplotlib.pyplot as plt
#データ読み込み
data = pd.read_csv('Global Gender Gap Subindex 2021.csv', encoding='utf-8', header=0)
#国名
data_country = np.array(data['Country Name'])
print('data_country[:5] = {}'.format(data_country[:5]))
#4指標を抽出
data_health = np.array(data['Global Gender Gap Health and Survival Subindex'])
data_education = np.array(data['Global Gender Gap Educational Attainment Subindex'])
data_economy = np.array(data['Global Gender Gap Economic Participation and Opportunity Subindex'])
data_politics = np.array(data['Global Gender Gap Political Empowerment subindex'])
print('data_health[:5] = {}'.format(data_health[:5]))
print('data_education[:5] = {}'.format(data_education[:5]))
print('data_economy[:5] = {}'.format(data_economy[:5]))
print('data_politics[:5] = {}'.format(data_politics[:5]))
#4指標を結合したもの
four = np.stack([data_health, data_education, data_economy, data_politics], axis=1)
#nanのある行を除く
country = data_country[~np.isnan(four).any(axis=1)]
four = four[~np.isnan(four).any(axis=1)]data_country[:5] = ['Afghanistan' 'Albania' 'Algeria' 'Angola' 'Argentina']
data_health[:5] = [0.952 0.956 0.958 0.976 0.977]
data_education[:5] = [0.514 0.999 0.966 0.759 1. ]
data_economy[:5] = [0.18 0.748 0.456 0.646 0.639]
data_politics[:5] = [0.132 0.377 0.151 0.245 0.39 ]4指標の散布図
4指標の散布図を出してみます。
#4指標の散布図の関数
def show_scatter(country, four):
jpidx = np.where(country=='Japan')[0][0]
for i in range(4):
plt.scatter(nr.randn(len(four))/50+i, four[:, i], color='k', s=2)
plt.scatter([i], four[jpidx, i], color='r', marker='_', s=1000) #日本を赤線で
plt.xticks(range(4), ['health', 'education', 'economy', 'politics'])
plt.show()
plt.close()
#4指標の散布図
show_scatter(country, four)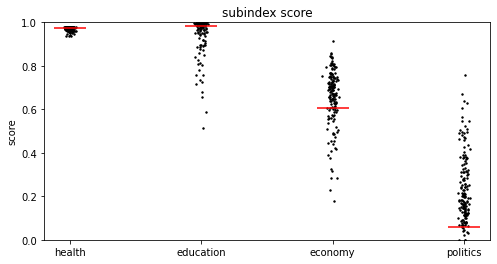
赤線は日本の位置を示しています。たしかに、健康と教育がほとんど皆カンストしているのに対し、経済と政治は比較的広く分布しています。絶対評価だから仕方がないということでしょうか?それとも、「健康と教育はガチでクレーム来るからみんな100点にしとこう。他は低くてもいいか。」という思惑なのでしょうか?
次に、4指標を平均してジェンダーギャップ指数(GGGI)のランキングを出してみます。
#ランキングの関数
def show_rank(country, val):
#nanを除く
c = country[~np.isnan(val)]
v = val[~np.isnan(val)]
#大きい順にソート
idx = np.argsort(v)[::-1]
c_sort = c[idx]
v_sort = v[idx]
jpidx = np.where(c_sort=='Japan')[0][0]
print('japan rank = {}'.format(jpidx))
#ベスト10とワースト10
plt.subplot(121)
plt.bar(range(10), v_sort[:10], color='gray', tick_label=c_sort[:10])
plt.subplot(122)
plt.bar(range(10), v_sort[-10:], color='gray', tick_label=c_sort[-10:])
plt.show()
plt.close()
#4指標の平均でジェンダーギャップ指数を計算
GGGI = np.mean(four, axis=1)
print('GGGI[:5] = {}'.format(GGGI[:5]))
#ランキングを表示
show_rank(country, GGGI)GGGI[:5] = [0.4445 0.77 0.63275 0.6565 0.7515 ]
japan rank = 120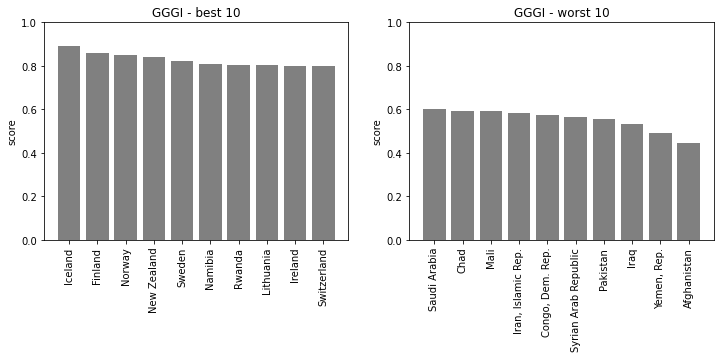
日本は120位と算出され、WEFのレポートと一致しました。
4指標をそれぞれ偏差値にしてみる
では、学力テストでもよく見る偏差値にしてみてはどうでしょうか。4指標をそれぞれ偏差値に変換してから散布図とランキングを出してみます。
#4指標をそれぞれ偏差値にしてから散布図
four2 = deepcopy(four)
for i in range(4):
four2[:, i] = 50 + 10 * (four2[:, i] - np.average(four2[:, i])) / np.std(four2[:, i])
show_scatter(country, four2)
#これでジェンダーギャップ指数を計算
GGGI_standard = np.mean(four2, axis=1)
print('GGGI_standard[:5] = {}'.format(GGGI_standard[:5]))
#ランキングを表示
show_rank(country, GGGI_standard)GGGI_standard[:5] = [21.1705082 51.59715048 41.91055118 45.73514797 55.42146072]
japan rank = 109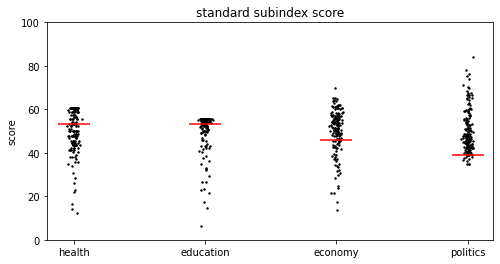

どうでしょうか。日本のジェンダーギャップ偏差値は109位です。偏差値にしたことで山が50点付近に来ましたが、どうも正規分布に見えません。元がある程度正規分布でなければ偏差値にしても正規分布にはならないのですね。
4指標をそれぞれロジット関数に通してから偏差値にしてみる
さて、ここで2つの関数を勉強します。
シグモイド関数
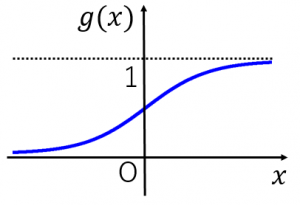
シグモイド関数はマイナス無限からプラス無限までどんな数を入れても0~1の間に押し込めてくれます。深層学習の活性化関数としても使われています(どんな値になっても次の層には0~1で渡してあげたいから)。
ロジット関数
ロジット関数はシグモイド関数の逆関数で、0~1の値をマイナス無限からプラス無限に展開したいときに使えます(さっきと逆のことを言っているだけです)。ただ注目したいのは、0付近や1付近にぎゅっと集まっている点群をファサっと開いてくれるカーブをしているところです。これを利用すれば0.95点付近で密になっている健康と教育の点をいい感じに散らせるのです。
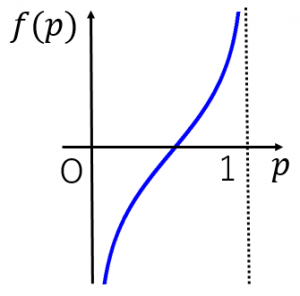
ロジット関数を適用してみる
#4指標をロジット関数に通してから散布図
four3 = deepcopy(four)
for i in range(4):
#0除算回避
four3[:, i] = np.clip(four3[:, i], 0.001, 0.999)
#ロジット関数
four3[:, i] = np.log(four3[:, i] / (1 - four3[:, i]))
show_scatter(country, four3)
#これでジェンダーギャップ指数を計算
GGGI_logit = np.mean(four3, axis=1)
print('GGGI_logit[:5] = {}'.format(GGGI_logit[:5]))
#ランキングを表示
show_rank(country, GGGI_logit)GGGI_logit[:5] = [-0.08908965 2.6427489 1.14268642 1.08216416 2.69486537]
japan rank = 111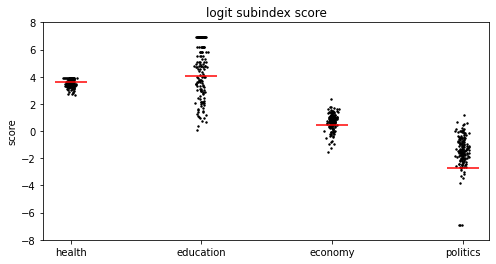

ロジット関数に通したことで当初より健全な分布になったように見えます。日本はロジットジェンダーギャップ指数で111位まで上がりました!
さらに偏差値にしてみる
four4 = deepcopy(four3)
for i in range(4):
#偏差値
four4[:, i] = 50 + 10 * (four3[:, i] - np.average(four3[:, i])) / np.std(four3[:, i])
show_scatter(country, four4)
#これでジェンダーギャップ指数を計算
GGGI_logit_standard = np.mean(four4, axis=1)
print('GGGI_logit_standard[:5] = {}'.format(GGGI_logit_standard[:5]))
#ランキングを表示
show_rank(country, GGGI_logit_standard)GGGI_logit_standard[:5] = [29.66993965 52.89487215 40.92859231 47.53691477 56.51405356]
japan rank = 114
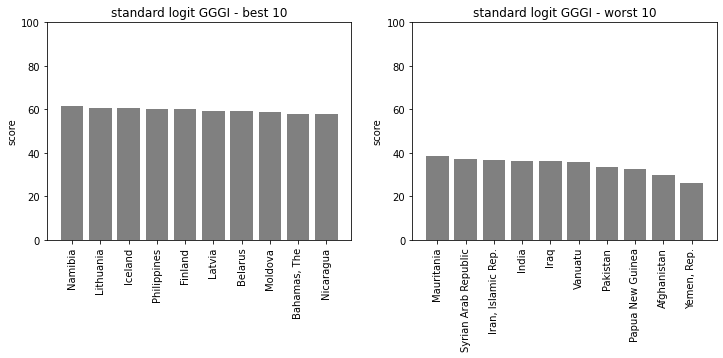
偏差値にすると少し下がって、ロジットジェンダーギャップ偏差値は114位になりました。とはいえ今までで一番まともな分布に見えます。
結論
今回の検証では偏差値や標準化を駆使しても日本の順位はさほど上がりませんでした。よく考えれば当然なのですが、もともと教育(92位)も健康(65位)も高いわけではなく、(相対的には)得意科目ではなかったのです。我々は何を勘違いしていたのでしょうか。
今回分かったことは、
日本のジェンダーギャップ指数は120位
日本のジェンダーギャップ偏差値は109位
日本のロジットジェンダーギャップ指数は111位
日本のロジットジェンダーギャップ偏差値は114位
どうやっても低かったです。
数値の補正について言えば、多くの人にとって分かりやすい指標を作るならば、あまり数字をこねくり回すのは良くないでしょう。だからといって単に「平均値でいっか」では統計のマジックが起きます。平均値か中央値かでさえ議論になるのですから。

余談ですが、陸上競技の「十種競技」はご存知でしょうか。例えば100m走のタイムは25.4347×(18-T)^1.81といった感じでミッチミチに補正します。究極の相対評価ですね。