はじめに
前編ではAさんの研究の悪かった点として「対照群(コントロール)がない」「現役教員へのヒアリング方法が適切でない」ことを挙げました。早速これらを検証・検討してみましょう。
コントロール実験
コントロールの設計
Aさんは「既存のデータを解析する場合は今更コントロール実験なんてできないでしょ」と思っていましたが、生徒たちの対照実験はできなくても解析方法のコントロールはできます。それは、「解析手法をランダムデータに適用するとどれくらいの大問が抽出されるか」を調べることです。ランダムデータ(無意味なデータ)でも同じように5問くらい抽出されるようであれば、Aさんの結果は意味があるか甚だ疑問になってしまいますので、願わくば1問も抽出されてほしくありません。さっそくやってみましょう。
コントロール実験(Pythonで)
生徒数100、大問数500、t検定の有意水準を1%とします。高1時の500問のスコア(各20点満点)を正規分布で生成します。また、入学した大学(学部)の偏差値も正規分布で生成します。これらはまったく無意味なデータです。
import numpy as np
import numpy.random as nr
import scipy.stats as stats
import matplotlib.pyplot as plt
#乱数シード
nr.seed(0)
#パラメータ
num_student = 100
num_question = 500
p_border = 0.01
#高校1年時の様々なテストの大問スコア
ko1_score = (nr.randn(num_student, num_question) * 3 + 12).astype(int)
ko1_score = np.clip(ko1_score, 0, 20)
#確認
print(ko1_score.shape)
plt.hist(ko1_score.flatten(), bins=range(0, 21, 1))
plt.xlim(0, 20)
plt.show()
#入学大学(学部)の偏差値
hensachi = (nr.randn(num_student) * 9 + 50).astype(int)
hensachi = np.clip(hensachi, 25, 75)
#確認
print(hensachi.shape)
plt.hist(hensachi, bins=range(0, 101, 5))
plt.xlim(0, 100)
plt.show()(100, 500)
(100,)高1時の大問のスコアはこのような分布に
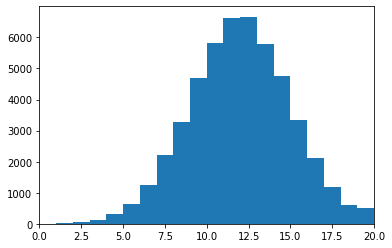
入学した大学(学部)の偏差値はこのような分布に(ちょっと正規分布に見えないですが)
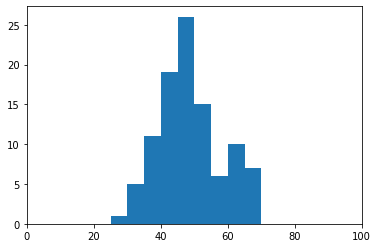
次に、「高偏差値集団」と「低偏差値集団」のマスクを作成します。
#大学偏差値が高い人のマスク、低い人のマスク
high_mask = (hensachi >= 60)
print(np.sum(high_mask))
low_mask = (hensachi <= 40)
print(np.sum(low_mask))
#大学偏差値が高い人の大問スコア、低い人の大問スコア
ko1_score_high = ko1_score[high_mask]
print(ko1_score_high.shape)
ko1_score_low = ko1_score[low_mask]
print(ko1_score_low.shape)17
19
(17, 500)
(19, 500)それぞれ17人、19人いました。Aさんの実データでは20人ずついたので同じくらいと考えていいでしょう。
最後に、各大問でt検定を行い、「高偏差値集団」と「低偏差値集団」でスコアに有意差があった大問を見つけます。グラフ化の関数にちょっとこだわりました。
#ヒストグラム関数
def show(data1, data2, size=6):
plt.hist(data1, bins=range(0, 21, 1), alpha=0.3, density=True, color='green', label='high hensachi daigaku')
plt.hist(data2, bins=range(0, 21, 1), alpha=0.5, density=True, color='orange', label='low hensachi daigaku')
#確率密度
def gauss(x, mu, sigma):
return np.exp(-(x - mu)**2/(2*sigma**2)) / (2*np.pi*sigma**2)**0.5
#最尤推定でフィット曲線
mu, sigma = np.mean(data1), np.std(data1)
x_ = np.arange(0, 20, 0.001)
y_ = gauss(x_, mu, sigma)
plt.plot(x_, y_, color='green')
mu, sigma = np.mean(data2), np.std(data2)
x_ = np.arange(0, 20, 0.001)
y_ = gauss(x_, mu, sigma)
plt.plot(x_, y_, color='orange')
plt.xlim(0, 20)
plt.xlabel('ko1 daimon score')
plt.legend()
plt.show()
#全問題を調べる
for i in range(num_question):
#対応のないt検定、等分散仮定
t, p = stats.ttest_ind(ko1_score_high[:, i], ko1_score_low[:, i], equal_var=True)
#有意差あり、highのほうが高平均なら表示
if p < p_border and t > 0:
print('i={}, p={}'.format(i, round(p, 4)))
print('high mean={}, low mean={}'.format(round(np.mean(ko1_score_high[:, i]), 1), round(np.mean(ko1_score_low[:, i]), 1)))
show(ko1_score_high[:, i], ko1_score_low[:, i])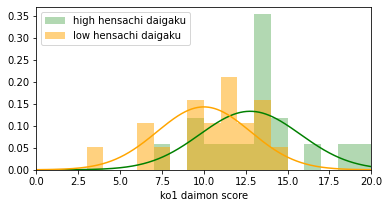
high mean=12.8, low mean=10.0
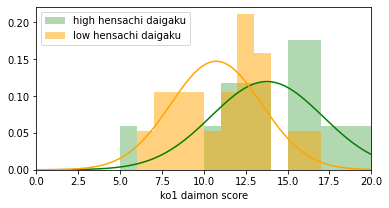
high mean=13.8, low mean=10.7
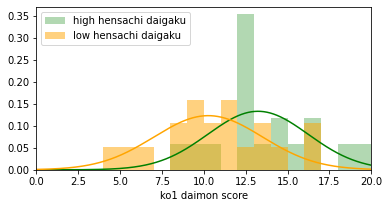
high mean=13.2, low mean=10.3
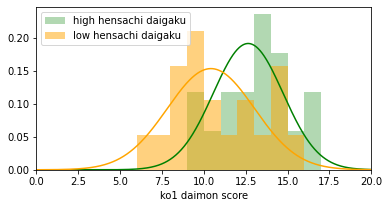
high mean=12.6, low mean=10.4
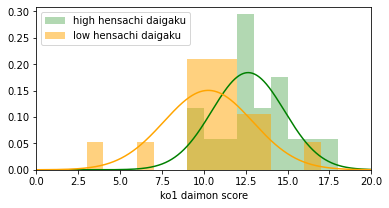
high mean=12.6, low mean=10.3
500問中5問に有意差がありました。
結論
結局、ランダムで無意味なデータを用いても5問が抽出されました。もちろん乱数シードを変えると抽出数は変わります。
荒削りではありますが、こんなに短いコードで、わずか数秒間待つだけで、コントロール実験が1つできました。結論、「Aさんが実データから5問を抽出したことは意味があるとは思えない」と分かり、違う切り口で解析をしていく必要があることになります。
現役教員へのヒアリング方法
Aさんは「現役の高校教員3名に研究の趣旨を伝え、5問にどのような共通点があるかを自由記述形式で質問」しました。
これの良くないところは、「どのような共通点がありますか?」と聞いた点です。そう聞かれれば頑張って共通点を探そうとしますし、探せば何か共通点は見つかるものです。極端な話、国語の漢字書き取りの問題と数学の二次関数のグラフを描かせる問題でも、「問題文を読んで適切な線を書く力」とか言えるわけです。
そういったバイアスを生みそうな情報は事前に与えるべきではありませんし、もっと言えば、コントロールとして無関係な問題を数問混ぜてヒアリングを行い、抽出された5問だけに共通する特徴があったかどうかを解析するべきです。高校教員の負担は増えますが、それは余計な負担ではなく「実験に必要な負担」と考えるべきです。

えー、なんか思っていた研究方法と違う!エレガントじゃない!

研究とはそういうものです。
さいごに
最近、中高生から自由研究の相談を受けることが増えてきました。HPの記事を見てメールやSlackで技術的な点を質問してくださるのですが、話を聞いてみるとそもそも実験設計が良くないこともあったりします。私たちは全員が修士・博士卒業者なので、研究は楽しく聞かせていただきますし、時間があるときであれば一緒に議論します。(秘密は守りますが、他の人と共同で行っている研究の相談は十分にご注意ください)


