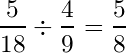はじめに
条件付き確率(じょうけんつきかくりつ、英:conditional probability)は、ある事象Bが起こると言う条件下での別の事象Aの確率のことをいう。条件付き確率は P(A|B) または PB(A) のように表される。
Wikipedia
と説明が書いてありますが、正直、よくわかりません ショボ━(´·ω·`)━ン
公式を見てみても、いまいちピンときません。
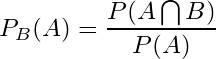
例題を見てみましょう。
4個の赤玉と5個の白玉が入った袋から取り出した玉は袋に戻さずに2回取り出す。1回目に取り出した玉が赤玉であったとき2回目に取り出す玉が白玉である確率を求めなさい。
この問題をみてピンとこない高校生たちは、この問題を先ほどの公式に当てはめようと頑張るのですが、何が P(A∩B) なのか、またどれが P(A) に当たるのかがよく分かりません。
ここでは、ポケモン対戦を例に条件付き確率を学んでいきましょう。
害悪特性「ムラっけ」

オニゴーリやオクタンなどの夢特性である「ムラっけ」は、相手にするととても厄介な特性です。
毎ターン終了時、「こうげき」「ぼうぎょ」「とくこう」「とくぼう」「すばやさ」の中の一つのランクが2段階上がり、別のどれか一つのランクが1段階下がる。
ターンが経過するほど強化されていきます。
これが第7世代までは「かいひりつ」と「めいちゅうりつ」も含まれていて、特に「かいひりつ」が対象に入っていたことがとても厄介なのです。
ポケモンの回避率は1段階上昇するとこちらの技が当たる確率が ×3/4 、2段階上昇すると ×3/5 となります。(こちらの命中に補正がかかっていない場合)
1段階上昇でも命中率100のじしんが命中率70のきあいだまよりも「ちょっとは当たるかなぁ」ぐらいのレベルに落ちるのに、2段階上昇ではきあいだまよりも「当たらねぇ」レベルまで落ちてしまいます。とびひざげりなんて放っていたら膝が割り放題になってしまいますね。(これポケモンやってない人に伝わるのかな)
ちなみに、最大の6段階上昇で ×1/3 になってしまいます。辛い・・・
実際の問題に当てはめて樹形図を書いてみる
例えば、このような対面を考えてみましょう。

この相手のオニゴーリは先ほどのムラっけオニゴーリを仮定します。
1ターン目の行動でギルガルドは「つるぎのまい」で攻撃力を高めました。一方、オニゴーリはムラっけの発動のため「まもる」を選択しました。1ターン目の終了時にオニゴーリはムラっけによりかいひりつを上げてしまいました。この時、2ターン目でギルガルドが命中率90%のせいなるつるぎを当てる確率はいくらでしょうか。ただし、ギルガルドは、2ターン目の攻撃で倒されることはないものとする。
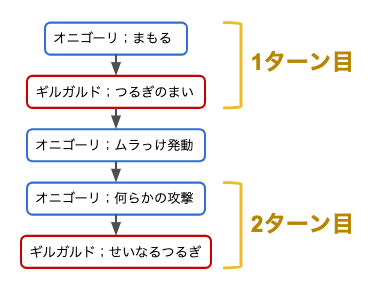
中学生や高校生は確率の問題を解く時に樹形図を書いて考えることが多いと思うので、今回の場合も樹形図に書いていきます。
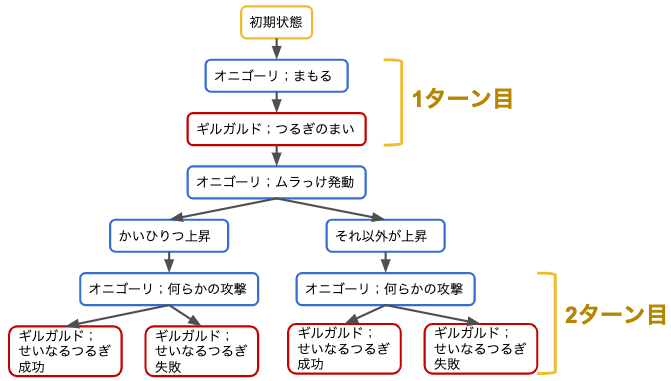
流石にこの図だと長すぎてだるいので、分岐が生じている部分だけ抜き出してみます。
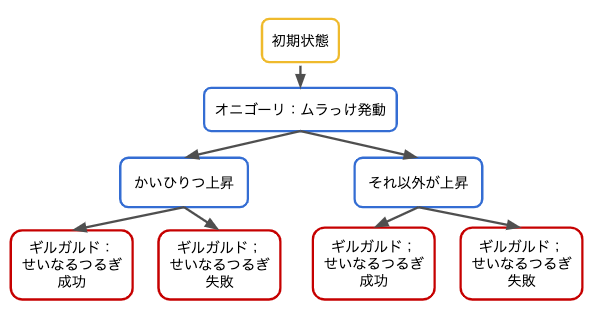
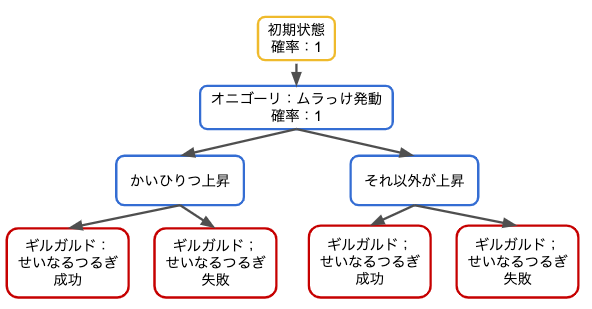
各確率を書き込んでいきましょう。この時、ムラっけが発動するまでは必ず起こる事象なので確率は1になります。
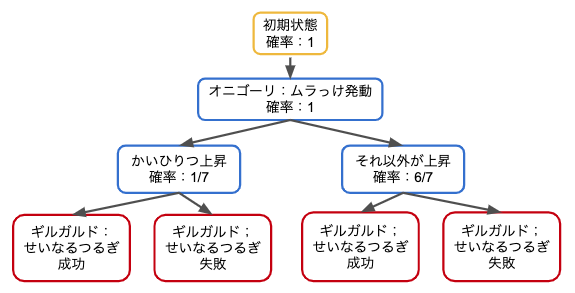
ムラっけによりかいひりつが上がる確率は、他の各ステータスが上がる確率と同様に確からしいはずなので 1/7、それ以外が上がる確率は 6/7 になります。
次は以下の4パターンの確率を求めます。
かいひりつ上昇 → せいなるつるぎ成功
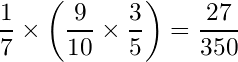
かいひりつ上昇 → せいなるつるぎ失敗
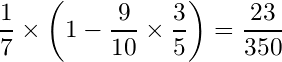
かいひりつ以外のステータスが上昇 → せいなるつるぎ成功
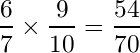
かいひりつ以外のステータスが上昇 → せいなるつるぎ失敗
これで先ほどの樹形図を更新します。
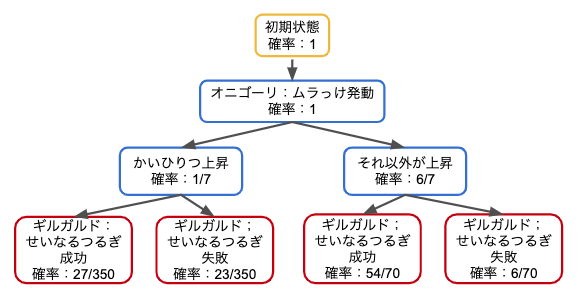
確率を求めてみる
普通の確率
確率は 求めたい部分/全体 で求まります。
例えば、「かいひりつが上がってしまい、かつ、せいなるつるぎが当たる確率」は次のように考えます。
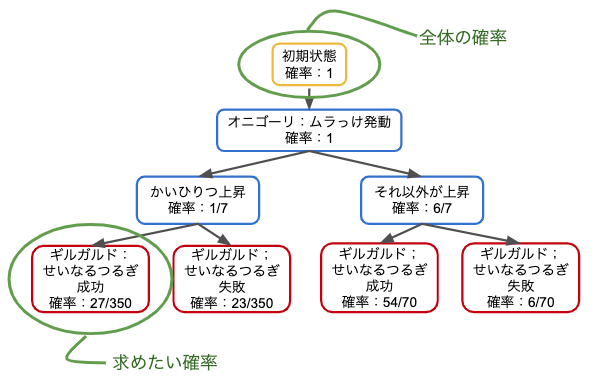
上記の図から、求めたい部分(=分子)は「27/350」です。全体(=分母)はこの樹形図の一番根っこの部分、つまり一番上にある確率「1」にあたります。
なので確率は、
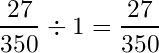
通常はわざわざこんな計算をしなくても良いのですが、これからの流れを分かりやすくするためにあえてしました。
条件付き確率
実は、条件付き確率も同じように求めることができます。先ほどの問題に当てはめてみます。
1ターン目の行動でギルガルドは「つるぎのまい」で攻撃力を高めました。一方、オニゴーリはムラっけの発動のため「まもる」を選択しました。1ターン目の終了時にオニゴーリはムラっけによりかいひりつを上げてしまいました。この時、2ターン目でギルガルドが命中率90%のせいなるつるぎを当てられる確率はいくらでしょうか。ただし、ギルガルドは、2ターン目の攻撃で倒されることはないものとする。
この場合、「オニゴーリがムラっけによりかいひりつを上げた」と言うことはすでに起こってしまった事象なので、そこからの部分に注目して樹形図を見ていきます。
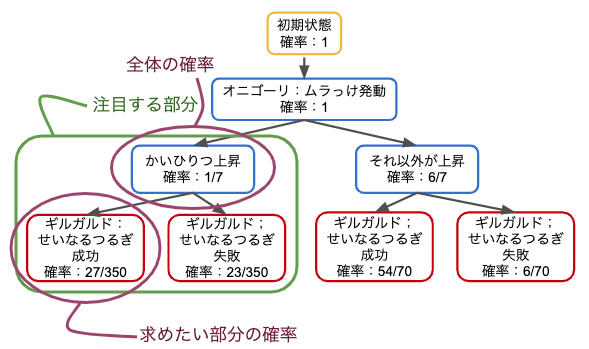
求めたい部分の確率は先ほどと一緒ですが、全体の確率は緑の枠で囲った「注目する部分」の一番上(かいひりつ上昇)にあたります。
よって求める条件付き確率は、
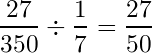
最初の例題にも当てはめてみる
実際のテストとかにはポケモンの事例など出てくるはずもなく、例題のような無機質な問題が出てきます。
4個の赤玉と5個の白玉が入った袋から取り出した玉は袋に戻さずに2回取り出す。1回目に取り出した玉が赤玉であったとき2回目に取り出す玉が白玉である確率を求めなさい。
この問題を先ほどと同様に樹形図に表してみると・・・
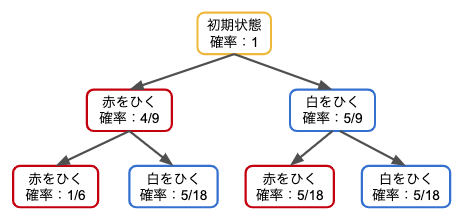
となり、この問題は1回目に赤玉を引くことは確定しているので、1回目に赤玉を引いてからに注目していきます。
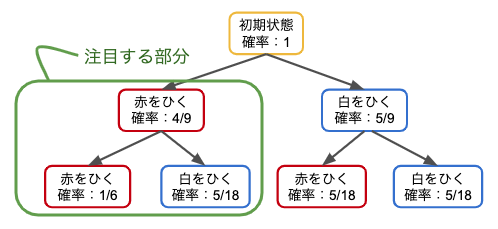
求めたい部分の確率は、1回目が赤玉かつ2回目が白玉なので、5/18
全体の確率は緑の枠の一番上になるので、4/9
よって求めたい条件付き確率は、