やること
「エニグマ」は、第二次世界大戦でナチス・ドイツが用いたローター式暗号機です。

映画「イミテーション・ゲーム」で知ったという方も多いのではないでしょうか。(もう一回見たいなぁ)
ここでは暗号化の最小コードをPythonで実装しながら、最終的にエニグマを作ることを目指します。注意点として、理解を優先するため一部の暗号化アルゴリズムは簡素化しています。より深く正確な情報が知りたい場合は参考文献を当たってみてください。
参考文献
エニグマとは
映画「イミテーション・ゲーム」
暗号理論についてはネットで数多く解説されていますが、こちらのサイトを参考にさせていただきました。
書籍ではこちらがおすすめです。
豆知識
平文を暗号文に変換することを「暗号化」、暗号文を平文に変換することを「復号」と呼びます。「復号化」でも良いらしいですが私の中の誤用警察がスクランブル発進しかけています。日本語もっとがんばれよ・・・!「平文化」はダサいし、それなら「暗号文化」になるし、なんか文化っぽいし・・・
シーザー暗号
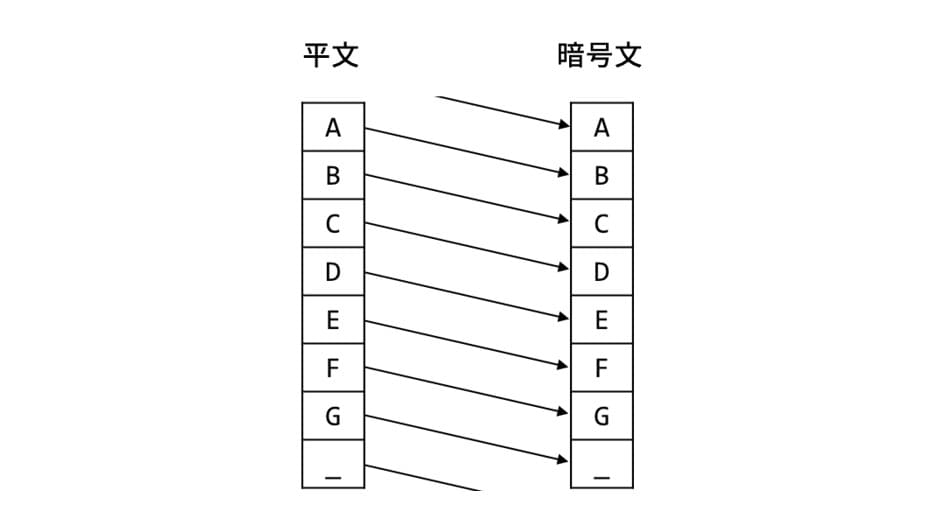
もっとも基本的な暗号の一つ、「シーザー暗号」から実装してみます。平文の各文字をアルファベット順で後ろに何文字かシフトさせるというものです。
ここでは最小コードを書くため、文字は「ABCDEFG_」の8文字のみ用いることにします。”_”はスペースだと思ってください。それでは、1文字後ろにシフトさせるシーザー暗号を書いてみましょう。
'''
シーザー暗号
N文字シフトさせる
'''
#文字テーブル
table = 'ABCDEFG_'
#シフト量
shift = 1
#暗号化関数
def encrypt(word):
#暗号文初期化
ret = ''
for w in word:
#文字→インデックス
index = table.index(w)
#シフト
index = (index + shift) % 8
#シフトした文字
ret += table[index]
return ret
print(encrypt('EGG_CAFE'))F__ADBGF「EGG_CAFE」が「F__ADBGF」に変換されました。アルファベットの後ろ方向に1文字シフトしていますね。平文に2回登場する”G”がどちらも同じ”_”に変換されています。復号は1文字ずつ手前にシフトさせるだけです。
この方法は、十分に長い暗号文が与えられたとき、頻度分析という方法で容易に突破されてしまいます。英語の文章で統計的に多く登場する文字は「e」「t」「a」・・・なので、暗号文でもっとも多くカウントされた文字が「e」に対応している、と分かってしまうのです。
しかし、短い暗号文では信頼のある統計が取れません。暗号文が長ければ長いほど解読されやすいという特性があることを覚えておきましょう。
ヴィジュネル暗号(その1)
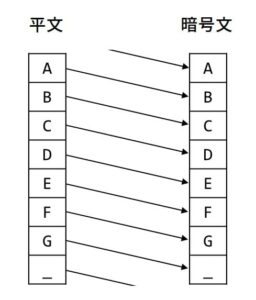
シーザー暗号の弱点を克服した方法が「ヴィジュネル暗号」です。文字毎にシフト量を変えるというものです。
ここでは単純化したヴィジュネル暗号を実装してみます(※本来のアルゴリズムとは違います)。平文の文字を1文字目から順にシフト量 1, 2, 3, 1, 2, 3…とずらしてみます。
'''
ヴィジュネル暗号
シーザー暗号のシフト量を毎回変える
'''
#文字テーブル
table = 'ABCDEFG_'
#シフト量
shift_set = [1, 2, 3]
def encrypt(word):
#暗号文初期化
ret = ''
for i, w in enumerate(word):
#文字→インデックス
index = table.index(w)
#シフト量
shift = shift_set[i % 3]
#シフト
index = (index + shift) % 8
#シフトした文字
ret += table[index]
return ret
print(encrypt('EGG_CAFE'))FABAEDGG「EGG_CAFE」が「FABAEDGG」に変換されました。平文の”GG”は”AB”に変換されていて、シフト量が毎回変わっていることが分かります。復号は [1, 2, 3] というシフト量のセットを知っていれば可能です。
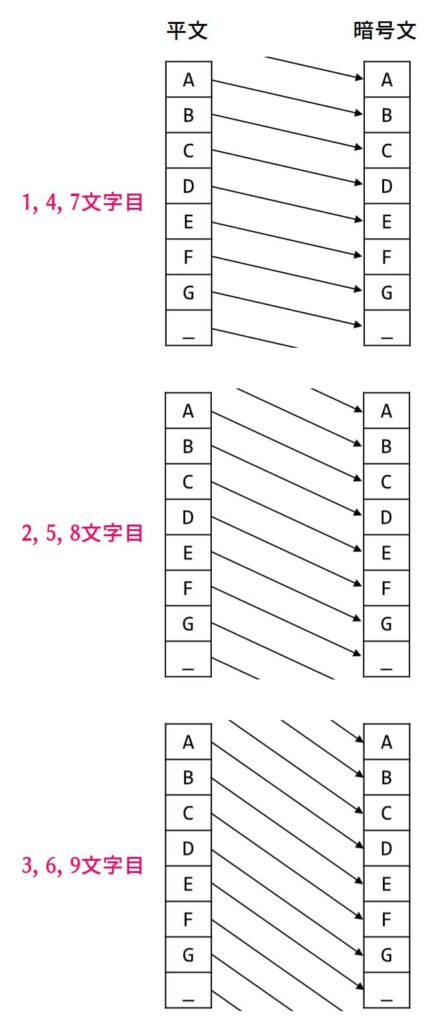
ただ、この方法にも弱点があります。今回のシフト量セットの周期は3なので、3文字毎に同一のシフト量で変換されています。つまり、暗号文を3文字毎に取り出したものはシーザー暗号と変わらず、頻度分析で解けることを意味しています。この作業を3N、3N+1、3N+2のように3セット行えば解けるということです。
実際の解読作業においては何文字毎に取り出せばいいか不明ですが、なんかうまいこと推定できるようです。(説明放棄)
ヴィジュネル暗号(その2)
そろそろエニグマのアルゴリズムに入りたいですが、きちんと理解するため丁寧に寄り道します。ヴィジュネル暗号の弱点を克服するために周期を長くしてみましょう。
とりあえず周期を8にしてみます。
'''
ヴィジュネル暗号2
シフト量周期を8に増やす
'''
#文字テーブル
table = 'ABCDEFG_'
#シフト量
shift_set = [1, 2, 3, 4, 5, 6, 7, 0]
def encrypt(word):
#暗号文初期化
ret = ''
for i, w in enumerate(word):
#文字→インデックス
index = table.index(w)
#シフト量
shift = shift_set[i % 8]
#シフト
index = (index + shift) % 8
#シフトした文字
ret += table[index]
return ret
print(encrypt('EGG_CAFE'))FABD_GEEたかだか周期8では大した防御力になりませんが、例えば1万字の暗号文があったとき、周期3では3333字のシーザー暗号文を頻度分析することになりますが、周期8では1250字のシーザー暗号を対処することになります。
頻度分析は与えられた暗号文が長ければ長いほど解きやすいことを学びました。つまり何が言いたいかというと、ヴィジュネル暗号の周期が長ければ長いほど防御力が高くなるのです。
はい、ここでお笑い芸人Iさんから一言。
平日の昼間からゴロゴロ~ゴロゴロ~
あ~あ、周期が無限大のヴィジュネル暗号があったらなぁ~
おわりに
ということで②エニグマ編に続きます。