AI要約
HOBO対応の疑似アニーリングパッケージ「HOBOTAN」を用い、ペンシルパズル「ビルディングパズル」を解く挑戦を記録。量子アニーリングの特性を活用し、複雑な制約の解法に迫ります。高度な知識が求められる試みで、解法プロセスとその結果を詳しく解説します。
やること
まだまだ行きます。HOBO対応の疑似アニーリングパッケージ「HOBOTAN」でペンシルパズルを解くシリーズ。
今回は「ビルディングパズル(Skyscrapers)」を解いてみましょう。非常に難しかったです。
事前知識
この記事はTYTAN(QUBOアニーリング)の基礎講座を履修済みであることを前提としています。詳しくはHOBOTANの記事をご参照ください。
HOBOTAN本体のGithubはこちらです。使い方はTYTANとほとんど同じです。分からないことがあれば何でも聞いてください。
ビルディングパズル(Skyscrapers)とは
またまた Puzzle Team さんから問題を拝借しました。いつもありがとうございます。
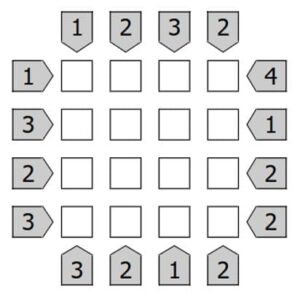
16個のマスを1~4の数字で埋めます。どの行も列も数字が重複してはいけません。マスに書き込む数字はビルの高さを表していて、ある方向から見たときにいくつのビルが見えるかが指定されています。例えば手前から順に3,2,4,1と書き込んだ場合、3,4のビルは見えますが2,1のビルは隠れて見えません。この場合は2棟が見えることになります。
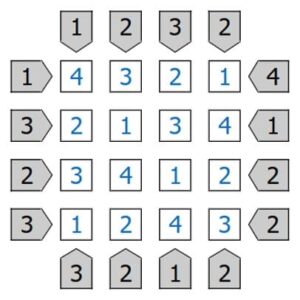
答えはこちらです。
コンセプティスパズル さんでも遊べます。
定式化と予備実験
長らくQUBOで定式化できず困っていました。まぢムリ。。2次制約で収まる方法があるのでしょうか?もうね、諦めてHOBOで取り組むことにしました。
まずは簡略化して4つのビルを考えてみます。4×4の量子ビットを用意して次のように対応させます。
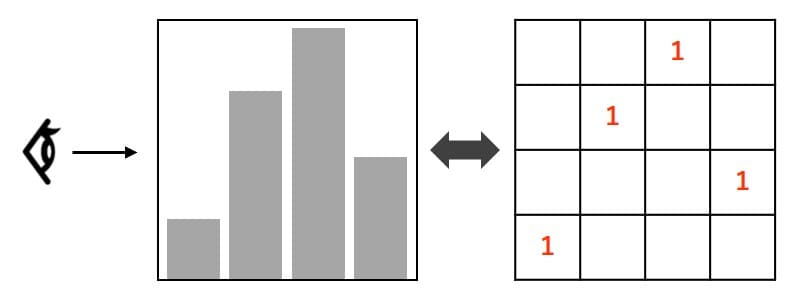
まず、一番手前の列(1列目)のビルが必ず見えるのは自明ですね。
問題は2列目以降です。2列目は次のように考えました。簡単に言うと「自分の前にあるビルが自分より低ければ見えるよね」です。もし「自分の高さが4」かつ「1列目のビルの高さが1~3」であれば見えます。または、「自分の高さが3」かつ「1列目のビルの高さが1~2」でも見えます。または、「自分の高さが2」かつ「1列目のビルの高さが1」でも見えます。この3パターンの”見える”を合計したものが、2列目のビルが見えるかどうかの判定(0or1)となります。
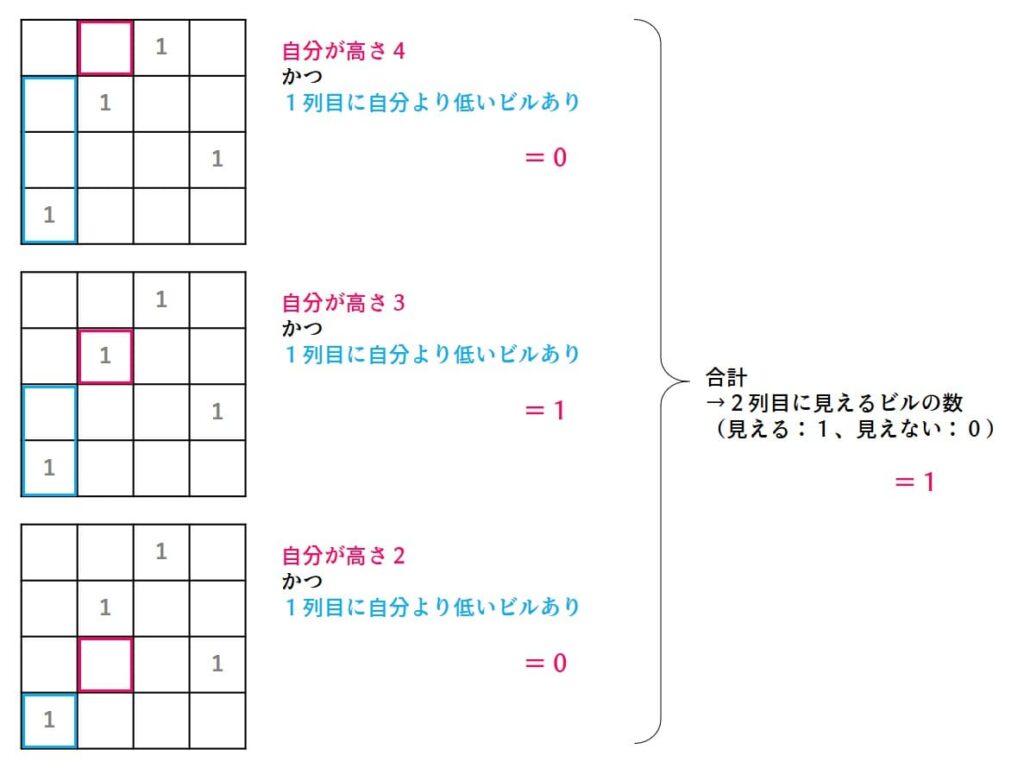
4列目についても考えてみましょう。発想は同じで、「自分の前にあるすべてのビルが自分より低ければ見えるよね」です。判定条件が長くなります。もし「自分の高さが4」かつ「1列目のビルの高さが1~3」かつ「2列目のビルの高さが1~3」かつ「3列目のビルの高さが1~3」であれば見えます。以下同文。
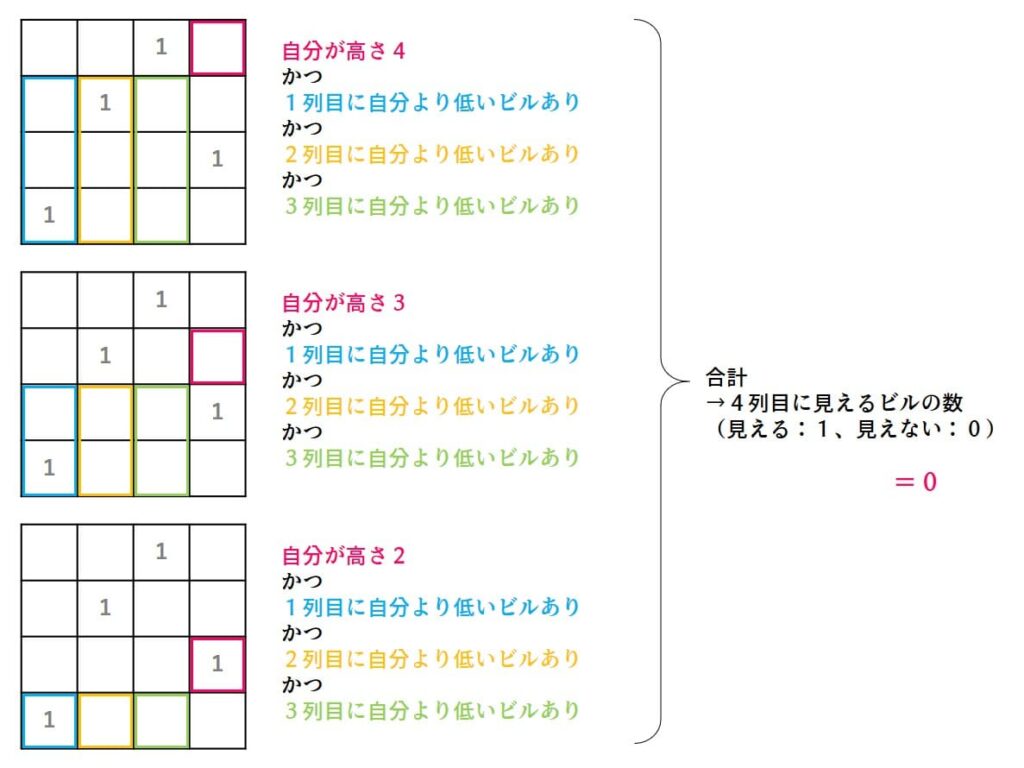
定式化において「かつ」はかけ算でした。4列目は「A かつ B かつ C かつ D」が登場するので4次の制約になります。(実際にはさらに2乗するので8次になる)
ということで実装してみます。解は理想的なエネルギーのだけ表示するようにしています。
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットの用意
q = symbols_list([4, 4], 'q{}_{}')
#式を用意
H = 0
#各行に1個、各列に1個
for i in range(4):
H += (np.sum(q[i, :]) - 1)**2
for j in range(4):
H += (np.sum(q[:, j]) - 1)**2
#手前から1番目のビルが見えるかどうか(見える:1、見えない:0)
num0 = 1
#手前から2番目のビルが見えるかどうか
num1 = 0
num1 += q[0, 1] * np.sum(q[1:, 0])
num1 += q[1, 1] * np.sum(q[2:, 0])
num1 += q[2, 1] * np.sum(q[3:, 0])
#手前から3番目のビルが見えるかどうか
num2 = 0
num2 += q[0, 2] * np.sum(q[1:, 0]) * np.sum(q[1:, 1])
num2 += q[1, 2] * np.sum(q[2:, 0]) * np.sum(q[2:, 1])
num2 += q[2, 2] * np.sum(q[3:, 0]) * np.sum(q[3:, 1])
#手前から4番目のビルが見えるかどうか
num3 = 0
num3 += q[0, 3] * np.sum(q[1:, 0]) * np.sum(q[1:, 1]) * np.sum(q[1:, 2])
num3 += q[1, 3] * np.sum(q[2:, 0]) * np.sum(q[2:, 1]) * np.sum(q[2:, 2])
num3 += q[2, 3] * np.sum(q[3:, 0]) * np.sum(q[3:, 1]) * np.sum(q[3:, 2])
#見えるビルの数
H += (num0 + num1 + num2 + num3 - 4)**2
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=100)
#理想的な解のみ
for r in result:
print(f'Energy {r[1]}, Occurrence {r[2]}')
if (r[1] + offset)**2 < 0.1:
#配列取得
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}')
#さくっと画像に
img, subs = Auto_array(r[0]).get_image('q{}_{}')
plt.figure(figsize=(3, 3))
plt.imshow(img)
plt.show()tensor order = 8
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
17.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 100/2000 min=-15.0 mean=2.819999933242798
.......... 200/2000 min=-16.0 mean=2.069999933242798
.......... 300/2000 min=-16.0 mean=14.469999313354492
(中略)
.......... 1800/2000 min=-17.0 mean=14.579999923706055
.......... 1900/2000 min=-17.0 mean=13.639999389648438
.......... 2000/2000 min=-17.0 mean=13.269999504089355
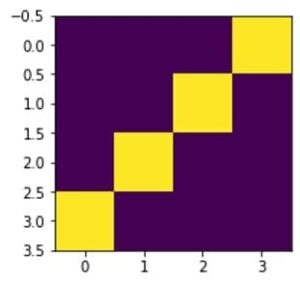
Energy -17.0, Occurrence 15やはり8次の式になったようです。「4棟見える」にしたので以下の1パターンが出ました。4棟見えるのはこのパターンしかないですね。
「3棟見える」だと以下の6通りが出ました。

「2棟見える」だと以下の11通り。
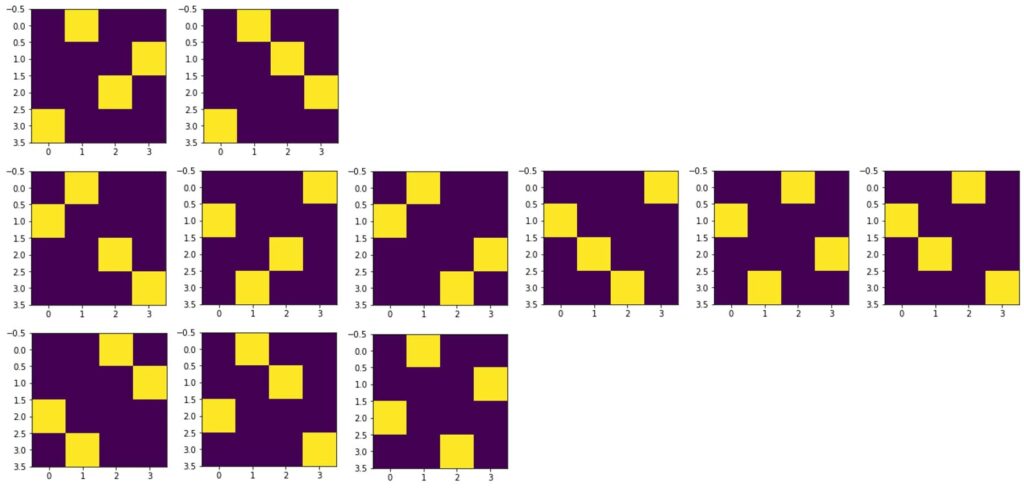
「1棟見える」は以下の6通り。

網羅できていると思います。全部で4!=24通り。この予備実験の段階で必要十分な解が出ていることを入念に確認しておく必要があります。「エネルギーは理想的なのに間違った解が出る」とか「正しい解なのにエネルギーが理想にならない」ということがあってはいけません。そのまま先に進んでも永久にパズルは解けません。
パズルへの拡張
問題を再掲。

まず、数独と同じように4x4x4の量子ビットを用意しましょう(→量子アニーリング(QUBO)でナンプレ(数独)と不等号ナンプレを解く)。
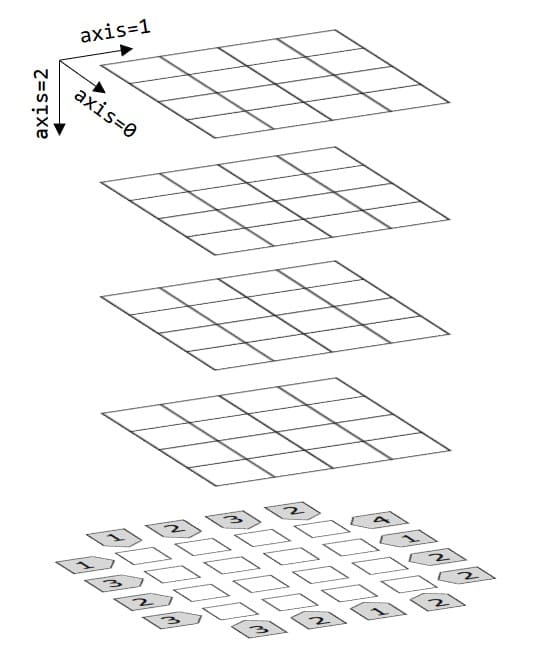
数独と同じように「どの直線の4個もワンホット」にします。これの意味は、「ある行には高さNのビルが必ず一つ」とか「ある列には高さNのビルが必ず一つ」とか「あるマスに立つビルは必ず一つ」みたいなことです。
あとは周囲から見えるビルの数を設定していくのですが、予備実験のやつを関数化して、3次元配列から切り出した2次元配列を渡してやることにします。切り出す方向が難しいですね。うお~~(paizaで鍛えたPython力がうなりを上げる)
from hobotan import *
import numpy as np
import matplotlib.pyplot as plt
#量子ビットの用意
q = symbols_list([4, 4, 4], 'q{}_{}_{}')
#式を用意
H = 0
#各次元に超絶ワンホット
for i in range(4):
for j in range(4):
H += (np.sum(q[i, j, :]) - 1)**2
for i in range(4):
for k in range(4):
H += (np.sum(q[i, :, k]) - 1)**2
for j in range(4):
for k in range(4):
H += (np.sum(q[:, j, k]) - 1)**2
def visible_num(s):
'''
4x4の量子ビット配列を入力
見える数 num0 + num1 + num2 + num3 を返す
'''
#手前から1番目のビルが見えるかどうか(見える:1、見えない:0)
num0 = 1
#手前から2番目のビルが見えるかどうか
num1 = 0
num1 += s[0, 1] * np.sum(s[1:, 0])
num1 += s[1, 1] * np.sum(s[2:, 0])
num1 += s[2, 1] * np.sum(s[3:, 0])
#手前から3番目のビルが見えるかどうか
num2 = 0
num2 += s[0, 2] * np.sum(s[1:, 0]) * np.sum(s[1:, 1])
num2 += s[1, 2] * np.sum(s[2:, 0]) * np.sum(s[2:, 1])
num2 += s[2, 2] * np.sum(s[3:, 0]) * np.sum(s[3:, 1])
#手前から4番目のビルが見えるかどうか
num3 = 0
num3 += s[0, 3] * np.sum(s[1:, 0]) * np.sum(s[1:, 1]) * np.sum(s[1:, 2])
num3 += s[1, 3] * np.sum(s[2:, 0]) * np.sum(s[2:, 1]) * np.sum(s[2:, 2])
num3 += s[2, 3] * np.sum(s[3:, 0]) * np.sum(s[3:, 1]) * np.sum(s[3:, 2])
return num0 + num1 + num2 + num3
#問題の反映
#左から見る
aim = [1, 3, 2, 3]
for i in range(4):
q_tmp = q[i, :, :].T
H += (visible_num(q_tmp) - aim[i])**2
#右から見る
aim = [4, 1, 2, 2]
for i in range(4):
q_tmp = q[i, :, :].T[:, ::-1]
H += (visible_num(q_tmp) - aim[i])**2
#上から見る
aim = [1, 2, 3, 2]
for j in range(4):
q_tmp = q[:, j, :].T
H += (visible_num(q_tmp) - aim[j])**2
#下から見る
aim = [3, 2, 1, 2]
for j in range(4):
q_tmp = q[:, j, :].T[:, ::-1]
H += (visible_num(q_tmp) - aim[j])**2
#HOBOテンソルにコンパイル
hobo, offset = Compile(H).get_hobo()
print(f'offset\n{offset}')
#サンプラー選択
solver = sampler.MIKASAmpler()
#サンプリング
result = solver.run(hobo, shots=200, T_num=10000)
#上位3件
for r in result[:3]:
print(f'Energy {r[1]}, Occurrence {r[2]}')
#配列取得
arr, subs = Auto_array(r[0]).get_ndarray('q{}_{}_{}')
#ワンホットチェック
check = np.sum(arr, axis=2)
print(f'check\n{check}')
#解答
ans = 4 - np.argmax(arr, axis=2)
print(f'ans\n{ans}')tensor order = 8
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
80.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 200/10000 min=-24.0 mean=62.26499938964844
.......... 400/10000 min=-25.0 mean=72.12999725341797
.......... 600/10000 min=-28.0 mean=66.61000061035156
(中略)
.......... 9600/10000 min=-80.0 mean=204.5349884033203
.......... 9800/10000 min=-80.0 mean=182.93499755859375
.......... 10000/10000 min=-80.0 mean=162.47999572753906
Energy -80.0, Occurrence 2
check
[[1 1 1 1]
[1 1 1 1]
[1 1 1 1]
[1 1 1 1]]
ans
[[4 3 2 1]
[2 1 3 4]
[3 4 1 2]
[1 2 4 3]]
Energy -77.0, Occurrence 1
check
[[1 1 1 1]
[1 1 1 1]
[1 1 1 1]
[1 1 1 1]]
ans
[[4 3 2 1]
[3 2 1 4]
[1 4 3 2]
[2 1 4 3]]
Energy -76.0, Occurrence 1
check
[[1 1 1 1]
[1 1 1 1]
[1 1 1 1]
[1 1 1 1]]
ans
[[4 3 2 1]
[2 1 3 4]
[3 4 1 2]
[1 3 4 2]]上位3件の解を表示しています。チェックとして各マスのビルが一つだけになっているかどうかを確認しつつ、答えの数字に戻しています。
#1番目の解
[[4 3 2 1]
[2 1 3 4]
[3 4 1 2]
[1 2 4 3]]
一致していますね。お見事!
もう一問
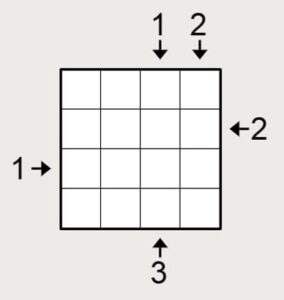
コンセプティスパズル さんの問題も解いてみましょう。
tensor order = 8
----- compile -----
MODE: GPU
DEVICE: cuda:0
-------------------
offset
54.0
===== sampler =====
MODE: GPU
DEVICE: cuda:0
===================
.......... 200/20000 min=-28.0 mean=17.98499870300293
.......... 400/20000 min=-28.0 mean=25.154998779296875
.......... 600/20000 min=-28.0 mean=27.93000030517578
(中略)
.......... 19600/20000 min=-54.0 mean=36.70000076293945
.......... 19800/20000 min=-54.0 mean=30.65999984741211
.......... 20000/20000 min=-54.0 mean=30.049999237060547
Energy -54.0, Occurrence 2
check
[[1 1 1 1]
[1 1 1 1]
[1 1 1 1]
[1 1 1 1]]
ans
[[2 1 4 3]
[3 4 1 2]
[4 2 3 1]
[1 3 2 4]]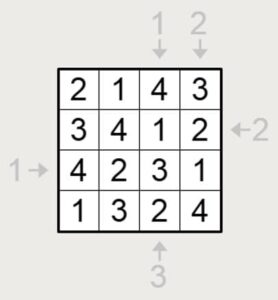
きちんと理想エネルギーで出ました。こんなに少ない指定で一意に定まるんですね。奥が深い!
おわりに
問題が4×4サイズなので8次制約。6×6サイズもあるようなので12次制約に。。うーん、考えないことにします シラニコ ʅ ( ˘ω˘ ) ʃ シラゴネッティ