実行環境
Windowsマシンで実行する方にはWinPython3.6をおすすめしています。インストール不要で、USBメモリに入れて持ち運ぶこともできます。
WinPython3.6をおすすめしています。
オンライン実行環境のGoogle Colaboratoryもおすすめです。
Google Colaboratoryが利用可能です。

MacやLinuxの方は頑張ってください。
vcoptのインストール
ターミナル(WinPythonの場合は「WinPython Command Prompt.exe」)で以下を実行すると、最新バージョンがインストールされます。
pip install vcopt古いバージョンをアップデートする場合はこちらです。
pip install -U vcoptColabの場合は、先頭に!マークを付けることでシェルスクリプトとして実行されます。
!pip install vcoptNo.1|二次関数の最小値
問題
二次関数 y=x^2 の最小値を求めてみましょう。x を (-5 < x < 5) の範囲であちこち動かして、y が最小になるときの x を探します。
考え方
実数値の最適化ですから、vcopt().rcGA()を使います。
パラメータは x ひとつで、パラメータ範囲は [最小値, 最大値] = [-5, 5] です。評価関数は二次関数、すなわち x を受け取って x^2 を返す関数です。また、評価関数の目標値はよくわからないので -9999 とします(実際の最小値は0ですが、それが分かっていたら苦労しませんので、知らないこととします)。
次のように書きます。
from vcopt import vcopt
#評価関数(二次関数)
def niji_kansu(para):
y = para**2
return y
#パラメータ範囲
para_range = [-5, 5]
print(para_range)
#GAで最適化
para, score = vcopt().rcGA(para_range, #パラメータ範囲
niji_kansu, #評価関数
-9999) #目標値
#結果の表示
print(para)
print(score)結果
[-5, 5]
________________________________________ info ________________________________________
para_range : n=1
score_func : <class 'function'>
aim : ==-9999.0
show_pool_func : 'bar'
seed : None
pool_num : 10
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 10/10
| +< | gen=50, best_score=0.0003
_______________________________________ result _______________________________________
para = np.array([0.08992197958749593])
score = 0.008085962412934035
________________________________________ end _________________________________________
[0.08992198]
0.008085962412934035このような結果が表示されます。内部の乱数により、厳密に上記と同じ結果にはなりません。
info欄にはGAの設定値が表示されますが、特に指定しない限り、適当な値が自動的に設定されます。start欄には最適化の進捗バーが表示されますが、一瞬で終わったため見えなかったと思います。result欄には最適なパラメータと評価値が表示されます。上記の例では、x=-0.090, y=0.0081 となりました。
え?x=0.0, y=0.0 じゃないの?
GAはメタヒューリスティックな最適化手法のひとつで、大雑把に言えば「いろいろな問題に対応できるが、ざっくりとした解しか得られない手法」です。厳密に x=0.0, y=0.0 を求めようとすると極端に時間がかかるため、vcopt では大雑把な解で停止するようにしています。より厳密な解を得たい場合は、この後にさらに最急降下法などを行うことを検討してください。
No.2|5次元のRastrigin関数の最小値
問題
5次元のRastrigin関数の最小値を求めます。この関数はとてもギザギザした解空間をもつ関数で、最適値は5つの x がすべて0のときですが、x=-1 や x=1 のところにも深い谷があり、そちらに足を取られると x=0 が見つかりません。x の範囲は (-5.12 < x < 5.12) とします。

考え方
これも実数値の最適化ですから、vcopt().rcGA()を使います。
パラメータは5つで、ひとつのパラメータ範囲は [最小値, 最大値] = [-5.12, 5.12] です。パラメータは5つあるため、これを5つ並べた2次元配列 [[-5.12, 5.12], [-5.12, 5.12], [-5.12, 5.12], [-5.12, 5.12], [-5.12, 5.12]] を用意します。評価関数はRastrigin関数で、5つのパラメータが入った配列 [x0, x1, x2, x3, x4] を受け取って計算値を返します。また、評価関数の目標値はよくわからないので -9999 とします(実際の最小値は0ですが、それが分かっていたら苦労しませんので、知らないこととします)。
次のように書きます。今回は最適化の途中経過を show_pool_func=’print’ オプションで見てみます(デフォルトは ‘bar’ )。
import math
from vcopt import vcopt
#評価関数(Rastrigin関数)
def rastrigin_kansu(para):
k = 0
for x in para:
k += 10 + (x*x - 10 * math.cos(2*math.pi*x))
return k
#パラメータ範囲
para_range = [[-5.12, 5.12] for _ in range(5)]
print(para_range)
#GAで最適化
para, score = vcopt().rcGA(para_range, #パラメータ範囲
rastrigin_kansu, #評価関数
-9999, #目標値
show_pool_func='print') #表示オプション
#結果の表示
print(para)
print(score)結果
[[-5.12, 5.12], [-5.12, 5.12], [-5.12, 5.12], [-5.12, 5.12], [-5.12, 5.12]]
________________________________________ info ________________________________________
para_range : n=5
score_func : <class 'function'>
aim : ==-9999.0
show_pool_func : 'print'
seed : None
pool_num : 50
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 50/50
gen= 0, best_score= 102.205, mean_score= 128.469, mean_gap=10127.469, time= 0.3
gen= 50, best_score= 59.091, mean_score= 102.306, mean_gap=10101.306, time= 0.3
gen= 100, best_score= 56.028, mean_score= 84.216, mean_gap=10083.216, time= 0.3
gen= 150, best_score= 49.991, mean_score= 71.447, mean_gap=10070.447, time= 0.3
.
.
.
gen= 7250, best_score= 0.000, mean_score= 0.638, mean_gap=9999.638, time= 1.4
gen= 7300, best_score= 0.000, mean_score= 0.638, mean_gap=9999.638, time= 1.4
gen= 7350, best_score= 0.000, mean_score= 0.555, mean_gap=9999.555, time= 1.4
gen= 7400, best_score= 0.000, mean_score= 0.551, mean_gap=9999.551, time= 1.4
_______________________________________ result _______________________________________
para = np.array([4.350281024301239e-09, 1.9701076325873146e-08, 1.6530518287538598e-08, 2.856045977495114e-08, -3.7097419358644856e-08])
score = 5.702105454474804e-13
________________________________________ end _________________________________________
[ 4.35028102e-09 1.97010763e-08 1.65305183e-08 2.85604598e-08
-3.70974194e-08]
5.702105454474804e-13内部の乱数により、厳密に上記と同じ結果にはなりません。
result欄に、最適なパラメータ5つとRastrigin関数の評価値が表示されています。パラメータは5つとも0、評価値も0になりましたでしょうか?
他のオプションも使ってみたい!
他によく使うオプションは show_pool_func=’plot’、seed、pool_num です。また、目標値には比較演算子を使った文字列も使えますので、「評価値が1.0を下回ったら止めていいや」ということもできます。該当部分を次のように書き換えて実行してみます。
#GAで最適化
para, score = vcopt().rcGA(para_range, #パラメータ範囲
rastrigin_kansu, #評価関数
'<1.0', #目標値
show_pool_func='plot', #表示オプション
seed=0, #乱数シード
pool_num=100) #個体数show_pool_func=’plot’ はGA中の個体群の評価値をグラフで可視化してくれます。seed=0 のように乱数シードを指定すると、何度実行しても同じ結果になりますので、再現性が保証されます。pool_num=100 は個体数を100に変更します。デフォルトはパラメータ数の10倍ですが、よりしっかりと探索したい場合はこれを増やすことをおすすめします。一方で、あまりにも実行が遅い場合は、この数を減らすことで、探索力を犠牲にして高速化することもできます。
No.3|お釣りの金額
問題
999円までの買い物であれば、財布に500円玉・50円玉・5円玉が各1枚、100円玉・10円玉・1円玉が各4枚あれば、どんな金額でもピッタリ支払えるはずです。お会計が594円のとき、小銭をどのような組み合わせで出せばよいでしょうか。
ちなみに594円は、540円(8%税込)を消費税の増税に便乗して540円(税抜)とした場合の支払い金額です。
考え方
離散的な組合せ最適化ですから、vcopt().dcGA()を使います。
パラメータは各小銭に対応させて6つとします。パラメータ範囲はそれぞれの選択肢を並べた2次元配列 [[0, 500], [0, 100, 200, 300, 400], [0, 50], [0, 10, 20, 30, 40], [0, 5], [0, 1, 2, 3, 4]] とします。評価関数では小銭を合計して594円との差を返します。また、評価関数の目標値は0です。
次のように書きます。
from vcopt import vcopt
#評価関数(金額を合計し、594円との差を返す)
def otsuri(para):
money = sum(para)
return abs(594 - money)
#パラメータ範囲(選択肢を並べた2次元配列)
para_range = [[0, 500],
[0, 100, 200, 300, 400],
[0, 50],
[0, 10, 20, 30, 40],
[0, 5],
[0, 1, 2, 3, 4]]
#GAで最適化
para, score = vcopt().dcGA(para_range, #パラメータ範囲
otsuri, #評価関数
0) #目標値
#結果の表示
print(para)
print(score)結果
________________________________________ info ________________________________________
para_range : n=6
score_func : <class 'function'>
aim : ==0.0
show_pool_func : 'bar'
seed : None
pool_num : 60
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 60/60
|+ < | gen=660, best_score=0.0
_______________________________________ result _______________________________________
para = np.array([500, 0, 50, 40, 0, 4])
score = 0.0
________________________________________ end _________________________________________
[500 0 50 40 0 4]
0.0内部の乱数により、厳密に上記と同じ結果にはなりません。
結果、500円玉、50円玉、10円玉×4枚、1円玉×4枚でピッタリ支払えることがわかりました。
No.4|10ヶ所の街を最短で訪れる経路
問題
10ヶ所の街を最短で訪れるための順序と総距離を求めます。街の座標は (0 < x < 1), (0 < y < 1) の範囲のランダムな10点です。
街の座標は次のように作成します。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcopt
#街の座標の作成
nr.seed(0)
town_x = nr.rand(10)
town_y = nr.rand(10)
#街のプロット
plt.plot(town_x, town_y, 'ok')
plt.xlabel('x'); plt.ylabel('y')
plt.show()
考え方
順序(並び替え)は、vcopt().opt2() で局所最適化、vcopt().tspGA() で大域最適化が行えます。
vcopt().opt2() は、適当な順序配列(例えば [3, 2, 6, 1, 0, 9, 4, 7, 5, 8])から始めて逐次的に改善していきます。評価関数として、順序配列を受け取り、街の座標を使って総距離を計算して返す関数も用意します。評価関数の目標値はよくわからないので0とします(もちろん0にはなりませんが)。
局所最適化
評価関数と vcopt().opt2() を次のように書きます。
#評価関数(パラメータ順に回ったときの総距離)
def tsp_score(para):
return np.sum(((town_x[para][:-1] - town_x[para][1:])**2 + (town_y[para][:-1] - town_y[para][1:])**2)**0.5)
#適当な順番を作成
para = range(10)
#2-opt法で最適化
para, score = vcopt().opt2(para, #並び替えたいパラメータ
tsp_score, #評価関数
0.0) #目標値
#結果
print(para)
print(score)
#結果のプロット
plt.plot(town_x[para], town_y[para], 'ok-')
plt.xlabel('x'); plt.ylabel('y')
plt.show()結果
[8 7 0 3 9 2 1 5 6 4]
1.9511600573861472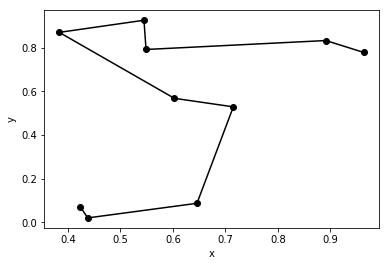
内部の乱数により、厳密に上記と同じ結果にはなりません。
[8 7 0 3 9 2 1 5 6 4] の順に訪れることで、総距離1.95になりました。
大域最適化
vcopt().tspGA() は次のように書きます。
#パラメータ範囲
para_range = range(10)
#GAで最適化
para, score = vcopt().tspGA(para_range, #並び替えたいパラメータ
tsp_score, #評価関数
0.0) #目標値
#結果のプロット
plt.plot(town_x[para], town_y[para], 'ok-')
plt.show()結果
________________________________________ info ________________________________________
para_range : n=10
score_func : <class 'function'>
aim : ==0.0
show_pool_func : 'bar'
seed : None
pool_num : 100
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 100/100
Mini 2-opting first gen 100/100
| + < | gen=1900, best_score=1.8708
_______________________________________ result _______________________________________
para = np.array([4, 6, 5, 1, 2, 0, 9, 3, 7, 8])
score = 1.870825859094424
________________________________________ end _________________________________________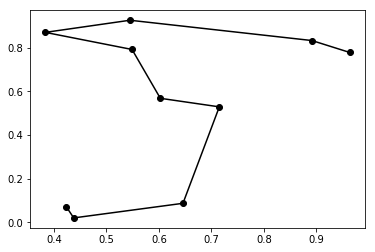
こちらも内部の乱数により、厳密に上記と同じ結果にはなりません。
[4 6 5 1 2 0 9 3 7 8] の順に訪れることで、総距離が1.87まで短くなりました。
もっと問題を試してみたい
仕様書はこちらです。
vcoptを使った記事はこちらです。




