16-21. Pythonのaxisを図で理解する

やること
実行環境
配列の用意
基本編
応用編
まとめ

やること

Python の numpy（○なむぱい、×なんぴー）は優秀な数値計算モジュールであり、配列の合計値を求める際は for文で要素を１つ１つ処理するよりも np.sum() のメソッドで処理したほうが良いです。

np.sum() の他にも、

np.mean(), np.average()　平均値
np.median()　中央値
np.max()　最大値
np.min()　最小値
np.std()　標準偏差
np.var()　分散

があります。

さて、いずれも多次元配列においてどの軸で処理するかという「axis=」のオプションがありますが、「axis=1ってどの方向だっけ？」と迷う方もいると思います。今回は axis をマスターしたいと思います。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

Google Colaboratoryが利用可能です。

Google Colab

配列の用意

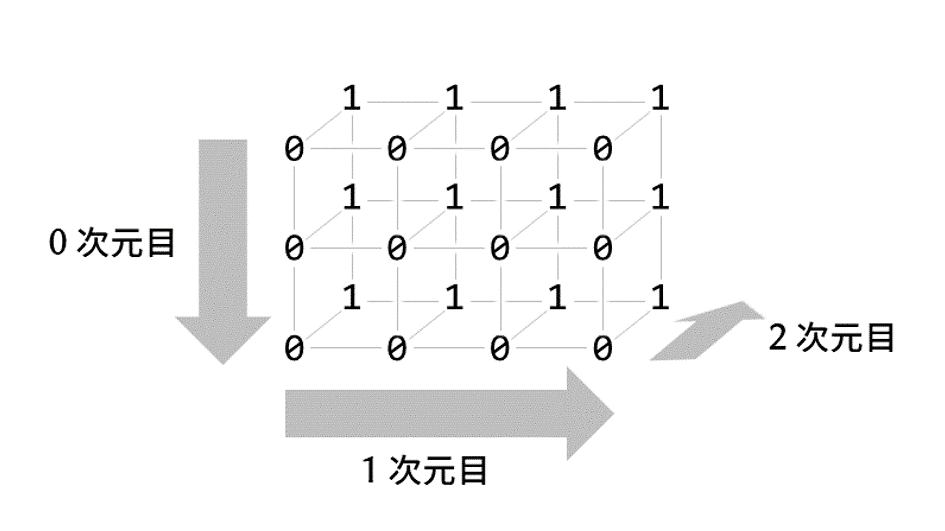
適当な３次元配列を用意しました。

import numpy as np

a = np.array([[[0, 1], [0, 1], [0, 1], [0, 1]],
              [[0, 1], [0, 1], [0, 1], [0, 1]],
              [[0, 1], [0, 1], [0, 1], [0, 1]]])

次のようなイメージです。

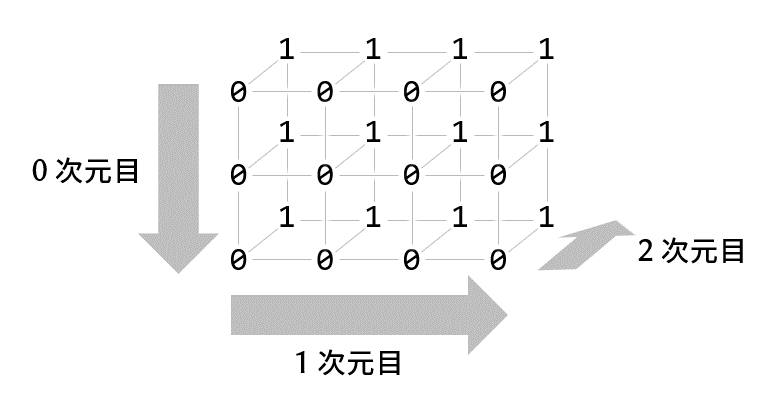
基本編

axisなし

axis が指定されない場合は全要素の和が返ります。

print(np.sum(a))

axis=0

print(np.sum(a, axis=0))

[[0 3]
 [0 3]
 [0 3]
 [0 3]]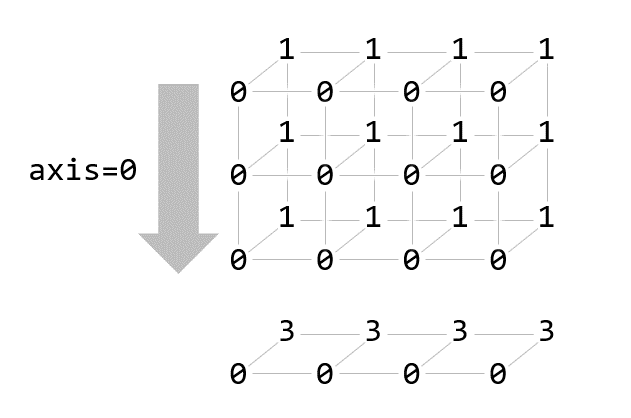

axis=1

print(np.sum(a, axis=1))

[[0 4]
 [0 4]
 [0 4]]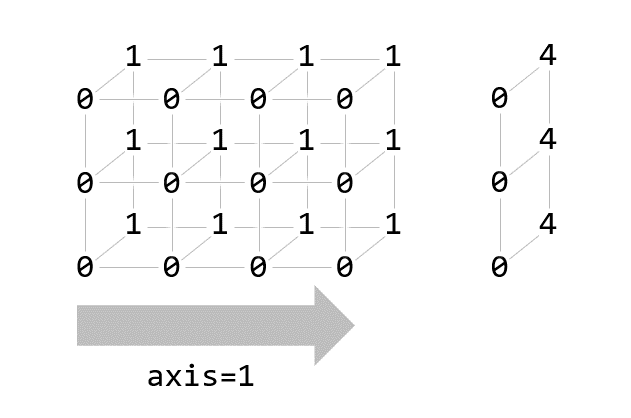

axis=2

print(np.sum(a, axis=2))

[[1 1 1 1]
 [1 1 1 1]
 [1 1 1 1]]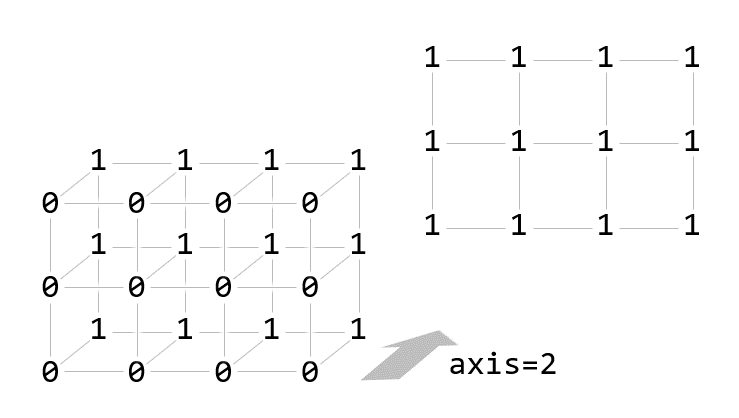

応用編

実は axis=(0, 1) のように複数軸を指定することもできます。

axis=(0, 1)

print(np.sum(a, axis=(0, 1)))

[ 0 12]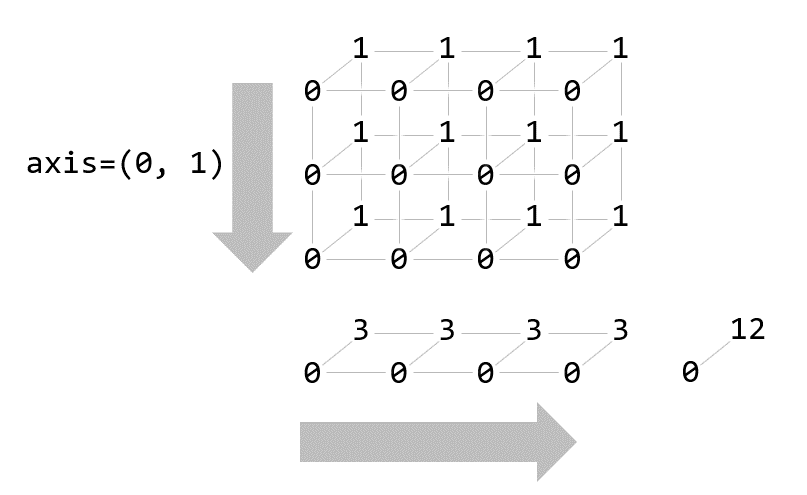

axis=(0, 2)

print(np.sum(a, axis=(0, 2)))

[3 3 3 3]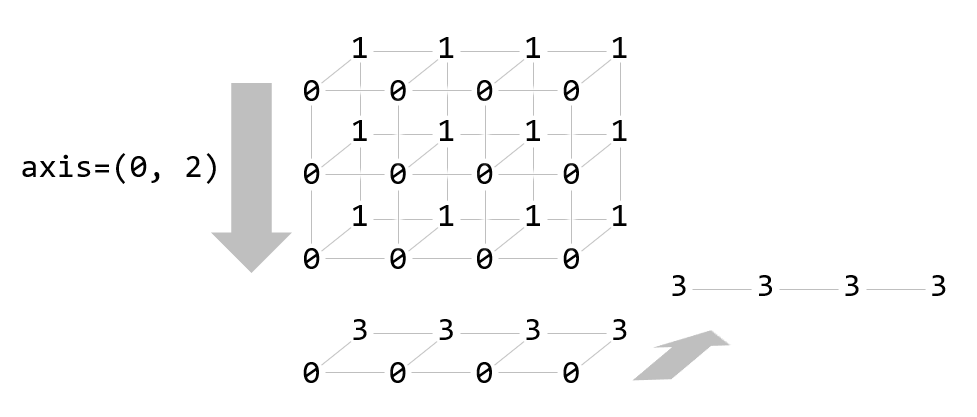

axis=(1, 2)

print(np.sum(a, axis=(1, 2)))

[4 4 4]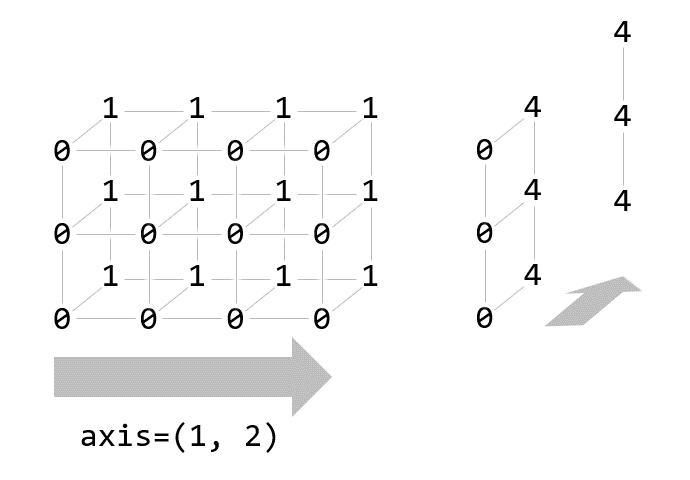

まとめ

これらの図がイメージできれば迷うことはないでしょう！