やること
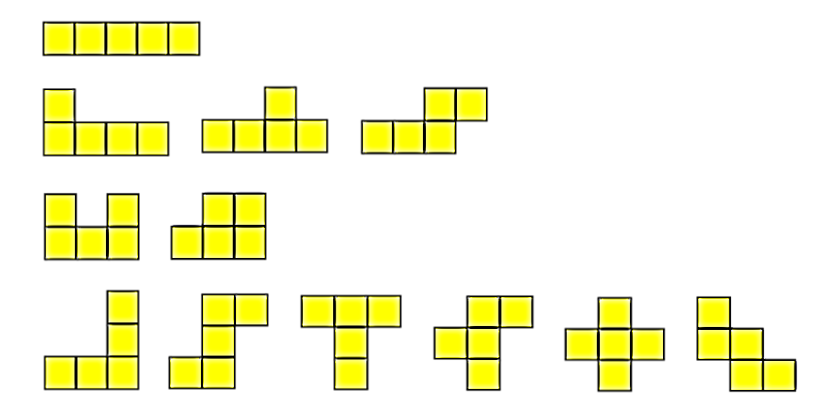
ペントミノと呼ばれる、12種のピースを長方形の枠内に敷き詰めるパズルがあります。
ペントミノ - Wikipedia
これらのピースを
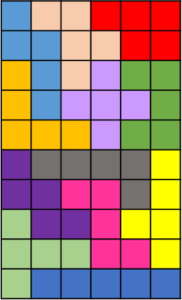
6×10の枠内に敷き詰める場合、次のような解が2339通りあるそうです(マジで!?)。
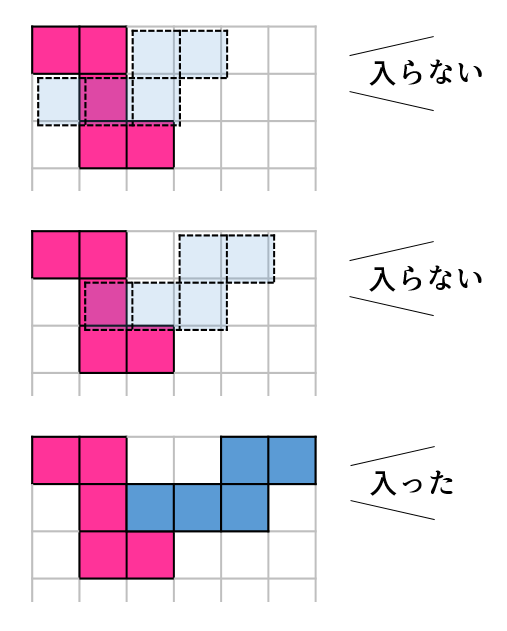
今日は、順序の局所最適化ができるvcopt().opt2()と大域最適化ができるvcopt().tspGA()を用いて、いちばん単純な敷き詰めに挑戦してみます。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
敷き詰めるアルゴリズム:Bottom-Left法
Bottom-Left法は、「左上から詰めて入れる」という感じの単純なアルゴリズムです。今回は回転や反転は考慮しません。
pip, import
まだvcoptをpipしていない場合はpipします。
pip install vcopt必要なパッケージをimportします。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcoptペントミノの作成
がんばって手書きしました。各ミノは1~12のIDを並べて表現します。
#===============================================
#ペントミノの作成
#===============================================
def make_pentominos():
pentominos = []
pentominos.append(np.array([[1,1,1,1,1]], dtype=int)) #棒も2次元配列とすること
pentominos.append(np.array([[2,0,0,0],
[2,2,2,2]], dtype=int))
pentominos.append(np.array([[0,0,3,0],
[3,3,3,3]], dtype=int))
pentominos.append(np.array([[0,0,4,4],
[4,4,4,0]], dtype=int))
pentominos.append(np.array([[5,0,5],
[5,5,5]], dtype=int))
pentominos.append(np.array([[0,6,6],
[6,6,6]], dtype=int))
pentominos.append(np.array([[0,0,7],
[0,0,7],
[7,7,7]], dtype=int))
pentominos.append(np.array([[0,8,8],
[0,8,0],
[8,8,0]], dtype=int))
pentominos.append(np.array([[9,9,9],
[0,9,0],
[0,9,0]], dtype=int))
pentominos.append(np.array([[ 0,10,10],
[10,10, 0],
[ 0,10, 0]], dtype=int))
pentominos.append(np.array([[ 0,11, 0],
[11,11,11],
[ 0,11, 0]], dtype=int))
pentominos.append(np.array([[12, 0, 0],
[12,12, 0],
[ 0,12,12]], dtype=int))
return pentominos
#ペントミノの作成
pentominos = make_pentominos()
print(pentominos)[array([[1, 1, 1, 1, 1]]),
array([[2, 0, 0, 0],
[2, 2, 2, 2]]),
array([[0, 0, 3, 0],
[3, 3, 3, 3]]),
array([[0, 0, 4, 4],
[4, 4, 4, 0]]),
array([[5, 0, 5],
[5, 5, 5]]),
array([[0, 6, 6],
[6, 6, 6]]),
array([[0, 0, 7],
[0, 0, 7],
[7, 7, 7]]),
array([[0, 8, 8],
[0, 8, 0],
[8, 8, 0]]),
array([[9, 9, 9],
[0, 9, 0],
[0, 9, 0]]),
array([[ 0, 10, 10],
[10, 10, 0],
[ 0, 10, 0]]),
array([[ 0, 11, 0],
[11, 11, 11],
[ 0, 11, 0]]),
array([[12, 0, 0],
[12, 12, 0],
[ 0, 12, 12]])]はい、こんな感じです。
Bottom-Left法で敷き詰める
#===============================================
#敷き詰める順序を受け取り、Bottom-Left法で左上から敷き詰め、フィールドを返す
#===============================================
def bottom_left(para):
#フィールドの作成(高さは多めにとっておく)
f = np.zeros((30, w), dtype=int)
#paraの順序にしたがってBottom-Left法で左上から敷き詰める
for n in para:
pentomino = pentominos[n]
next_mino = False
#左上から順番に、入れられるかチェック
for i in range(30):
for j in range(w):
#ミノの幅、高さ
p_h, p_w = pentomino.shape
#幅がフィールドを超えてしまうならNG、for文をひとつ抜ける
if w < j + p_w:
break
#入れられるかチェック(該当スペースに掛け算=ANDして、全部0なら入れられる)
#入れられるなら入れて、for文をふたつ抜ける
if np.sum(f[i:i+p_h, j:j+p_w] * pentomino) == 0:
#入れる
f[i:i+p_h, j:j+p_w] += pentomino #代入だとダメ、足す
next_mino = True
break
if next_mino == True:
break
#ミノが置かれている矩形領域を検出
last_line = np.where(f > 0)[0][-1]
#その部分を返す
return f[:last_line + 1, :]
#フィールドの幅
w = 6
#敷き詰める順番(ID順)
para = range(12)
#敷き詰めてみる
print(bottom_left(para))[[ 1 1 1 1 1 0]
[ 2 0 0 0 0 0]
[ 2 2 2 2 3 0]
[ 0 0 3 3 3 3]
[ 0 0 4 4 0 0]
[ 4 4 4 5 0 5]
[ 0 6 6 5 5 5]
[ 6 6 6 7 0 0]
[ 0 0 0 7 8 8]
[ 0 7 7 7 8 0]
[ 9 9 9 8 8 0]
[ 0 9 0 10 10 0]
[ 0 9 10 10 0 0]
[ 0 11 0 10 0 0]
[11 11 11 12 0 0]
[ 0 11 0 12 12 0]
[ 0 0 0 0 12 12]]ミノ1番から順番に敷き詰めた場合のフィールドが返ってきました。
敷き詰めてグラフを表示
#===============================================
#敷き詰める順序を受け取り、Bottom-Left法で左上から敷き詰め、敷き詰めて表示
#===============================================
def BL_show(para):
#paraの順番に敷き詰める
f = bottom_left(para)
#表示
plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='gist_ncar_r', vmin=0)
plt.show(), print()
#敷き詰める順番(ID順)
para = range(12)
#敷き詰めて表示
BL_show(para)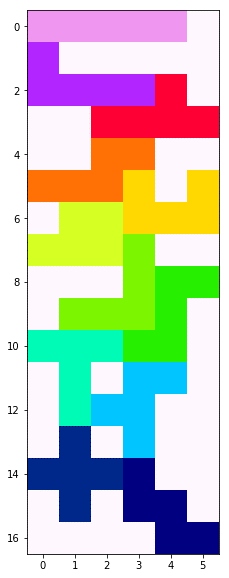
ミノ1番から順番に敷き詰めた場合、かなり隙間があります。
敷き詰めてスコア(隙間の数)を返す
#===============================================
#敷き詰める順序を受け取り、Bottom-Left法で左上から敷き詰め、隙間の数をスコアとして返す
#===============================================
def BL_score(para, **info):
#paraの順番に敷き詰める
f = bottom_left(para)
#隙間の数
score = np.sum(f == 0)
return score42隙間の数は42個のようです。このあと、これが0に近づくように最適化します。
2-opt法で局所最適化
#===============================================
#2-opt法で局所最適化
#===============================================
#para初期値
para = range(12)
#2-opt法で局所最適化
para, score = vcopt().opt2(para, #並び替えたい要素の1次元配列
BL_score, #評価関数
0.0) #評価値をいくつに近づけるか
#結果の表示
print(para)
print(score)
BL_show(para)[ 1 0 2 3 10 5 8 9 6 7 4 11]
18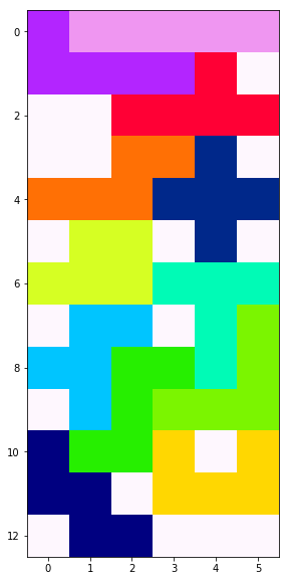
処理中の乱数によって異なるスコアが出ますが、隙間が18個まで減りました!
GAで大域最適化
#===============================================
#GAで大域最適化
#===============================================
#paraを並べたもの
para_range = range(12)
#GA
para, score = vcopt().tspGA(para_range, #paraを並べたもの
BL_score, #評価関数
0.0, #評価値をいくつに近づけるか
show_pool_func='print', #簡易表示機能を使う
pool_num=20) #個体数をデフォルトの120から20に減らす
#結果の表示
print(para)
print(score)
BL_show(para)gen=0, best_score=24.0, mean_score=31.5, mean_gap=31.5, time=2.55
gen=20, best_score=18.0, mean_score=21.6, mean_gap=21.6, time=3.84
gen=40, best_score=12.0, mean_score=18.9, mean_gap=18.9, time=6.03
gen=60, best_score=12.0, mean_score=17.7, mean_gap=17.7, time=8.81
gen=80, best_score=12.0, mean_score=17.4, mean_gap=17.4, time=11.51
gen=100, best_score=12.0, mean_score=17.1, mean_gap=17.1, time=14.25
gen=120, best_score=12.0, mean_score=17.1, mean_gap=17.1, time=16.77
[ 1 3 10 6 2 8 7 9 11 5 4 0]
12.0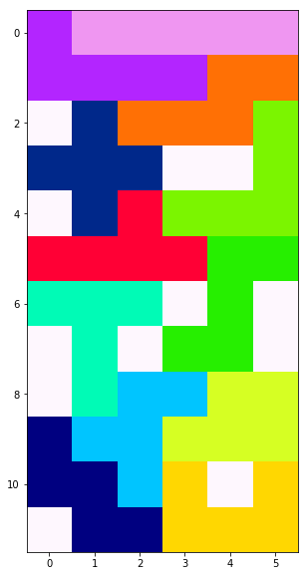
隙間が12個まで減りました!やはりGAは有効のようです!
まとめ
敷き詰め問題には有力な解法がありません(あったら教えてください!(切実))。次回は、回転と反転を考慮したGAに挑戦したいです。



