8-2. 遺伝的アルゴリズム（vcopt）で巡回セールスマン問題を解く（2-opt法編）

GA / vcopt

2019/03/20

本記事の内容は2019年5月13日に更新されました。

やること
実行環境
import
巡回セールスマン問題の作成
ランダムな道順で歩いてみる
（必須）評価関数
（任意）ひとつのパラメータ群を可視化する関数
2-opt法で局所最適化

やること

vcoptには、GAの他に局所最適化アルゴリズムが付属しています。GAの性能を見る前に、まずは巡回セールスマン問題の局所最適化を試してみましょう。ここで作成した関数は次回以降のGAでも使えますので。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

vcoptの使い方についてはチュートリアルをご参照ください。

vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。

import

まずは、今回使うパッケージをインポートします。

import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcopt

巡回セールスマン問題の作成

問題を用意します。この関数は、「町の数」を受け取って、各町の「x座標の配列」と「y座標の配列」を返します（ランダム生成）。

#巡回セールスマン問題の作成
def create_tsp(town_num):
    
    #町のx座標とy座標の配列を作成
    town_x = nr.rand(town_num)
    town_y = nr.rand(town_num)
    
    return town_x, town_y

この関数で問題を作成し、プロットしてみましょう。乱数シードを固定すると毎回同じ結果が得られます。

#巡回セールスマン問題の作成
nr.seed(1)
town_num = 20
town_x, town_y = create_tsp(town_num)

#プロット
plt.figure(figsize=(6, 6))
plt.plot(town_x, town_y, 'ok')
plt.xlabel('x'); plt.ylabel('y')
plt.xlim([0, 1]); plt.ylim([0, 1])
plt.show()

実行結果

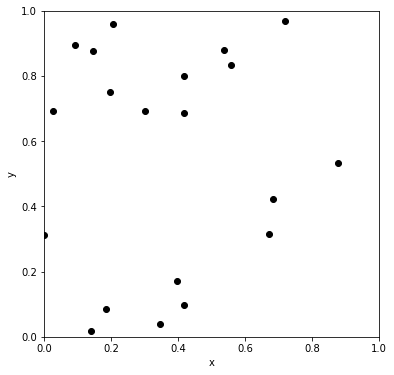
ランダムな道順で歩いてみる

town_xをある道順に従って並び替えるには、town_x[道順]のようにします。town_yも同様です。

#巡回セールスマン問題の作成
nr.seed(1)
town_num = 20
town_x, town_y = create_tsp(town_num)

#ランダムな道順の作成
para = np.arange(town_num)
nr.shuffle(para)
print(para)

#プロット
plt.figure(figsize=(6, 6))
plt.plot(town_x[para], town_y[para], 'ok-')
plt.xlabel('x'); plt.ylabel('y')
plt.xlim([0, 1]); plt.ylim([0, 1])
plt.show()

実行結果

[18 16  1 12 17  5 11 13  3  6  8  9 10 14  7  2 19  4  0 15]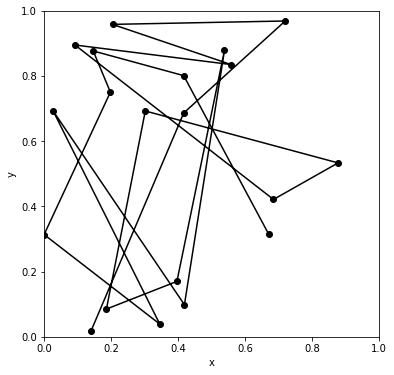

（必須）評価関数

パラメータ群を入れると評価（スコア）が返ってくるような関数を用意します。最適化では、このスコアが小さくなるように（or 大きくなるように or 特定の値に近づくように）パラメータ群を変化させます。

評価関数にはルールがあります。必ず次の形式に従ってください。

#巡回セールスマン問題の評価関数
def 関数名(para):

    #スコアの計算
    score = ...
    
    return score

この形式に従い、すべての町を訪れる際の総距離を返す評価関数はこうなります。

#巡回セールスマン問題の評価関数
def tsp_score(para):
    
    #スコアの計算（今回は直接returnする）
    
    return np.sum(((town_x[para][:-1] - town_x[para][1:])**2 + (town_y[para][:-1] - town_y[para][1:])**2)**0.5)

ちょっとスコア計算の式がわかりにくいと思いますが、２点間の距離を配列のまま一度に算出して、sumしています。

（任意）ひとつのパラメータ群を可視化する関数

もう最適化は実行できるのですが、最適化の様子を可視化するための関数を用意しておきましょう。

可視化のための関数にもルールがあります。必ず次の形式に従ってください。

#巡回セールスマン問題の可視化
def 関数名(para, **info):
    
    #2-opt処理中の諸情報はinfoという辞書に格納されて渡されます
    #これらを受け取って使用することができます
    step_num = info['step_num']
    score = info['score']
    
    #可視化
    ...

この形式に従うと、すべての町を訪れる道順を可視化する関数はこうなります。お好みでstep_numとscoreも使用できます。

#paraの可視化
def tsp_show_para(para, **info):
    
    #2-opt処理中の諸情報はinfoという辞書に格納されて渡されます
    #これらを受け取って使用することができます
    step_num = info['step_num']
    score = info['score']
    
    #プロット（および保存）
    plt.figure(figsize=(6, 6))
    plt.plot(town_x[para], town_y[para], 'ok-')
    plt.xlabel('x'); plt.ylabel('y')
    plt.xlim([0, 1]); plt.ylim([0, 1])
    plt.title('step={}, score={}'.format(step_num, score))
    #plt.savefig('save/{}.png'.format(step_num))
    plt.show()
    print()

2-opt法で局所最適化

いよいよ最適化を実行します。

#巡回セールスマン問題の作成
nr.seed(1)
town_num = 20
town_x, town_y = create_tsp(town_num)

#適当に道順を作成
para = np.arange(town_num)

#2-opt法で最適化
para, score = vcopt().opt2(para,                          #para
                           tsp_score,                     #score_func
                           0.0,                           #aim
                           show_para_func=tsp_show_para,  #show_para_func=None
                           seed=1)                        #seed=None

#結果の表示
print(para)
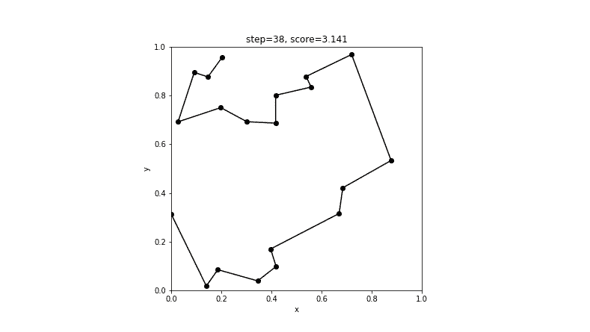
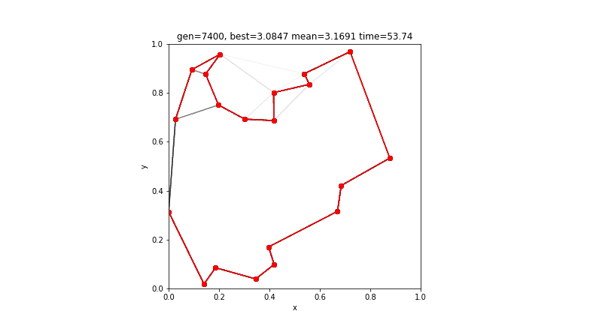
print(score)

実行結果

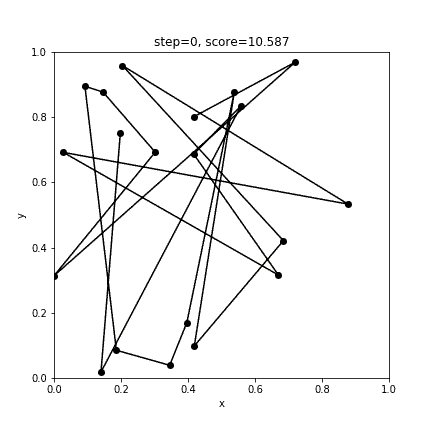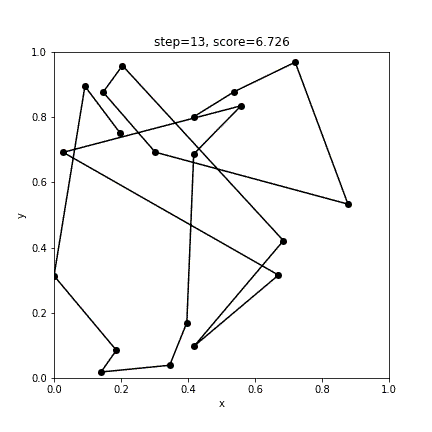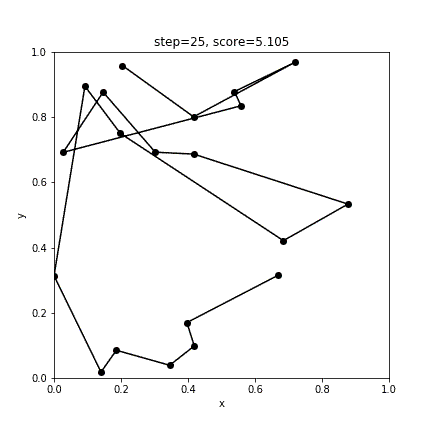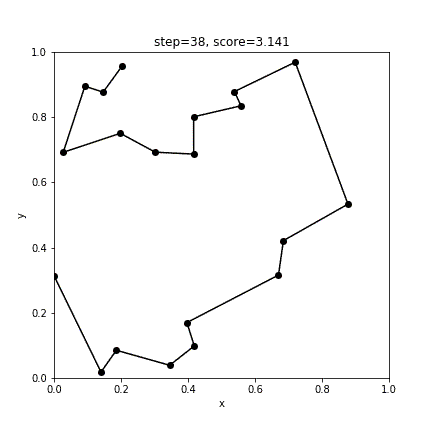
[12  4  5 14 19  3 16  0 17  9  1 13 11 15  8 10  7  6 18  2]
3.140836748527908

38回の更新で、最短距離3.141のルートが返ってきました。