9-23. NKランドスケープ問題を全探索と遺伝的アルゴリズムで解く

やること

NKランドスケープ（NKモデル）は N と K の２つの変数でお手軽に難易度を調整できる組合せ最適化問題で、最適化アルゴリズムのためのベンチマーク問題として用いられます。

今回はNKランドスケープ問題（以下、NK問題）の生成と、全探索および遺伝的アルゴリズムでの探索の速度を比較してみます。

NK問題とは

英語のWikipediaはありましたが、日本語のサイトは少ないようです。

NK model - Wikipedia

en.wikipedia.org

NK問題における配列とその評価値の計算方法を確認しておきます。例として N = 6, K = 2 の問題を用意しました。「遺伝子」という言葉を使ったGA寄りの説明になっていますのでご了承を。

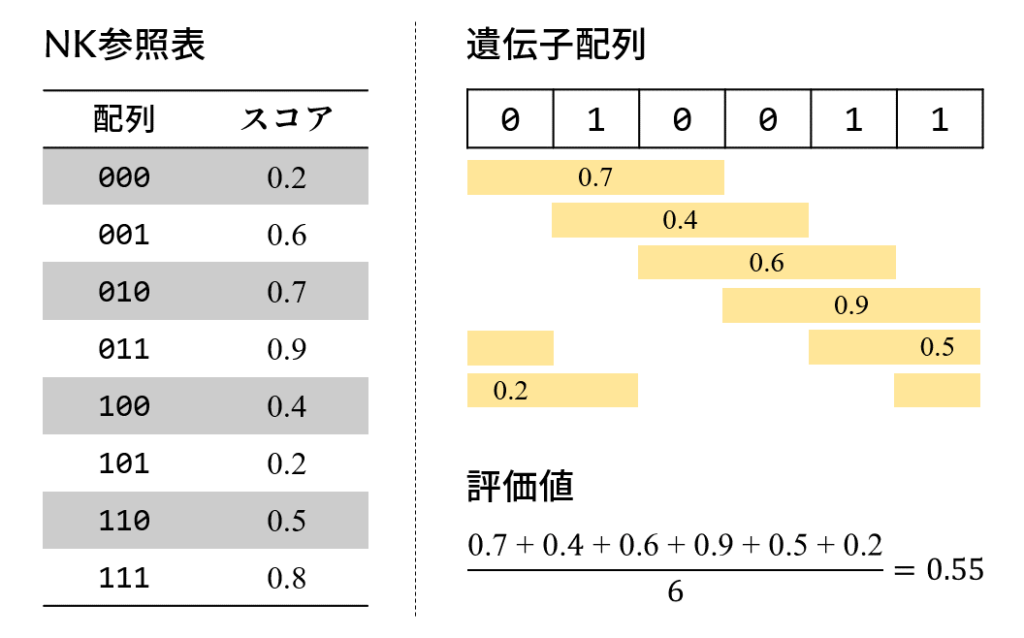
０または１の遺伝子からなる長さ N の遺伝子配列 [0, 1, 0, 0, 1, 1] があるとします。この配列の遺伝子を左から３個ずつセットにして切り出し、参照表に当てはめながらスコアを足していきます。遺伝子配列の両端はループしています。スコアの合計値を N で割った「遺伝子１個あたりの平均スコア」が遺伝子配列の評価値となります。上の例では0.55で、0 ≦ 評価値 ≦ 1 となります。

N は遺伝子配列の長さ、K は遺伝子がもつれ合う長さを意味します。ややこしいのですが、K = 0 のときは隣とのもつれがなく、切り出す遺伝子長は１です。K = 2 であれば２本の手を繋いでいると考えて３個を切り出します。K = N – 1 で遺伝子配列全体がもつれることから分かるように、K < N に限ります。

NK参照表はもつれる遺伝子のすべての組み合わせにスコアが対応付けられたもので、スコアは０～１の一様乱数です。参照表の行数は ２^k+1 行になります。

実のところNK問題の本体はこのNK参照表です。表だけで問題になるのかよ！と思ってしまいますが、これが複雑な解空間を生み出すのです。なぜ複雑になるのかというと、一つの遺伝子を反転させて評価値を上げようとしても、もつれた範囲のスコアがガラッと変わってしまうため思うように評価値が上がりません。より高い評価値を得るには複数の遺伝子を一度に反転させなければなりませんが、その見当が付けられません。このような原理で、配列長（N）ともつれ範囲（K）が大きいほど複雑な（多峰性の）解空間になるのです。

余談ですが、K = 0 のとき、参照表は ‘0’ と ‘1’ の２行だけで、大域解は [0, 0, 0, 0, 0, 0] または [1, 1, 1, 1, 1, 1] のどちらかになります。これはOne-max問題（単峰性）と同義であり、NK問題はOne-max問題を内包していると言えます。また K = 2 のときも、’000′ または ‘111’ が最高スコアを持っていた場合、最適解は [0, 0, 0, 0, 0, 0] または [1, 1, 1, 1, 1, 1] になります。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

sourceforge.net

Google Colaboratoryが利用可能です。

Google Colab

colab.research.google.com

vcoptの使い方についてはチュートリアルをご参照ください。

お手軽最適化パッケージ「vcopt」チュートリアル

実行環境Windowsマシンで実行する方にはWinPython3.6をおすすめしています。インストール不要で、USBメモリに入れて持ち運ぶこともできます。...

vigne-cla.com

2019/09/23

vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。

お手軽最適化パッケージ「vcopt」仕様書

はじめにvcoptとは遺伝的アルゴリズム（Genetic Algorithm, GA）による本格的な組合せ最適化がお手軽にできる無料のPythonパッケージで...

vigne-cla.com

2019/09/22

pipインストール

vcoptをインストールします。

pip install vcopt

NK問題の作成

再現性のためここでは乱数シードを固定して問題を生成します。

import time
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcopt


#=============================
# NK問題のパラメータ
#=============================
N = 6
K = 2


#=============================
# NK問題の作成
#=============================
#実験のため乱数シードを固定
nr.seed(3)

#ウィンドウサイズ
window_size = K + 1

#ビット全組み合わせ
bit_list = ['{:b}'.format(i).zfill(window_size) for i in range(2**window_size)]
print('bit_list:\n{}'.format(bit_list))

#乱数スコア列
score_list = nr.rand(2**window_size)
print('score_list:\n{}'.format(score_list))

#NKテーブル
table = dict(zip(bit_list, score_list))
print('table:\n{}'.format(table))

bit_list:
['000', '001', '010', '011', '100', '101', '110', '111']
score_list:
[0.5507979  0.70814782 0.29090474 0.51082761 0.89294695 0.89629309
 0.12558531 0.20724288]
table:
{'000': 0.5507979025745755, '001': 0.7081478226181048, '010': 0.2909047389129443, '011': 0.510827605197663, '100': 0.8929469543476547, '101': 0.8962930889334381, '110': 0.12558531046383625, '111': 0.20724287813818676}

問題ができました。NK参照表は「table」に辞書型として格納されています。

大域解の探索

大域解を全探索で調べます。

#=============================
# 大域解の探索
#=============================
#遺伝子全組み合わせ
gene_list = ['{:b}'.format(i).zfill(N) for i in range(2**N)]
print('gene_list:\n{}'.format(gene_list))

#全探索準備
best_gene = ''
best_score = 0
gene_list_double = np.core.defchararray.add(gene_list, gene_list) #処理のための倍化配列
#print('gene_list_double:\n{}'.format(gene_list_double))
#全探索
start = time.time()
for gene in gene_list_double:
    #単一の遺伝子配列のスコア計算
    score = 0
    for i in range(0, N):
        score += table[gene[i:i+window_size]]
    score /= N
    if score > best_score:
        best_gene = gene
        best_score = score
print('best_gene:\n{}'.format(best_gene[:N]))
print('best_score:\n{}'.format(best_score))

#全探索時間の表示
end = time.time()
print('time:\n{}s'.format(round(end - start, 2)))

gene_list:
['000000', '000001', '000010', '000011', '000100', '000101', '000110', '000111', '001000', '001001', '001010', '001011', '001100', '001101', '001110', '001111', '010000', '010001', '010010', '010011', '010100', '010101', '010110', '010111', '011000', '011001', '011010', '011011', '011100', '011101', '011110', '011111', '100000', '100001', '100010', '100011', '100100', '100101', '100110', '100111', '101000', '101001', '101010', '101011', '101100', '101101', '101110', '101111', '110000', '110001', '110010', '110011', '110100', '110101', '110110', '110111', '111000', '111001', '111010', '111011', '111100', '111101', '111110', '111111']
best_gene:
001001
best_score:
0.6306665052929014
time:
0.0s

探索すべき配列は ２^N 通りありますので、N が大きくなると指数的に探索時間が伸びていきます。今回は０秒で大域解 [0, 0, 1, 0, 0, 1] が見つかりました。

ちなみに、遺伝子配列の両端はループしているので回転すると重複する配列があります（cf. 円順列）。これらの重複を除けばもっと速く探索が終わりますが、ここでは簡便さを優先しています。

GAのための評価関数

vcoptのルールに従い、para（遺伝子配列）を受け取って評価値を返す関数を作ります。

#=============================
# 評価関数
#=============================
def gene_score(para):
    #paraをくっつけて文字列に
    gene = ''.join(map(str, para))
    
    #遺伝子配列のスコア計算
    gene_double = gene + gene
    score = 0
    for i in range(0, N):
        score += table[gene_double[i:i+window_size]]
    score /= N
    
    #スコアを返す
    return score

#適当な遺伝子配列を生成して動作確認
para = nr.randint(0, 2, N)
print('para:\n{}'.format(para))
print('gene_score(para):\n{}'.format(gene_score(para)))

para:
[1 0 0 0 0 1]
gene_score(para):
0.5565172496294016

適当な遺伝子配列を生成して入れてみると、評価値0.557が返ってきました。

GAで最適化

vcoptのGA設計は 「vcopt」仕様書 に書かれていますが、個体数が10n（nは次元数、ここではNK問題のNに等しい）、親２、子４、一点交叉と二点交叉を組み合わせた交叉法、復元抽出にエリート選択です。

#=============================
# GAで最適化
#=============================
#para_range
para_range = np.array([[0, 1] for j in range(N)])
#GAの実行
para, score = vcopt().dcGA(para_range,              #遺伝子の範囲
                           gene_score,              #評価関数
                           best_score,              #評価値の目標値（さっき求めた大域解）
                           show_pool_func='print')  #表示オプション

________________________________________ info ________________________________________
para_range     : n=6
score_func     : <class 'function'>
aim            : ==0.6306665052929014
show_pool_func : 'print'
seed           : 0
pool_num       : 60
max_gen        : None
core_num       : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 60/60        
gen=       0, best_score=   0.631, mean_score=   0.517, mean_gap=   0.114, time=   0.0
gen=      60, best_score=   0.631, mean_score=   0.577, mean_gap=   0.053, time=   0.0
_______________________________________ result _______________________________________
para = np.array([0, 0, 1, 0, 0, 1])
score = 0.6306665052929014
________________________________________ end _________________________________________

０秒で大域解 [0, 0, 1, 0, 0, 1] が見つかりました。

注意点として、N や K を大きくして試す場合は配列関連の print() をコメントアウトしてください。表示が多すぎてコンソールがバグります。

全探索とGAはどちらが速いのか

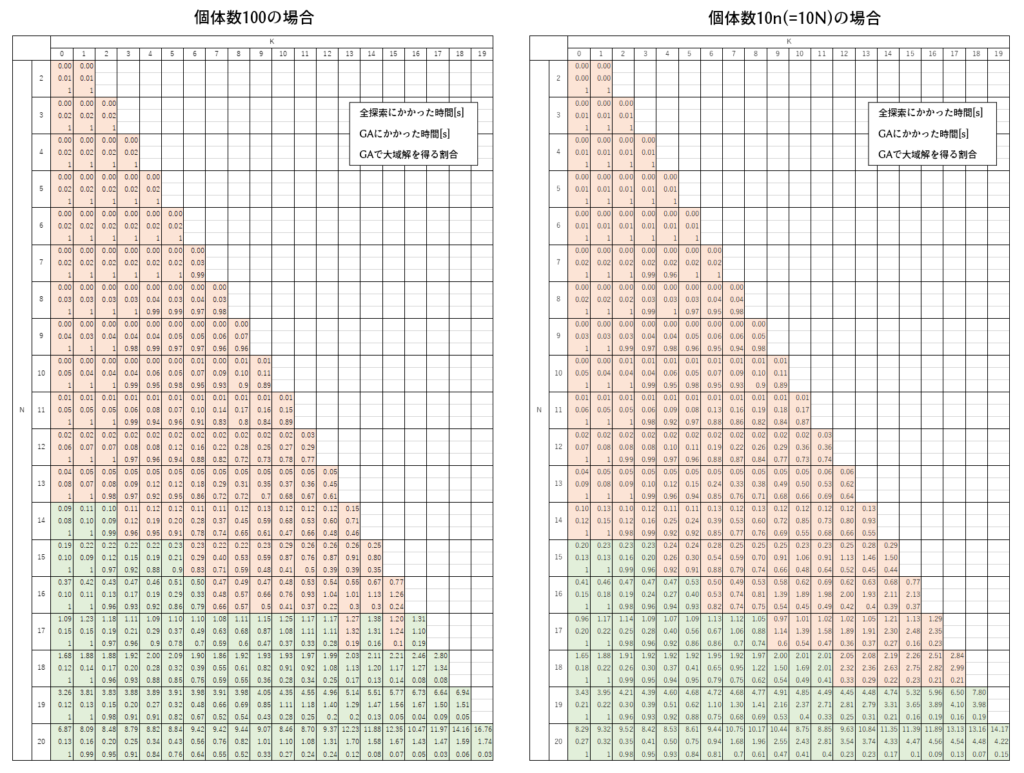
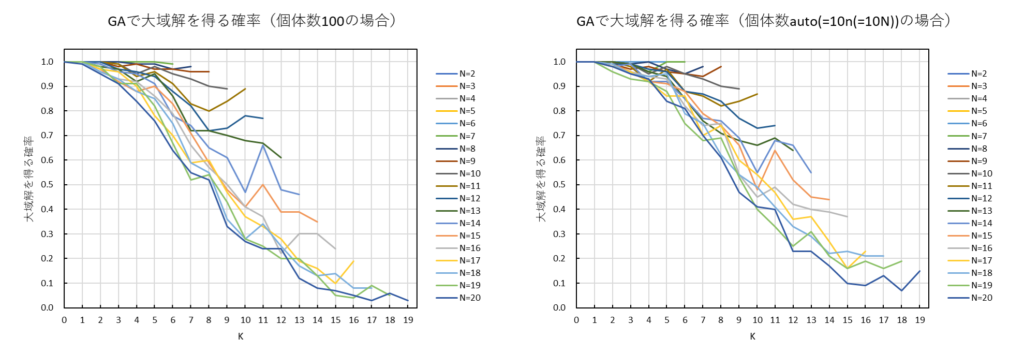
2 ≦ N ≦ 20、0 ≦ K < N の範囲で100回ずつ問題作成→全探索→GAを行ってみました。今回は研究のため、GAの個体数を100に固定した場合（左）と自動設定モードの場合（右）を並べています。vcoptは「pool_num=100」のオプションで個体数を指定できます。

探索速度について、詳細は画像をクリックして飛んでください。言語、アルゴリズム、CPU性能等によりますので参考程度に。

オレンジは全探索の方が早い領域、緑はGAの方が早い領域です。N が大きくなると全探索時間は指数的に長くなりますが、GAにかかる時間の伸びは比較的穏やかで、速度の優位性が逆転するラインが生じます。しかし、GAは大域解が見つかる確率も下がります。N = 20, K = 19 にもなると全探索で14.2秒かかり、GAは4.2秒ですが大域解発見は10%程度になります。大域解に近い局所解は得られているのですが。GAはメタヒューリスティックな手法なので「近似解で良いから早く求めたい」ときに重宝するということを再確認できる結果です。

また、「GAで大域解が見つかる確率」をプロットしました。

この規模のNK問題では、個体数は100でも10n(=10N)でもさほど変わらない印象です。N = 20 のとき最大５％高まる程度のよう。恐るべしNK問題、軽くひねり潰されました。。

まとめ

皆さんにNK問題の単純さと奥深さが伝わると嬉しいです。

余談ですが「研究者は実社会にない問題を作ってそれを解いて満足している」という旨のツイートを見かけました。NK問題もまさにそう捉えられていると思います。

しかしこれはまったく当たらない指摘です。研究は過去の研究からの積み上げですから、共通の問題を解いて厳密に比較・解析しながら議論をしなければなりません。そのために研究者は「難易度が調整可能なベンチマーク問題」をいくつも発明してきました。NK問題は実社会に直接的に役立つものではありませんが、多数の研究者が共通の積み木を積み上げるために必須の存在なのです。