やること
ライフゲーム( Conway’s Game of Life )は生命の誕生、進化、淘汰などのプロセスを非常に簡単な数理モデルで表現したシミュレーションゲームです。 Pythonではfor文1回だけでライフゲームが楽しめますので、一緒にやってみましょう。
参考文献
基本のルールについてはWikipedia、あとは複雑系コミュニティ動画さんのシリーズがおすすめです。とても魅力的にまとめられています。
※クリックでYoutubeにジャンプします
基本のルール
フィールドは正方形のマス目で、各マスの状態が変化するためのルールは次の2つだけです。
| 現在の状態 | 隣接する8セルの条件 | 次の状態 |
| 生存(1) | 生存セルが0~1または4~8個 | 死(0) |
| 死(0) | 生存セルが3個 | 生存(1) |
これに当てはまらない場合は現状維持となります。
別の表現として、生きるための条件に着目して書くとこうなります。
| 次のステップでの生存条件 | |
| 生存セル | 隣接する8セルのうち生存セルが2、3個 |
| 死セル | 隣接する8セルのうち生存セルが3個 |
実行環境
どちらかを用いますが、WinPythonをおすすめします。WinPythonでは図が紙芝居のようにパラパラ流れて見やすいですが、Colabではスクロールする必要があり見づらいです。
Colabにも対応しました!(推奨)
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

ソースコード
前半はフィールドサイズや初期状態の設定です。後半はメインの繰り返し処理で、基本的にいじらなくても大丈夫です。
↓WinPythonコード
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 10, 10
#任意の状態を用意
state = np.array([[0,0,1],
[1,0,1],
[0,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (0, 0)
#終了ステップ数
max_step = 35
#============================
#メイン処理
#============================
#フィールドの生成
f = np.zeros((h, w), dtype=bool)
#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state
#初期状態の表示
#plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='inferno')
#plt.savefig('save/{}.png'.format(0), bbox_inches='tight', pad_inches=0)
plt.show(), print()
#状態の更新
for i in range(1, max_step + 1):
#周囲の生存マス数を記録するための配列
mask = np.zeros((h, w))
#周囲の生存マスを足し込む
mask[1:, :] += f[:-1, :] #上
mask[:-1, :] += f[1:, :] #下
mask[:, 1:] += f[:, :-1] #左
mask[:, :-1] += f[:, 1:] #右
mask[1:, 1:] += f[:-1, :-1] #左上
mask[1:, :-1] += f[:-1, 1:] #右上
mask[:-1, 1:] += f[1:, :-1] #左下
mask[:-1, :-1] += f[1:, 1:] #右下
#未来のフィールド(すべて死状態)
future = np.zeros((h, w), dtype=bool)
#生きているマスが生きる条件(=生存)
future[mask*f==2] = 1
future[mask*f==3] = 1
#死んでいるマスが生きる条件(=誕生)
future[mask*~f==3] = 1
#フィールドの更新(浅いコピーに注意)
f = future
#表示
#plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='inferno')
#plt.savefig('save/{}.png'.format(i), bbox_inches='tight', pad_inches=0)
plt.show(), print()↓Colabコード
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from matplotlib import animation, rc
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 10, 10
#任意の状態を用意
state = np.array([[0,0,1],
[1,0,1],
[0,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (0, 0)
#終了ステップ数
max_step = 35
#============================
#メイン処理
#============================
#フィールドの生成
f = np.zeros((h, w), dtype=bool)
#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state
#画像をスタックする配列の準備
fig = plt.figure()
#fig = plt.figure(figsize=(10, 10))
ims = []
#初期状態の表示(スタック)
im = plt.imshow(f, cmap='inferno')
ims.append([im])
#状態の更新
for i in range(1, max_step + 1):
#周囲の生存マス数を記録するための配列
mask = np.zeros((h, w))
#周囲の生存マスを足し込む
mask[1:, :] += f[:-1, :] #上
mask[:-1, :] += f[1:, :] #下
mask[:, 1:] += f[:, :-1] #左
mask[:, :-1] += f[:, 1:] #右
mask[1:, 1:] += f[:-1, :-1] #左上
mask[1:, :-1] += f[:-1, 1:] #右上
mask[:-1, 1:] += f[1:, :-1] #左下
mask[:-1, :-1] += f[1:, 1:] #右下
#未来のフィールド(すべて死状態)
future = np.zeros((h, w), dtype=bool)
#生きているマスが生きる条件(=生存)
future[mask*f==2] = 1
future[mask*f==3] = 1
#死んでいるマスが生きる条件(=誕生)
future[mask*~f==3] = 1
#フィールドの更新(浅いコピーに注意)
f = future
#表示(スタック)
im = plt.imshow(f, cmap='inferno')
ims.append([im])
#アニメーション表示の準備
print('making animation......')
print('len(ims) = ' + str(len(ims)))
ani = animation.ArtistAnimation(fig, ims, interval=50, blit=True)
#ここにアニメを表示する場合はこちらを有効に
rc('animation', html='jshtml')
ani
#.gifや.mp4を保存する場合はこちらを有効に
#ani.save('aaa.gif', writer='imagemagick',fps=40)
#ani.save('bbb.mp4', writer="ffmpeg")for文を1回(1重)しか使っていない点にご注目ください。Pythonは2次元配列を配列のまま足したり掛けたりできる強みがあります。for文をいくつもネストしてしまうと計算が極端に遅くなりますので、避けなければなりません。
※上記は一般論です。ライフゲームはほとんどのマスが0のため、「1のマスだけ処理する」といった処理のほうが高速化に寄与する可能性があります。
グライダーで実行してみる
ソースコードをそのまま実行すると、フィールドの左上からグライダーが進み始めます。
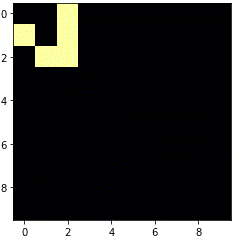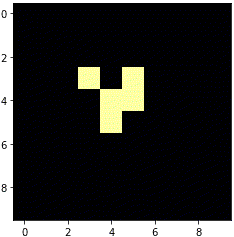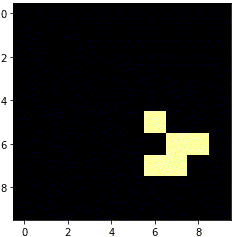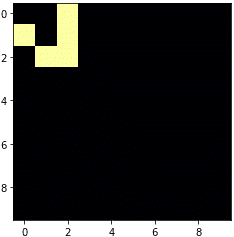
銀河
かっこいいです。
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 15, 15
#任意の状態を用意
state = np.array([[1,1,0,1,1,1,1,1,1],
[1,1,0,1,1,1,1,1,1],
[1,1,0,0,0,0,0,0,0],
[1,1,0,0,0,0,0,1,1],
[1,1,0,0,0,0,0,1,1],
[1,1,0,0,0,0,0,1,1],
[0,0,0,0,0,0,0,1,1],
[1,1,1,1,1,1,0,1,1],
[1,1,1,1,1,1,0,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (3, 3)
#終了ステップ数
max_step = 15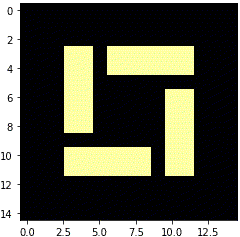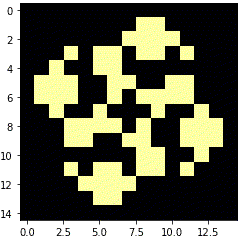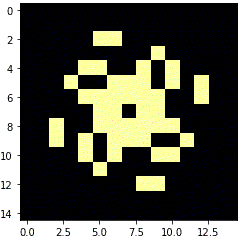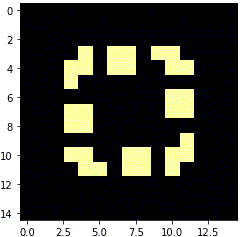
ダイハード
ダイハードは7セルから始まって130ステップも長生きするパターンです。
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 25, 25
#任意の状態を用意
state = np.array([[0,0,0,0,0,0,1,0],
[1,1,0,0,0,0,0,0],
[0,1,0,0,0,1,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (5, 9)
#終了ステップ数
max_step = 135十字スタート
大きなフィールドで十字型にスタートしてみましょう。
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 401, 401
#任意の状態を用意
state = np.zeros((h, w))
state[200, :] = 1
state[:, 200] = 1
#フィールドのどこに置くか(左上点を指定)
p = (0, 0)
#終了ステップ数
max_step = 135WinPythonの場合は、2箇所あるplt.imshowの直前に以下を挿入することで図のサイズを大きくできます。細い線が潰れて見えなくなることを防ぎます。
plt.figure(figsize=(10, 10))Colabの場合は、以下の部分を切り替えてください。
#画像をスタックする配列の準備
#fig = plt.figure()
fig = plt.figure(figsize=(10, 10))
ims = []おわりに
こんな感じで、Wikipediaに載っているパターンをいろいろ試してみると楽しいでしょう。グライダー銃やシュシュポッポ列車ができたらぜひSlackで報告してください!または、Twitterでこの記事のURLを添付してつぶやいていただけたら嬉しいです。


