やること
ペニテンテ(Penitentes)は、アンデス山脈などで見られる、地面から雪や氷がニョキニョキ生えてるー!的な自然現象です。


地面から生えるのではなく雪が融けることによって形成されるようで、一旦くぼみができ始めると日光が入り込んで融解が促進される「正のフィードバック」が生じるためと言われています。
今回はペニテンテをセルオートマトンで簡略的にモデル化し、シミュレーションしてみます。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

モデル
「雪(bool)」と「雪の耐久値(float)」をそれぞれ2次元配列で用意し、ライフゲームのように各セルを更新していきます。以下は実際のペニテンテの原理に忠実に則ったものではありませんので、簡略的なモデルとお考えください。
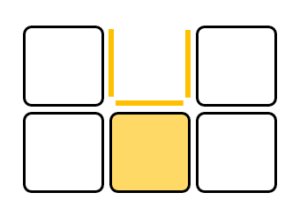
まず、雪を融かす要因として、雪マスの上側のU字型の空間に着目します。このような形状がある場合、壁から反射してきた日光によって融解が促進されると考えられるため、オレンジ線1本につき雪の耐久値が -0.1 されるとします。
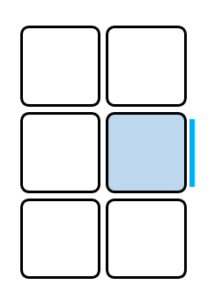
次に、雪を強固にする要因として、雪マスの側面に着目します。このように側面が空いている場合、横殴りの吹雪によって雪が融けにくくなると考え、青線1本につき雪の耐久値が +0.1 されるとします。
あまり厳密に考えないで、アバウトに行きます。次のような雪の状態を考え、いくつか適当なセルについて上記の仮定に従って1ステップあたりの雪の耐久値の変化量を書き込みます。
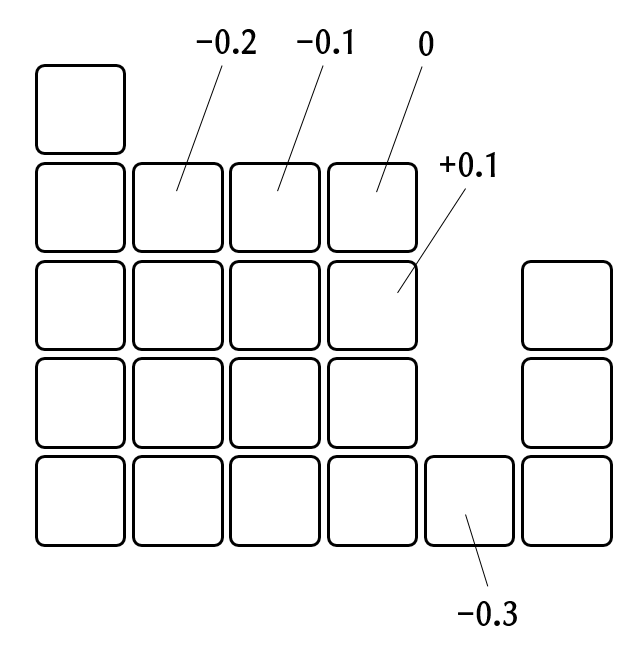
耐久値は0~1の範囲で変動し、0になった雪セルは融けます。
あとは畳み込みのフィルターの各係数をうーんとひねり出します。眠くてひねり出せない場合は連立方程式を立てて解きましょう(モデルがアバウトなので連立方程式もアバウトに解くことが大切です)。こんな感じになりました。
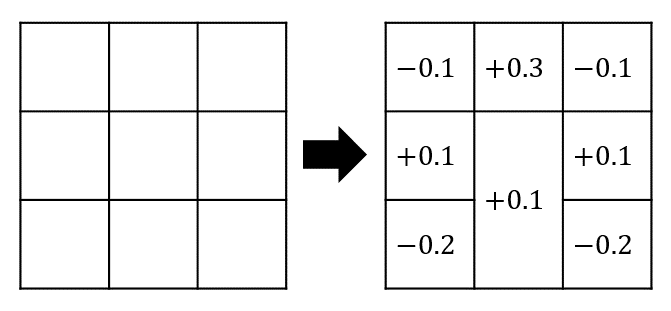
中央と下の係数は一意に定まらず、合計が +0.1 になればいいようです。それではシミュレーションしてみましょう。
コード
おなじみ scipy.signal.convolve2d() を使ってサクッとセルを更新していきます。初期状態をランダムにし、またステップ毎に雪の耐久値にランダムな摂動を加えているので、実行の度に異なる結果になります。詳細はコメントをご参照ください。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from scipy import signal
#============================
# 設定
#============================
#フィールドサイズ
h, w = 50, 100
#============================
# 表示関数
#============================
def show():
plt.figure(figsize=(10, 10))
plt.imshow(s, cmap='Blues', vmin=0, vmax=1)
plt.show(), print()
#============================
# メイン
#============================
#雪の初期化
s = np.ones((h, w), dtype=bool) #0:なし, 1:雪
s[0, :] = 0 #最上段は溶かしておく
s[1, :] = nr.randint(0, 2, w) #2段目はランダムにしておく
#雪の耐久値の初期化
t = np.ones((h, w)) #耐久値は1.0から開始
#畳み込み用フィルタ
f = np.array([[-0.1, +0.3, -0.1],
[+0.1, -0.2, +0.1],
[-0.2, +0.3, -0.2]])
#初期状態の表示
show()
#状態の更新
for step in range(1, 999):
#雪×フィルターで畳み込んで耐久値を更新
t = t + signal.convolve2d(s, f, mode='same', boundary='fill', fillvalue=1) #範囲外は雪ありとする
#耐久値はランダムに減少する(ゆらぎ)
t -= nr.rand(h, w) * 0.01
#耐久値が尽きた雪は融ける
s[t<0] = 0
#耐久値は0~1に収める
t[t<0] = 0
t[t>1] = 1
#表示
show()
#下から5行目が融け始めたら終了
if np.sum(s[-6, :]) < w:
break結果
畳み込みフィルターの中央と下の係数を4パターン試してみました。
中央の係数:-0.2、下の係数:+0.3
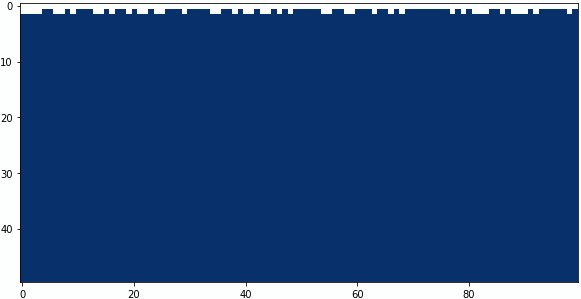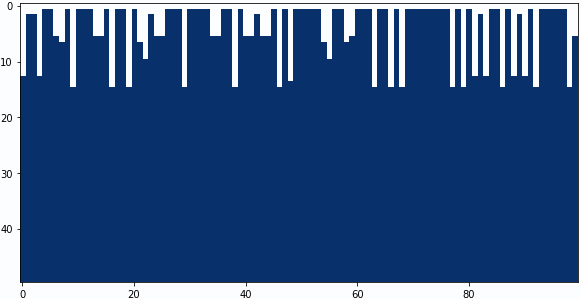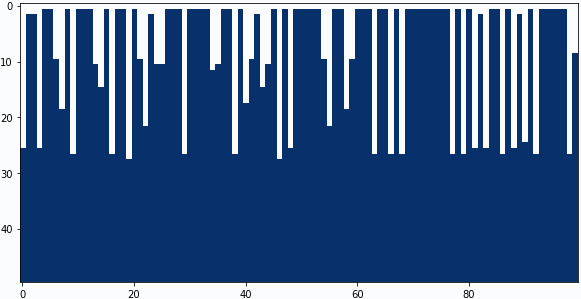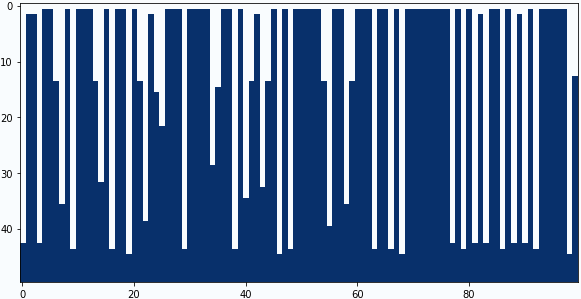
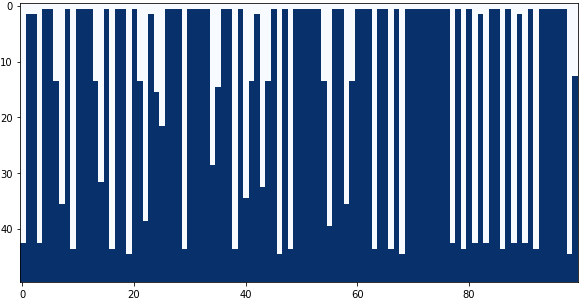
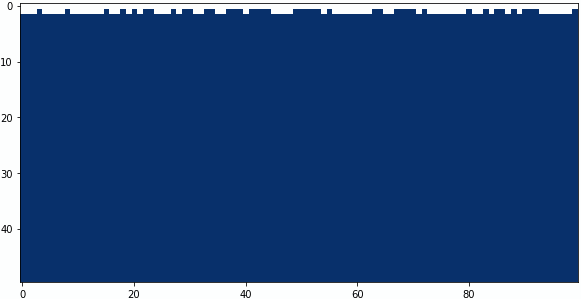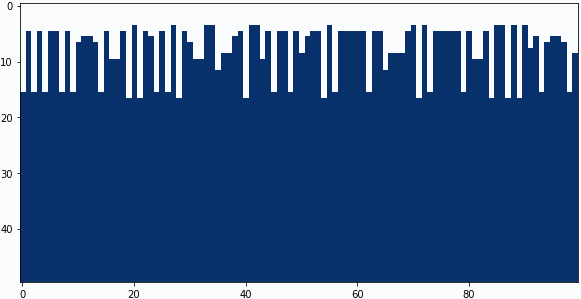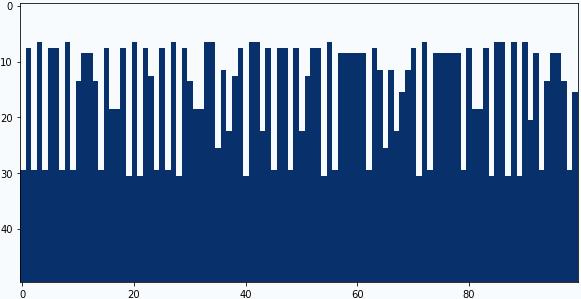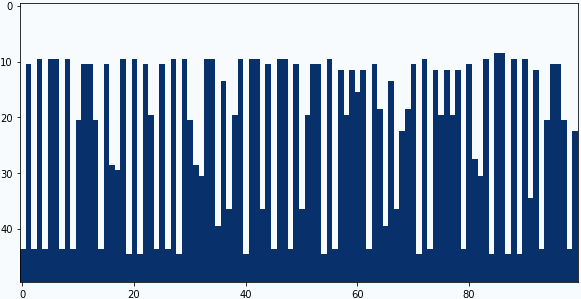
中央の係数:-0.4、下の係数:+0.5
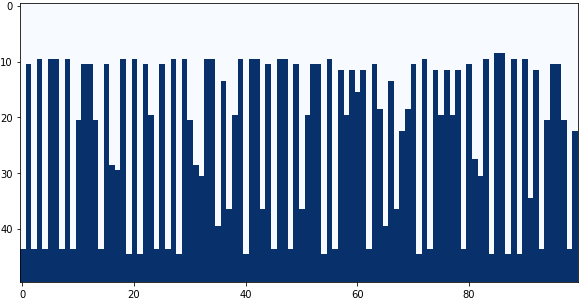
中央の係数:-0.6、下の係数:+0.7
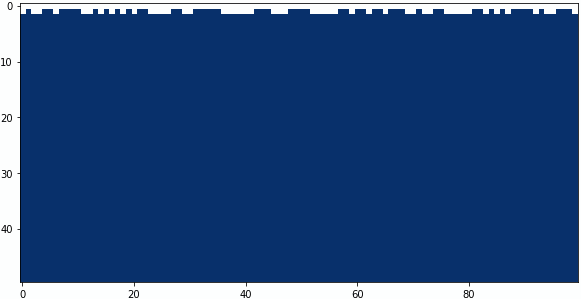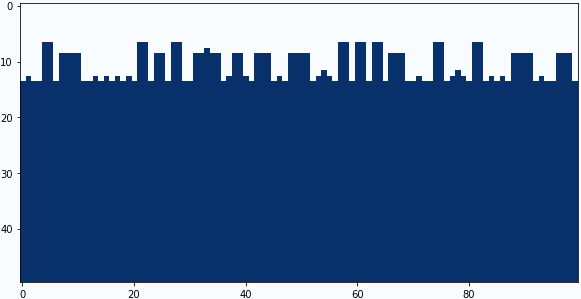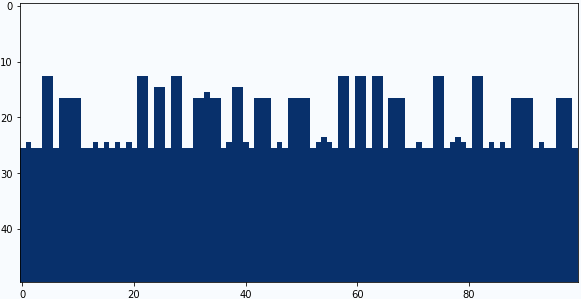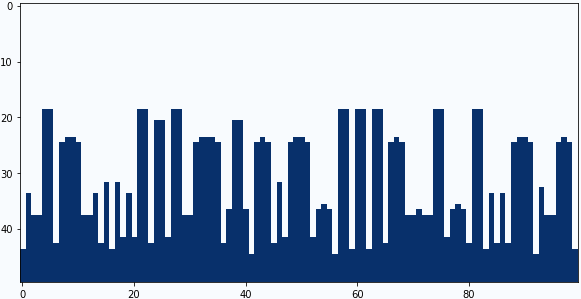
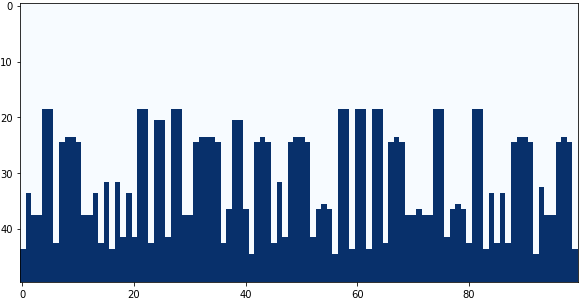
中央の係数:-0.8、下の係数:+0.9
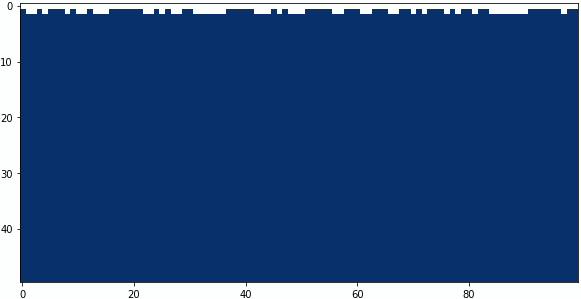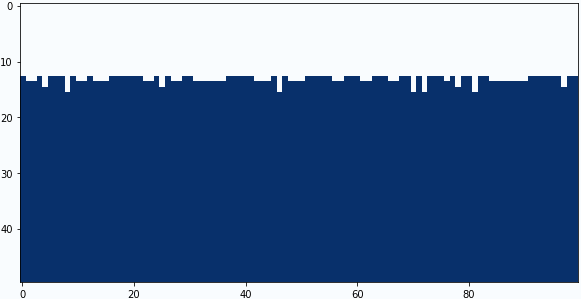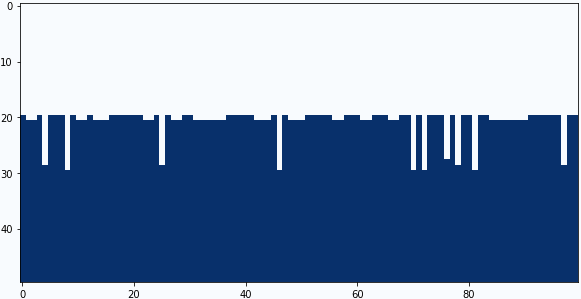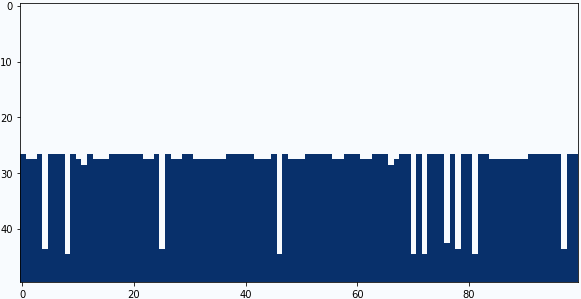
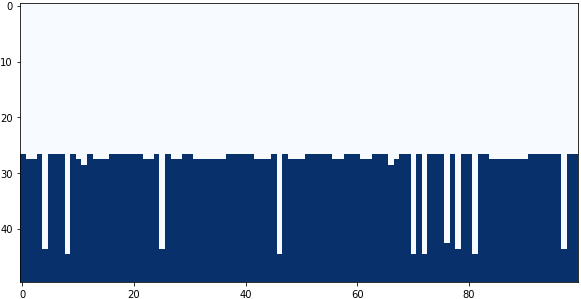
まとめ
結果の3番目くらいが私は好きですね。ごく簡単なモデルですが、南米アンデスのペニテンテを再現できたと思います。

