やること
ライフゲームには様々なバリエーションがあります。今回はHighLifeと呼ばれるルールを試してみましょう。
参考文献
HighLifeについてはWikipediaを、
http://www.conwaylife.com/wiki/HighLife
変則ルールについてはこちらの動画も魅力的にまとまっています。
もうひとつのライフゲーム Life-like cellular automata
もうひとつのライフゲーム Life-like cellular automata ライフゲームのバリエーション HighLife, Replicator, Day & Night, 2x2 の紹介です...
基本ルールと変則ルール
17-1で用いた基本ルールはこちらで、この条件に当てはまらない場合は死となります。
| 次のステップでの生存条件 | |
| 生存セル | 隣接する8セルのうち生存セルが2、3個 |
| 死セル | 隣接する8セルのうち生存セルが3個 |
このルールを23/3と表現したとき、他に23/36ルールや34/34ルールといった変則ルールが有名なようです。
23/36ルール(HighLifeとも呼ばれる)
| 次のステップでの生存条件 | |
| 生存セル | 隣接する8セルのうち生存セルが2、3個 |
| 死セル | 隣接する8セルのうち生存セルが3、6個 |
34/34ルール
| 次のステップでの生存条件 | |
| 生存セル | 隣接する8セルのうち生存セルが3、4個 |
| 死セル | 隣接する8セルのうち生存セルが3、4個 |
34678/3678ルール(Day and Nightとも呼ばれる)
| 次のステップでの生存条件 | |
| 生存セル | 隣接する8セルのうち生存セルが3、4、6、7、8個 |
| 死セル | 隣接する8セルのうち生存セルが3、6、7、8個 |
実行環境
どちらかを用いますが、WinPythonをおすすめします。WinPythonでは図が紙芝居のようにパラパラ流れて見やすいですが、Colabではスクロールする必要があり見づらいです。
Colabにも対応しました!(推奨)
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
Google Colaboratoryが利用可能です。

Google Colab
ソースコード
基本的には17-1の記事のソースコードに、死んだセルの誕生条件を1行書き加えただけです。初期状態の設定も今回のテーマに合わせて書き換えています。
↓WinPythonコード
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 81, 81
#任意の状態を用意
state = np.array([[1,1,1,0,0],
[1,0,0,1,0],
[1,0,0,0,1],
[0,1,0,0,1],
[0,0,1,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (38, 38)
#終了ステップ数
max_step = 200
#============================
#メイン処理
#============================
#フィールドの生成
f = np.zeros((h, w), dtype=bool)
#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state
#初期状態の表示
plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='inferno')
#plt.savefig('save/{}.png'.format(0), bbox_inches='tight', pad_inches=0)
plt.show(), print()
#状態の更新
for i in range(1, max_step + 1):
#周囲の生存マス数を記録するための配列
mask = np.zeros((h, w))
#周囲の生存マスを足し込む
mask[1:, :] += f[:-1, :] #上
mask[:-1, :] += f[1:, :] #下
mask[:, 1:] += f[:, :-1] #左
mask[:, :-1] += f[:, 1:] #右
mask[1:, 1:] += f[:-1, :-1] #左上
mask[1:, :-1] += f[:-1, 1:] #右上
mask[:-1, 1:] += f[1:, :-1] #左下
mask[:-1, :-1] += f[1:, 1:] #右下
#未来のフィールド(すべて死状態)
future = np.zeros((h, w), dtype=bool)
#生きているマスが生きる条件(=生存)
future[mask*f==2] = 1
future[mask*f==3] = 1
#死んでいるマスが生きる条件(=誕生)
future[mask*~f==3] = 1
future[mask*~f==6] = 1 #ここ追加しましたよ
#フィールドの更新(浅いコピーに注意)
f = future
#表示
plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='inferno')
#plt.savefig('save/{}.png'.format(i), bbox_inches='tight', pad_inches=0)
plt.show(), print()↓Colabコード
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from matplotlib import animation, rc
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 81, 81
#任意の状態を用意
state = np.array([[1,1,1,0,0],
[1,0,0,1,0],
[1,0,0,0,1],
[0,1,0,0,1],
[0,0,1,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (38, 38)
#終了ステップ数
max_step = 200
#============================
#メイン処理
#============================
#フィールドの生成
f = np.zeros((h, w), dtype=bool)
#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state
#画像をスタックする配列の準備
fig = plt.figure()
#fig = plt.figure(figsize=(10, 10))
ims = []
#初期状態の表示(スタック)
im = plt.imshow(f, cmap='inferno')
ims.append([im])
#状態の更新
for i in range(1, max_step + 1):
#周囲の生存マス数を記録するための配列
mask = np.zeros((h, w))
#周囲の生存マスを足し込む
mask[1:, :] += f[:-1, :] #上
mask[:-1, :] += f[1:, :] #下
mask[:, 1:] += f[:, :-1] #左
mask[:, :-1] += f[:, 1:] #右
mask[1:, 1:] += f[:-1, :-1] #左上
mask[1:, :-1] += f[:-1, 1:] #右上
mask[:-1, 1:] += f[1:, :-1] #左下
mask[:-1, :-1] += f[1:, 1:] #右下
#未来のフィールド(すべて死状態)
future = np.zeros((h, w), dtype=bool)
#生きているマスが生きる条件(=生存)
future[mask*f==2] = 1
future[mask*f==3] = 1
#死んでいるマスが生きる条件(=誕生)
future[mask*~f==3] = 1
future[mask*~f==6] = 1 #ここ追加しましたよ
#フィールドの更新(浅いコピーに注意)
f = future
#表示
#表示(スタック)
im = plt.imshow(f, cmap='inferno')
ims.append([im])
#アニメーション表示の準備
print('making animation......')
print('len(ims) = ' + str(len(ims)))
ani = animation.ArtistAnimation(fig, ims, interval=50, blit=True)
#ここにアニメを表示する場合はこちらを有効に
rc('animation', html='jshtml')
ani
#.gifや.mp4を保存する場合はこちらを有効に
#ani.save('aaa.gif', writer='imagemagick',fps=40)
#ani.save('bbb.mp4', writer="ffmpeg")自己複製を実行してみる
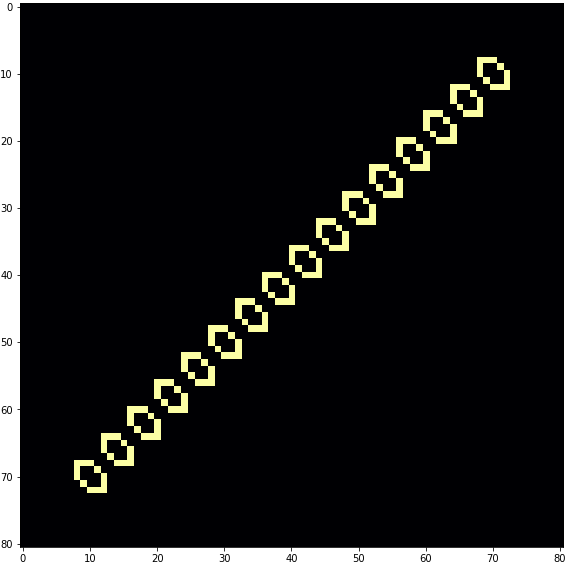
ソースコードをそのまま実行すると、細胞のような物体が1→2→4→8個と自己複製し始めます。
まとめ
同様に他の変則ルールにも挑戦してみたいですね。実装できたらぜひSlackで報告してください!または、Twitterでこの記事のURLを添付してつぶやいていただけたら嬉しいです。

