やること
ライフゲームのプログラムを改造して、チューリング・パターンを作ってみます。
参考文献
反応拡散方程式のGray-Scottモデルについては、sakamotoさんの記事をご参照ください。
非線形科学 : monman53
こちらの2つのシミュレータが楽しいです。
WebGL Gray-Scott Explorer at MROB
Reaction diffusion simulation
拡散項と反応項
こちらが Gray-Scottモデルです。
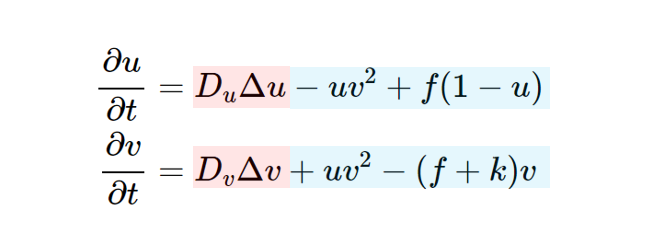
物質u, vがあり、Du, Dvは拡散係数、f, kはパラメータです。これをごにょごにょすると、各セルを更新するための式(du/dt, dv/dt)が得られます。
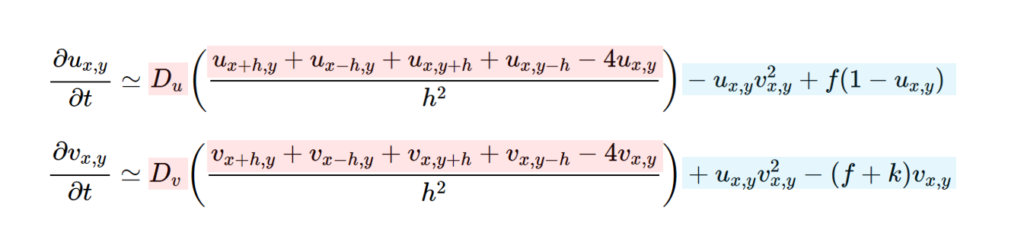
赤い部分が拡散項です。簡単のために、セル間の距離hは1として無視します。拡散項は、各セルが周りのセルからどのような影響を受けるかを表していて、
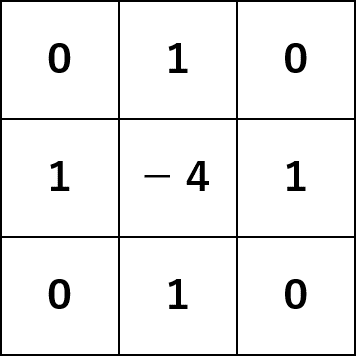
自身を中央としてこのような重み付けで足し込んでくださいという意味です。
青い部分は反応項です。これは各セルのu, vとパラメータf, kを使って計算できます。
実行環境
WinPythonかGoogle Colaboratoryを用います。
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
Google Colaboratoryが利用可能です。

Google Colab
ソースコード
ライフゲームのときは用いませんでしたが、scipy.signal.convolve2d()を用いると、4近傍や8近傍の足し込みが1行でできます。
↓WinPythonコード
import numpy as np
import numpy.random as nr
from scipy import signal
import matplotlib.pyplot as plt
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 100, 100
#終了ステップ数
max_step = 10000
#拡散係数
D1 = 0.2
D2 = 0.1
#キリン模様
start = 1 #0:中央のみ、1:複数
f = 0.082
k = 0.059
#伸びる線
#start = 1 #0:中央のみ、1:複数
#f = 0.058
#k = 0.065
#線の生成
#start = 0 #0:中央のみ、1:複数
#f = 0.046
#k = 0.063
#線といくらの生成
#start = 0 #0:中央のみ、1:複数
#f = 0.034
#k = 0.0618
#いくらウロウロ
#start = 1 #0:中央のみ、1:複数
#f = 0.014
#k = 0.054
#タピオカカオス
#start = 1 #0:中央のみ、1:複数
#f = 0.0353
#k = 0.0566
#細胞分裂
#start = 0 #0:中央のみ、1:複数
#f = 0.030
#k = 0.063
#細胞分裂パルス
#start = 0 #0:中央のみ、1:複数
#f = 0.022
#k = 0.059
#波(BZ反応)
#start = 1 #0:中央のみ、1:複数
#f = 0.0159
#k = 0.045
#============================
#メイン処理
#============================
#フィールドの初期化
u = np.ones((h, w))
v = np.zeros((h, w))
#初期状態の設定
size = 6
if start == 0:
#中央に乱数の正方形
u[h//2-size//2:h//2+size//2, w//2-size//2:w//2+size//2] = nr.rand(size, size)
v[h//2-size//2:h//2+size//2, w//2-size//2:w//2+size//2] = nr.rand(size, size)
if start == 1:
#ランダムな位置に複数の乱数正方形
for i in range(20):
p = (nr.randint(size, h-size), nr.randint(size, w-size))
u[p[0]-size//2:p[0]+size//2, p[1]-size//2:p[1]+size//2] = nr.rand(size, size)
v[p[0]-size//2:p[0]+size//2, p[1]-size//2:p[1]+size//2] = nr.rand(size, size)
#畳み込み用のフィルタ
g = np.array([[0.00, 1.00, 0.00],
[1.00, -4.0, 1.00],
[0.00, 1.00, 0.00]])
#表示
plt.figure(figsize=(10, 10))
plt.imshow(u, cmap='pink', vmin=0, vmax=1)
plt.savefig('save/{}.png'.format(0), bbox_inches='tight', pad_inches=0)
plt.show(), print()
#状態の更新
for i in range(1, max_step + 1):
#拡散項(u, vを畳み込んでdu, dvとする)
du = signal.convolve2d(u, g, mode='same',boundary='wrap') * D1
dv = signal.convolve2d(v, g, mode='same',boundary='wrap') * D2
#du, dvに反応項を加える
du = du - (u * v*v) + f*(1.0 - u)
dv = dv + (u * v*v) - (f + k)*v
#フィールドの更新(オイラー法)
u += du
v += dv
#表示
if i % 100 == 0:
plt.figure(figsize=(10, 10))
plt.imshow(u, cmap='pink', vmin=0, vmax=1)
plt.savefig('save/{}.png'.format(i), bbox_inches='tight', pad_inches=0)
plt.show(), print()
↓Colabコード
import numpy as np
import numpy.random as nr
from scipy import signal
import matplotlib.pyplot as plt
from matplotlib import animation, rc
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 100, 100
#終了ステップ数
max_step = 10000
#拡散係数
D1 = 0.2
D2 = 0.1
#キリン模様
start = 1 #0:中央のみ、1:複数
f = 0.082
k = 0.059
#伸びる線
#start = 1 #0:中央のみ、1:複数
#f = 0.058
#k = 0.065
#線の生成
#start = 0 #0:中央のみ、1:複数
#f = 0.046
#k = 0.063
#線といくらの生成
#start = 0 #0:中央のみ、1:複数
#f = 0.034
#k = 0.0618
#いくらウロウロ
#start = 1 #0:中央のみ、1:複数
#f = 0.014
#k = 0.054
#タピオカカオス
#start = 1 #0:中央のみ、1:複数
#f = 0.0353
#k = 0.0566
#細胞分裂
#start = 0 #0:中央のみ、1:複数
#f = 0.030
#k = 0.063
#細胞分裂パルス
#start = 0 #0:中央のみ、1:複数
#f = 0.022
#k = 0.059
#波(BZ反応)
#start = 1 #0:中央のみ、1:複数
#f = 0.0159
#k = 0.045
#============================
#メイン処理
#============================
#フィールドの初期化
u = np.ones((h, w))
v = np.zeros((h, w))
#初期状態の設定
size = 6
if start == 0:
#中央に乱数の正方形
u[h//2-size//2:w//2+size//2, h//2-size//2:w//2+size//2] = nr.rand(size, size)
v[h//2-size//2:w//2+size//2, h//2-size//2:w//2+size//2] = nr.rand(size, size)
if start == 1:
#ランダムな位置に複数の乱数正方形
for i in range(20):
p = (nr.randint(size, h-size), nr.randint(size, w-size))
u[p[0]-size//2:p[0]+size//2, p[1]-size//2:p[1]+size//2] = nr.rand(size, size)
v[p[0]-size//2:p[0]+size//2, p[1]-size//2:p[1]+size//2] = nr.rand(size, size)
#畳み込み用のフィルタ
g = np.array([[0.00, 1.00, 0.00],
[1.00, -4.0, 1.00],
[0.00, 1.00, 0.00]])
#画像をスタックする配列の準備
fig = plt.figure()
#fig = plt.figure(figsize=(10, 10))
ims = []
#初期状態の表示(スタック)
im = plt.imshow(u, cmap='pink', vmin=0, vmax=1)
ims.append([im])
#状態の更新
for i in range(1, max_step + 1):
#拡散項(u, vを畳み込んでdu, dvとする)
du = signal.convolve2d(u, g, mode='same',boundary='wrap') * D1
dv = signal.convolve2d(v, g, mode='same',boundary='wrap') * D2
#du, dvに反応項を加える
du = du - (u * v*v) + f*(1.0 - u)
dv = dv + (u * v*v) - (f + k)*v
#フィールドの更新(オイラー法)
u += du
v += dv
#表示(スタック)
if i % 100 == 0:
im = plt.imshow(u, cmap='pink', vmin=0, vmax=1)
ims.append([im])
#アニメーション表示の準備
print('making animation......')
print('len(ims) = ' + str(len(ims)))
ani = animation.ArtistAnimation(fig, ims, interval=50, blit=True)
#ここにアニメを表示する場合はこちらを有効に
rc('animation', html='jshtml')
ani
#.gifや.mp4を保存する場合はこちらを有効に
#ani.save('aaa.gif', writer='imagemagick',fps=40)
#ani.save('bbb.mp4', writer="ffmpeg")キリン模様
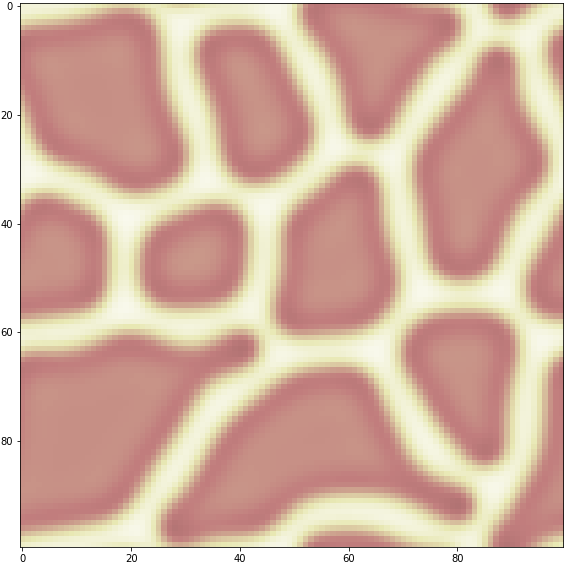
伸びる線
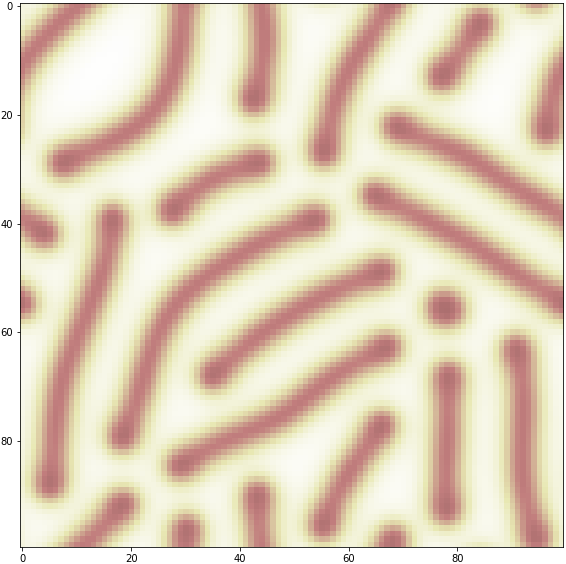
線の生成
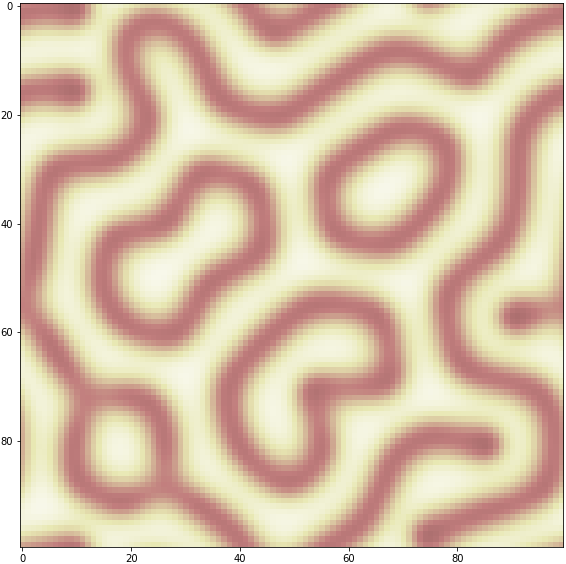
線といくらの生成
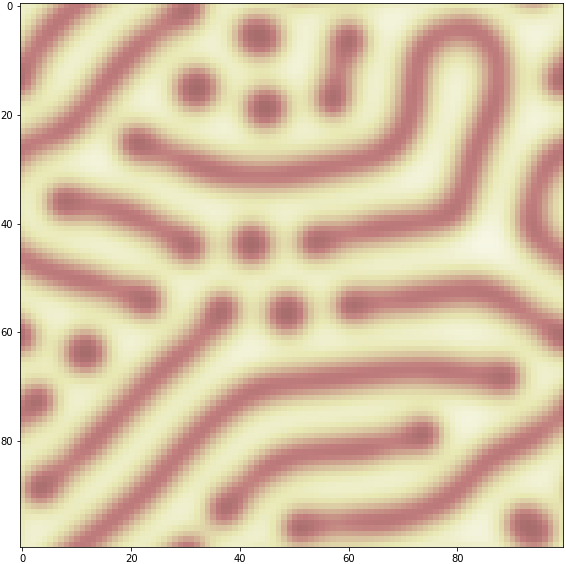
いくらウロウロ
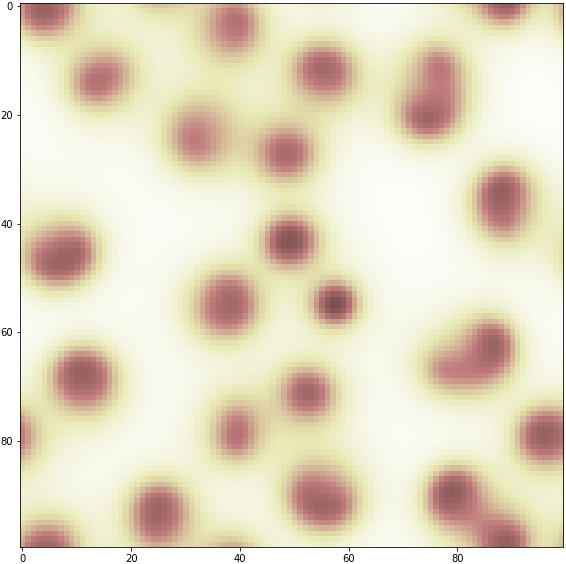
タピオカカオス
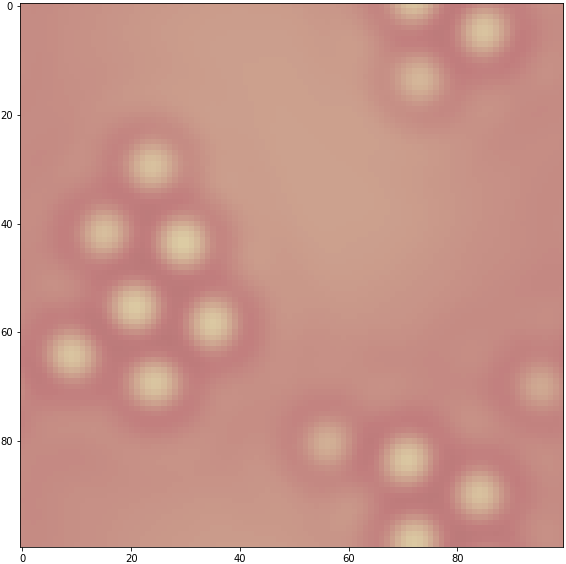
細胞分裂
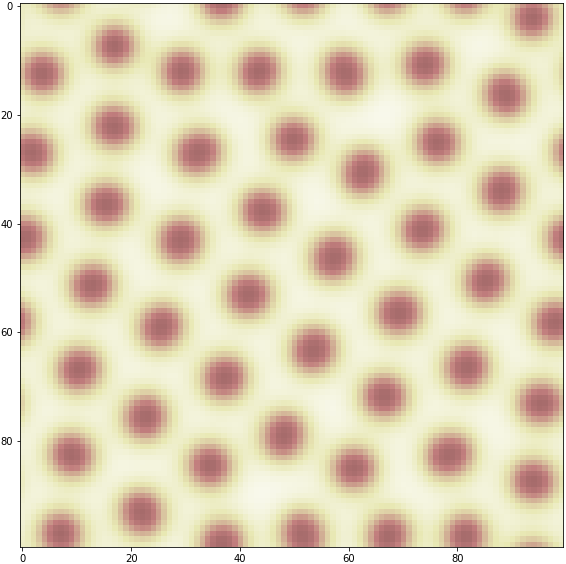
細胞分裂パルス
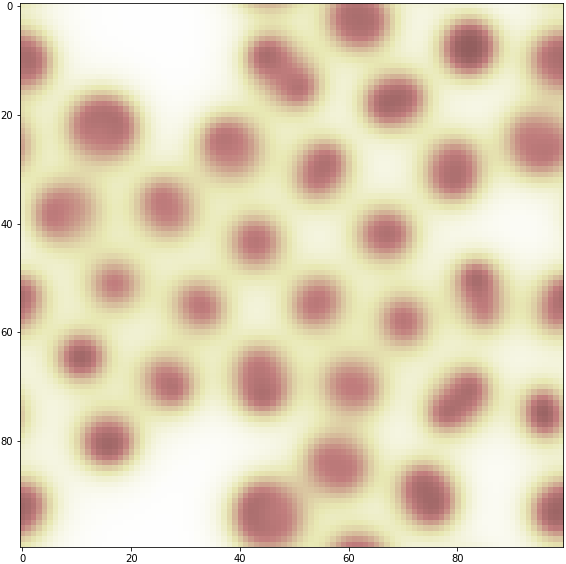
波(BZ反応)
余談ですが、BZ反応でこの渦を作るにはちょっとコツが要ります。
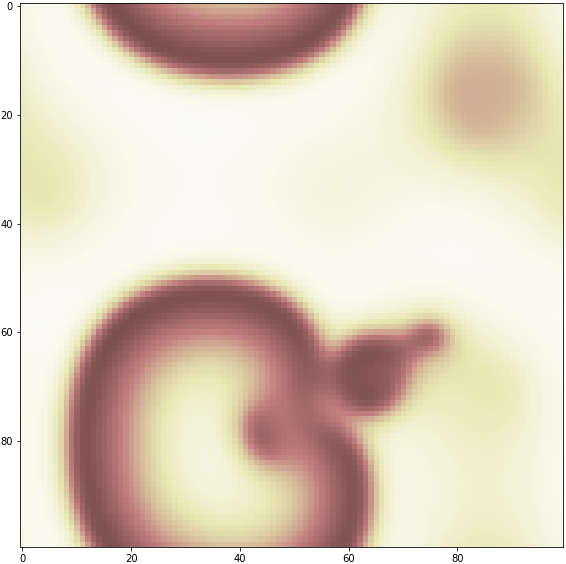
まとめ
非常に楽しい。参考文献のサイトには他のパラメータセットもありますので、ぜひ試してみてください。実装できたらぜひSlackで報告してください!または、Twitterでこの記事のURLを添付してつぶやいていただけたら嬉しいです。

