4/14(日)　足・靴・木型研究会「第2回研究集会」を開催します☆彡

21-18. 量子アニーリング（QUBO）で連立方程式を解いてみた

やること

誰かが言いました。

連立方程式は組合せ最適化問題である [要出典]

言ってないんだよなぁ。

今回はQUBOで連立方程式（文字が3つあるやつ）を解いてみます。

考え方

基本の条件設定「ｎ個の量子ビットからｍ個を１にする」から考えていきます。

例えば、「３個の量子ビットから２個を１にする」は次の式です。

H = (q0 + q1 + q2 - 2)**2

これはつまり、３個の量子ビットを足した値が２になるということです。それぞれの量子ビットは [0, 1] のどちらかを取ります。合計値が２であればエネルギーは最小で、合計値が２からずれるとエネルギーが高くなります。

ここで、量子ビット名を [x, y, z] に変えて、それぞれに係数 [5, -1, 2] をかけてみます。

H = (5*x - y + 2*z - 7)**2

実はこれで方程式「5x – y + 2z = 7」が完成しました。「5x – y + 2z」の部分が7のときにエネルギーは最小で、7からずれるとエネルギーが高くなります。

このような方程式を複数設定します。エネルギーが最小の量子ビットの状態を求めるということは、すなわち連立方程式を解くということです。数学の問題ではピッタリの解が存在するはずなので、アニーリングでは理論上の最小エネルギーの解が得られるはずです。

その他の設定可能な条件式も気になる方は過去のまとめ記事をご参照ください↓（宣伝）

21-12. 量子アニーリングのQUBOで設定可能な条件式まとめ（保存版）
やること2023/5/20追記：応用A4を追加2023/5/23追記：応用Dを追加 量子アニーリングで設定可能な条件式（QUBOで表現可能な条件）をまとめました。何度も参照するので私...
vigne-cla.com
2023/05/01

解が 0, 1 だけの場合

次の3元連立1次方程式を解きます。

(1)   \begin{equation*} \left\{ \begin{array}{lll} 5x - y +2z &= 7 \\ -3x +4y + z &= -2 \\ x -2y -4z &= -3 \right. \end{array} \end{equation*}

    $$ x, y, z = 1, 0, 1 $$

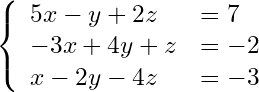
解が０または１であることが分かっていることを前提とします。解が０と１だけなので [x, y, z] をそのまま量子ビットで表せます。

from pyqubo import Binary
from dwave_qbsolv import QBSolv

#量子ビットを用意する
x = Binary('x')
y = Binary('y')
z = Binary('z')

#連立方程式の設定
H = 0
H += ( 5*x -  y +2*z - 7)**2
H += (-3*x +4*y +  z + 2)**2
H += (   x -2*y -4*z + 3)**2

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')

#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
offset
62.0
response
Sample:[1, 0, 1] Energy:-62.0 Occurrence:501

解が [1, 0, 1] と出ました。オフセットと解のエネルギーに着目すると、マイナスオフセットが理論上の最小エネルギーで、それに一致するエネルギーの解が得られています。この解は３つの方程式を完全に満たしていることを意味しています。

解が 0, 1, 2, 3 だけの場合

次の3元連立1次方程式を解きます。

(2)   \begin{equation*} \left\{ \begin{array}{lll} x + y + z &= 6 \\ 2x +3y -2z &= 11 \\ 3x - y + z &= 4 \right. \end{array} \end{equation*}

    $$ x, y, z = 2, 3, 1 $$

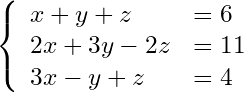
解が０～３の整数であることが分かっていることを前提とします。この場合、[x, y, z] をそのまま量子ビットで表すことができません。そこで [x0, x1] という量子ビットを用意して、「x = 2*x0 + x1」のように２進数表現（2bit）します。x0が2^1の桁、x1が2^0の桁です。

from pyqubo import Binary
from dwave_qbsolv import QBSolv

#量子ビットを用意する
x0 = Binary('x0')
x1 = Binary('x1')

y0 = Binary('y0')
y1 = Binary('y1')

z0 = Binary('z0')
z1 = Binary('z1')

#x,y,zを2進数（2bit）で表す
x = 2*x0 + x1
y = 2*y0 + y1
z = 2*z0 + z1

#連立方程式の設定
H = 0
H += (  x +  y +  z -  6)**2
H += (2*x +3*y -2*z - 11)**2
H += (3*x -  y +  z -  4)**2

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')

#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=500)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
    
    #2進数から戻して確認
    x0, x1 = list(sample.values())[:2]
    y0, y1 = list(sample.values())[2:4]
    z0, z1 = list(sample.values())[4:]
    print(f'x = {2*x0 + x1}')
    print(f'y = {2*y0 + y1}')
    print(f'z = {2*z0 + z1}')

offset
173.0
response
Sample:[1, 0, 1, 1, 0, 1] Energy:-173.0 Occurrence:501
x = 2
y = 3
z = 1

正しい解が得られました！

解が 0～255 の整数の場合

最後に、次の3元連立1次方程式にチャレンジします。

(3)   \begin{equation*} \left\{ \begin{array}{lll} 10x +14y +4z &= 5120 \\ 9x +12y +2z &= 4230 \\ 7x + 5y +2z &= 2360 \right. \end{array} \end{equation*}

    $$ x, y, z = 130, 230, 150 $$

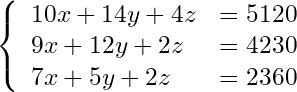
解が0～255の整数であることが分かっていることを前提とします。お察しの通り、[x0, x1, x2, x3, x4, x5, x6, x7] という量子ビットを用意して、「x = 128*x0 + 64*x1 + 32*x2 + 16*x3 + 8*x4 + 4*x5 + 2*x6 + x7」という２進数表現（8bit）をします。3元の連立方程式に24量子ビットを使います。

from pyqubo import Binary
from dwave_qbsolv import QBSolv

#量子ビットを用意する
x0 = Binary('x0')
x1 = Binary('x1')
x2 = Binary('x2')
x3 = Binary('x3')
x4 = Binary('x4')
x5 = Binary('x5')
x6 = Binary('x6')
x7 = Binary('x7')

y0 = Binary('y0')
y1 = Binary('y1')
y2 = Binary('y2')
y3 = Binary('y3')
y4 = Binary('y4')
y5 = Binary('y5')
y6 = Binary('y6')
y7 = Binary('y7')

z0 = Binary('z0')
z1 = Binary('z1')
z2 = Binary('z2')
z3 = Binary('z3')
z4 = Binary('z4')
z5 = Binary('z5')
z6 = Binary('z6')
z7 = Binary('z7')

#x,y,zを2進数（8bit）で表す
x = 128*x0 + 64*x1 + 32*x2 + 16*x3 + 8*x4 + 4*x5 + 2*x6 + x7
y = 128*y0 + 64*y1 + 32*y2 + 16*y3 + 8*y4 + 4*y5 + 2*y6 + y7
z = 128*z0 + 64*z1 + 32*z2 + 16*z3 + 8*z4 + 4*z5 + 2*z6 + z7

#連立方程式の設定
H = 0
H += (10*x +14*y +4*z - 5120)**2
H += ( 9*x +12*y +2*z - 4230)**2
H += ( 7*x + 5*y +2*z - 2360)**2

#コンパイル
model = H.compile()
qubo, offset = model.to_qubo()
print(f'offset\n{offset}')

#分割サンプリング
response = QBSolv().sample_qubo(qubo, num_repeats=1000)

#レスポンスの確認
print('response')
for (sample, energy, occurrence) in response.data():
    print(f'Sample:{list(sample.values())} Energy:{energy} Occurrence:{occurrence}')
    
    #2進数から戻して確認
    x0,x1,x2,x3,x4,x5,x6,x7 = list(sample.values())[:8]
    y0,y1,y2,y3,y4,y5,y6,y7 = list(sample.values())[8:16]
    z0,z1,z2,z3,z4,z5,z6,z7 = list(sample.values())[16:]
    print(f'x = {128*x0+64*x1+32*x2+16*x3+8*x4+4*x5+2*x6+x7}')
    print(f'y = {128*y0+64*y1+32*y2+16*y3+8*y4+4*y5+2*y6+y7}')
    print(f'z = {128*z0+64*z1+32*z2+16*z3+8*z4+4*z5+2*z6+z7}')
offset
49676900.0
response
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0] Energy:-49676900.0 Occurrence:9
x = 130
y = 230
z = 150
Sample:[1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0] Energy:-49676871.0 Occurrence:9
x = 130
y = 229
z = 154
Sample:[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0] Energy:-49676814.0 Occurrence:9
x = 127
y = 232
z = 152

サンプリング数を1000に増やしていますが、何回も実行してたまたま正解が出たときの結果を載せています。一応ちゃんと解けましたね！

さいごに

最後のは正解が得られる確率が低かったです。これはアニーリングアルゴリズム（アニーリングマシン）の性能によるところでしょうか。神様が理想的なアニーリングマシンを用意してくれたら、ただの１回のアニーリングで最適解が得られるはずなのですが。

タイトルとURLをコピーしました