はじめに
t検定が分からないという声があったのでダーツで説明してみたいと思います。「母集団」「標本」「P値」あたりのイメージ把握にどうぞ。後半に悪用テクニックも載せたので皆さんも活用してお金を稼いでください。
t検定はガチで奥が深いので、どなたか詳しい方の修正や寄稿をお待ちしておりますm(_ _)m
予習
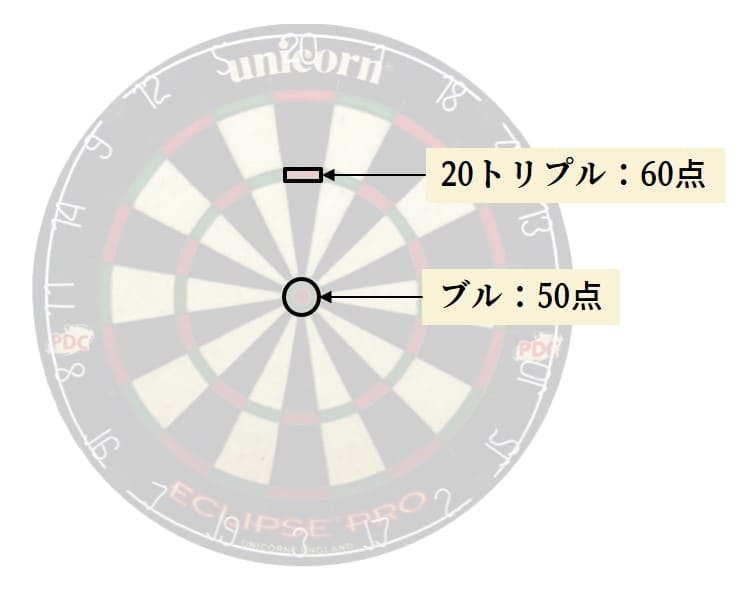
ダーツを知らない方のために、真ん中をブル(50点)、20点ゾーンの中の細いところが20点のトリプルで60点です。
ダーツをしよう
AさんとBさんはダーツで遊ぶことにしました。
Aさんは言いました。「10回ずつ投げて合計得点が高いほうが勝ちね」
2人の投げた結果は次のとおりでした。
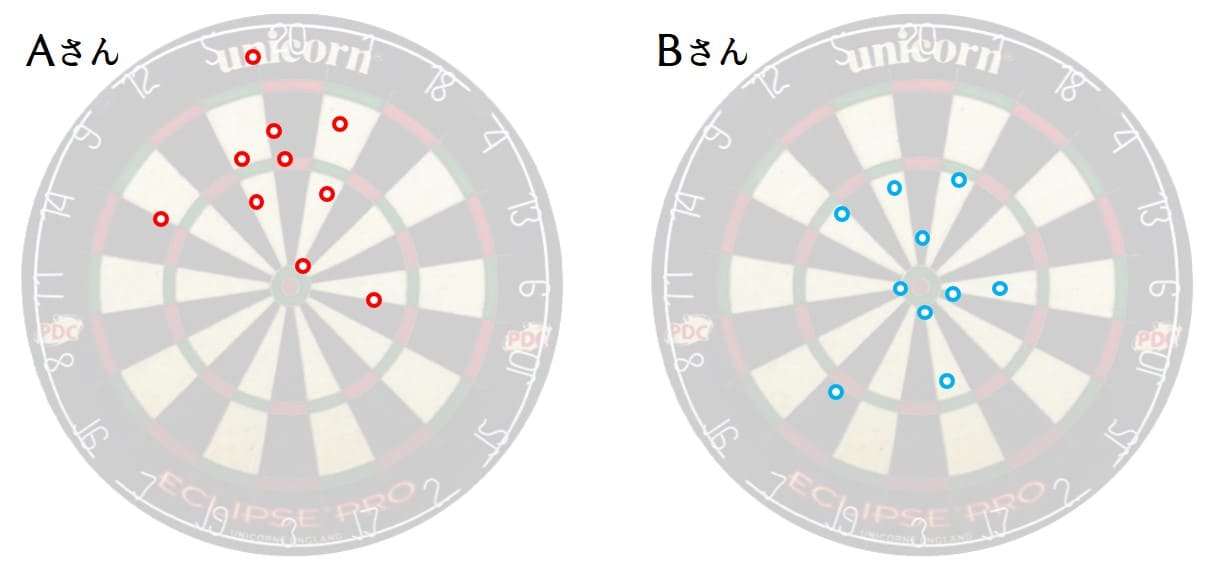
これを見てAさんは言いました。「あれ?お前ちゃんと最高得点のところ狙ってる?」
Bさん「ちゃんと狙ったよ!え??」
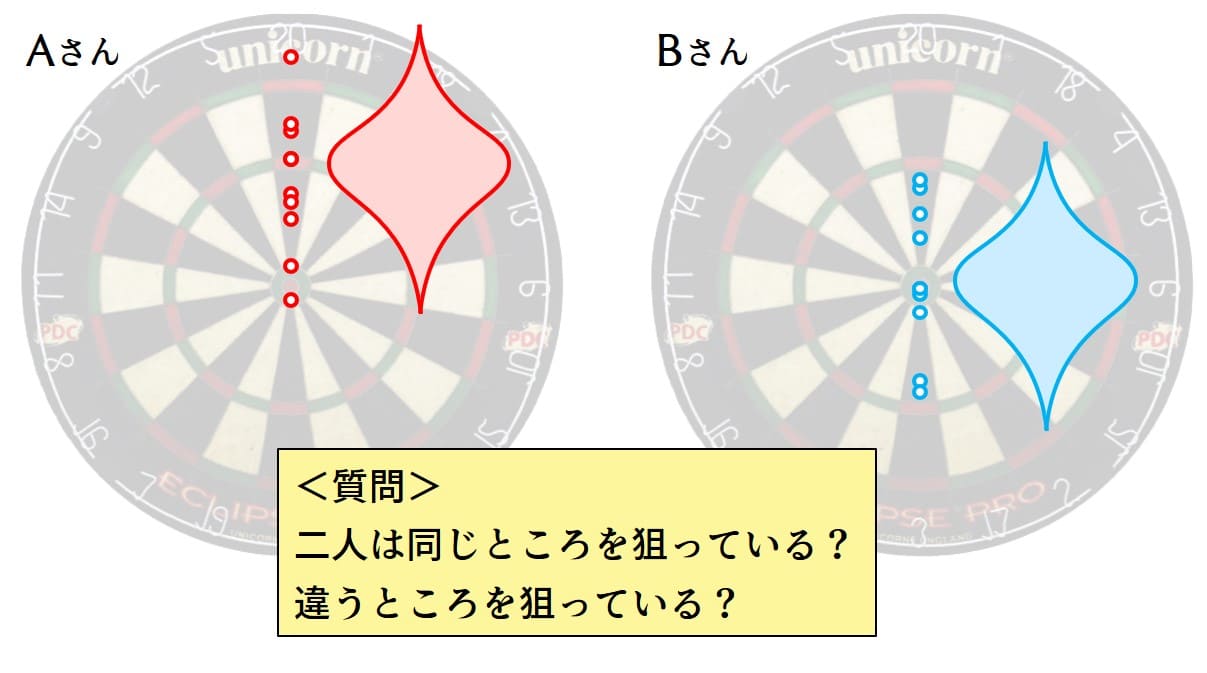
簡単のために矢を真ん中に寄せてみます。さて、2人は同じ場所を狙っていると言えるでしょうか?
母集団の分布は神様にしか見えない
2人は同じ場所を狙っていると言えるか?
これを確かめるために神様になって時間を巻き戻し、2人に無限回投げさせてみました。
このようになりました。
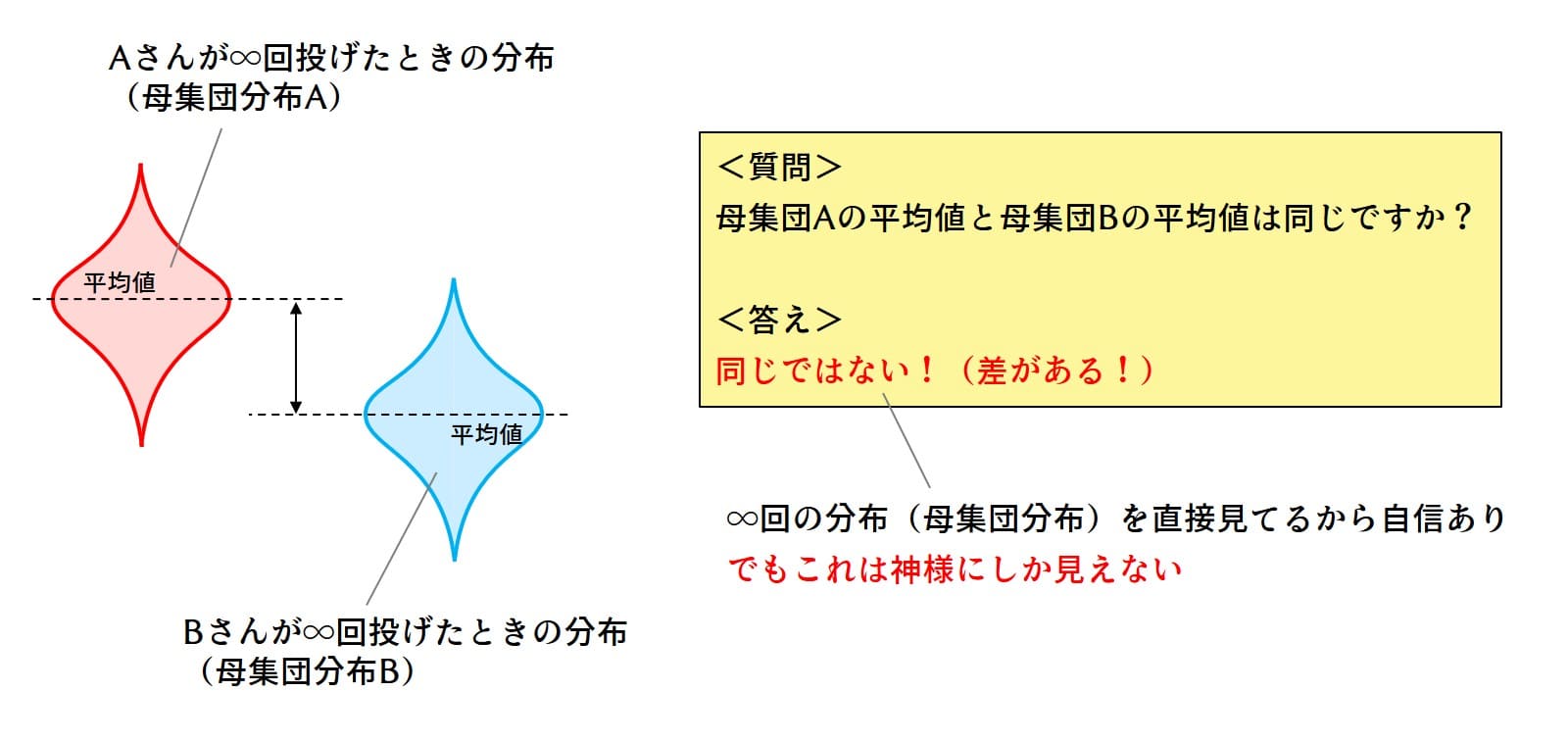
2人の結果はきれいに正規分布していて平均値が確かに違います。したがって2人が狙った場所(母集団の平均値)は違う、ということが分かります。
しかしこれは神様の視点。実際には10回ずつしか投げていないのです。
標本の分布から母集団の分布は分からない
実際には10回ずつしか投げていません(大事なことなので2回言いm)
平均値には多少の差があるようですが、これは狙った場所が違ったことによる差なのか、それとも同じ場所を狙ったけどたまたまこれくらいの差になったのか、分かりません。

助けてドラえもーーーーん!!
てってれてってってーーーー!!
t検定 ლ( ͡° ͜ʖ ͡° ლ)
t検定をしよう
t検定の手順は次のとおりです。
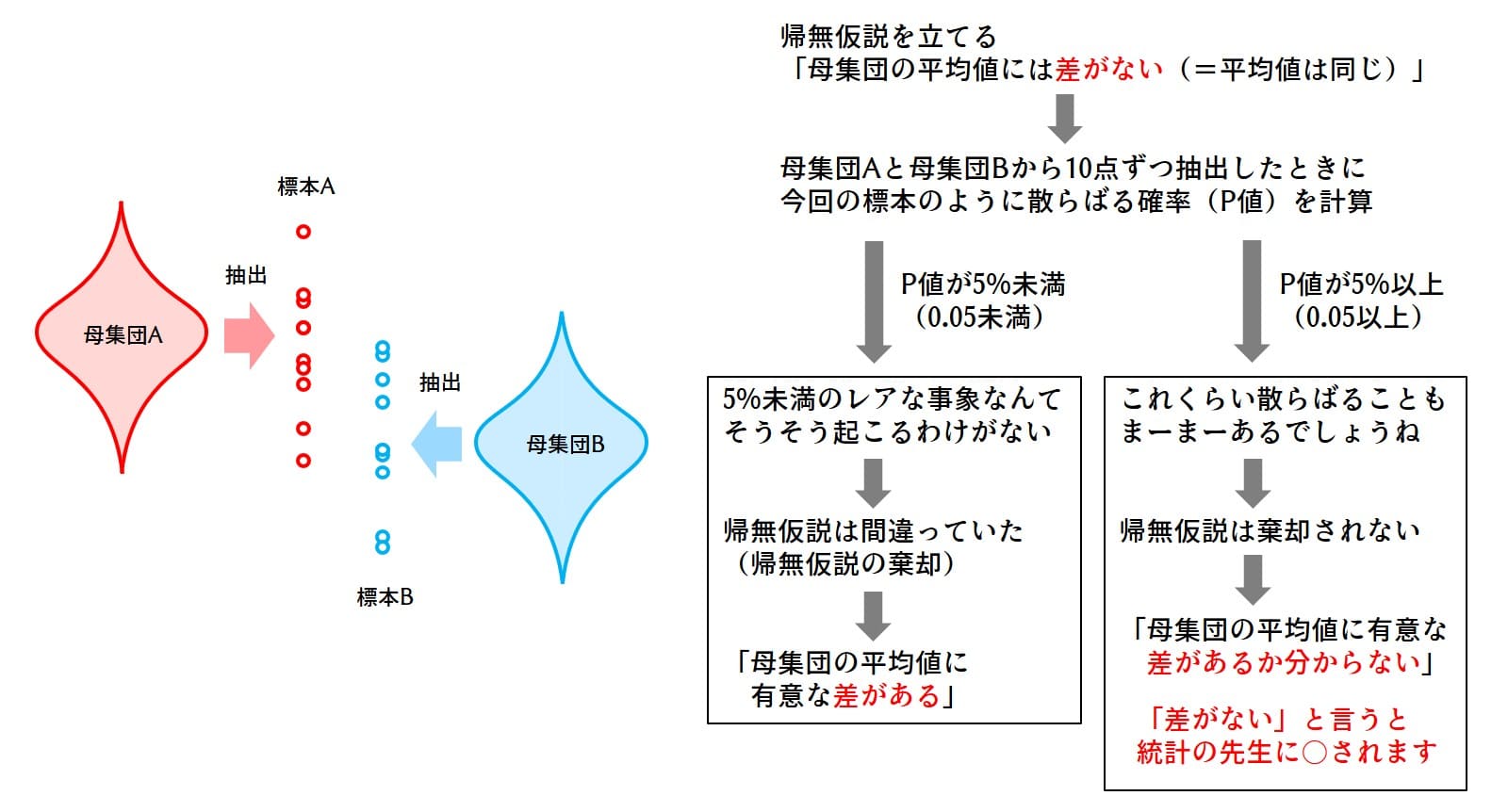
帰無仮説という言葉が難しいですが、やってることは背理法みたいな感じです。言いたいことと逆のことを仮定して、「それじゃおかしいですよね」→「仮定が間違っていた」→「言いたいことが言えた」という作戦です。
今回は「同じ場所を狙ったけどたまたまこれくらいの差になる」確率を計算します。これをP値と呼びます。
P値が0.05未満
P値が0.05未満であれば、「同じ場所を狙ったけどたまたまこれくらいの差になる」ことは5%未満の非常にレアな事象です。SSR 5%のガチャが1回で当たりますか?当たらないですよね。だから「同じ場所を狙った」は間違っていて、「違う場所を狙った」と主張することができます。
P値が0.05以上
一方、P値が0.05以上であれば、「同じ場所を狙ったけどたまたまこれくらいの差になる」ことは5%以上の確率で起こるありふれた事象です。まあ同じ場所を狙ってもこれくらい差が出ることもあるよな?って感じです。よって何も分かりません。

※注意:P値が0.05以上だからといって「(母集団の平均値に)差がない」とは言えません。うっかり言っちゃうと統計の先生にシバき倒されます。
t検定の結果
今回、t検定をしてみるとP値は0.04でした。
「同じ場所を狙ったにしてはちょっと差がありすぎる」ってことで「狙った場所が違った」と主張することができます。
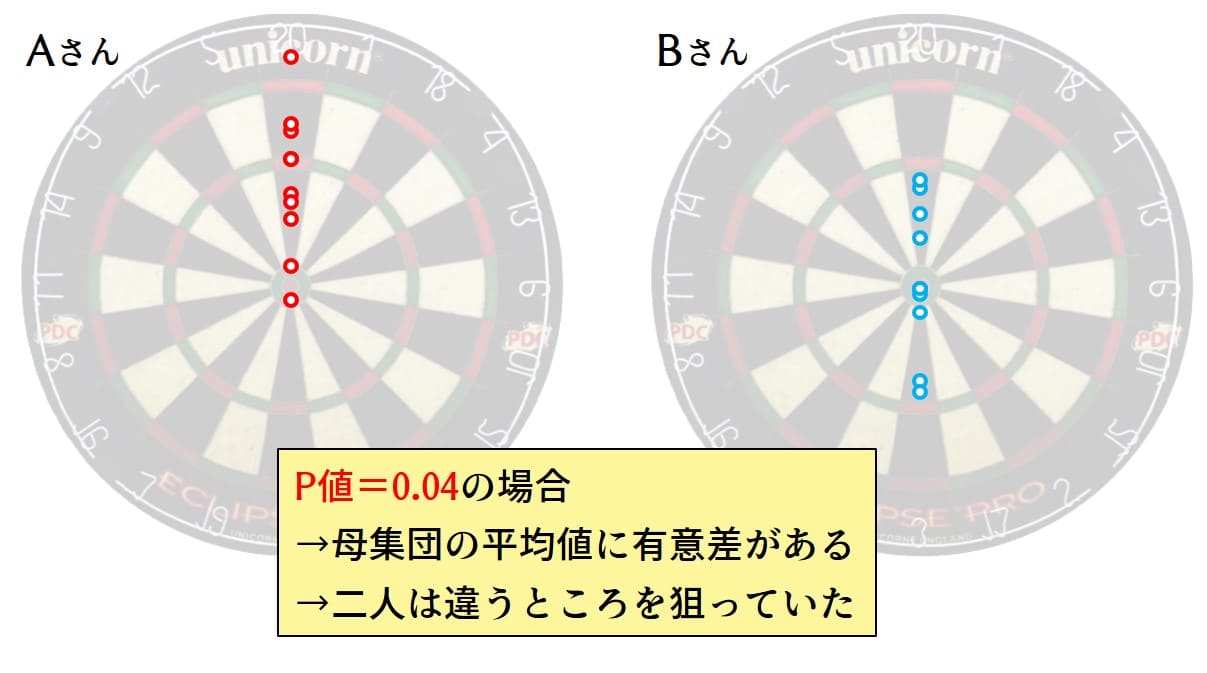
Bさん「え??真ん中が最高得点じゃないの!?知らなかったよ~」
めでたしめでたし♪
ところで、わざわざ「主張することができる」と言っているのはなぜでしょうか?「狙った場所が違った」と言い切れないのでしょうか?
言い切れません。母集団の分布は神様にしか見えないので、母集団がどうこうを断定することはできません。
しかしそれでは何も言えなくなって科学が発展しないので、偉い人たちは「P値が5%未満だったら母集団に差があるって言っちゃっていいことにしようぜ?聞いた人もそれを信じること!いいね!?」と決めて運用しているのです。
近年はこの運用方針を見直す運動も起きていて、「5%じゃ甘いから1%にしようぜ」という派閥が増えています。1%を標準とする論文誌もあるようです。
ただ、たとえP値のボーダーを1%にしたとしても、100個の世界線があって100回の実験と検定を行った場合、1回くらいは誤って「本当は母集団に差がないのに差があると言い切ってしまう」ことが起きてしまうのです。t検定はどこまで突き詰めても確率なので「まあ信じて議論を進めましょう」ってな感じで。
補足
t検定が使える条件
スチューデントのt検定:「母集団が正規分布(しかも分散が等しい)と仮定できる」場合
今回のダーツの場合、矢の散らばり具合は概ね正規分布で、かつ、2人の分散は同じだろうと仮定できそうなのでスチューデントのt検定が使えます。
ウェルチのt検定:「母集団が正規分布(ただし分散が違う)と仮定できる」場合
2人の技量に差があって、Aさんはまとまりが良い(グルーピングが良い)、Bさんは散らばる、こんな場合はウェルチのt検定になると思います。
「対応がある場合」「正規分布ではない場合」「片側だ両側だ」いろいろ検定の種類が分岐するようなので別途検索してください。
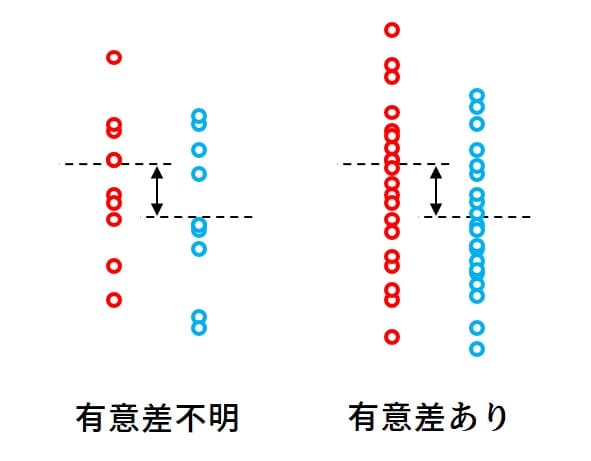
標本数は多ければいい
標本の平均値にどれくらいの差があれば「有意差あり」の判定になるか。同じ差であっても標本数が多いほど「有意差あり」と出やすいです(数式は検索)。小さな差であっても大量のサンプルによるものであれば信頼できる差と言えるわけです。
悪用テクニック
t検定は悪用できます。知識不足で意図せずに悪用してしまう人もいます。でもだいたいバレません。そこそこ倫理観が高い学術界でも問題になっているのですから、薄汚れた産業界なんてぜっっっっっっっっったいに悪用しています。広告代理店とか。何かの調査会社とか。そういうところが出しているプレスリリースとか。パンフレットとか。株式会社というのは株価を上げるためにはどんな手段も厭いません。だって民衆は馬鹿だから。バレなきゃ犯罪じゃn
悪用テクニック1
新発売のハンドクリームの効き目を確かめるため「20人 vs 20人で差が出るか」実験しました。t検定の結果、P値は0.06でした。惜しいなぁ。もう少しで5%未満だったんだけど。まあいいや。プレスリリースの棒グラフには「p<0.1で有意差を確認」と表記しよう。
え?じゃあp<0.07って書けば?
そうは書かないですよね?なぜ5%とか10%とかキリがいい数字が使われているか分かりますか?t検定は先に有意水準を決めてから行います。Pを見てから有意水準を変えるのは反則です。
悪用テクニック2
100種類の薬の候補を作りました。それぞれの候補薬について「マウス20匹 vs 20匹で差が出るか」実験しました。100回の実験をそれぞれ有意水準5%でt検定したところ、5種類の薬で有意差が出ました。この5つの薬は効能があると言えます。
言えますかね?
小麦粉でも水素水でも100世界線やれば5世界線くらいは有意差が出ます。
悪用テクニック3
ある薬の候補を作りました。「マウス20匹 vs 20匹で差が出るか」実験しました。有意差は出ませんでした。もう5匹追加して25匹 vs 25匹にしました。有意差は出ませんでした。もう5匹追加して30匹 vs 30匹にしました。ようやく有意差が出ました。よし論文を書こう。「マウス30匹 vs 30匹で実験したところ有意差が認められた」と。
◯んでください。
株価がたまたま上がった瞬間を切り取って「投資の必勝法」みたいな自慢をしないでください。
おわりに
同じようなノリの記事をもっと読みたいという方は以下もどうぞ。





