8-11. 遺伝的アルゴリズム（vcopt）で3-Deceptive問題を解く

やること
実行環境
3-Deceptive問題とは
パラメータ設定と評価関数
GAで解く
まとめ

やること

組合せ最適化にはいろいろなベンチマーク問題がありますが、3-Deceptive問題は変数間依存性のある騙し問題のひとつです。実装がとてもシンプルですのでGAで解いてみましょう。

実行環境

WinPython3.6をおすすめしています。

WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net

Portable Scientific Python 2/3 32/64bit Distribution for Windows

vcoptの使い方についてはチュートリアルをご参照ください。

vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。

3-Deceptive問題とは

長さ N（ただし N は３の倍数）の配列に対して、手前から３変数ずつをセットにしてスコアを付けていきます。もっともスコアが大きくなる配列を求める問題です。

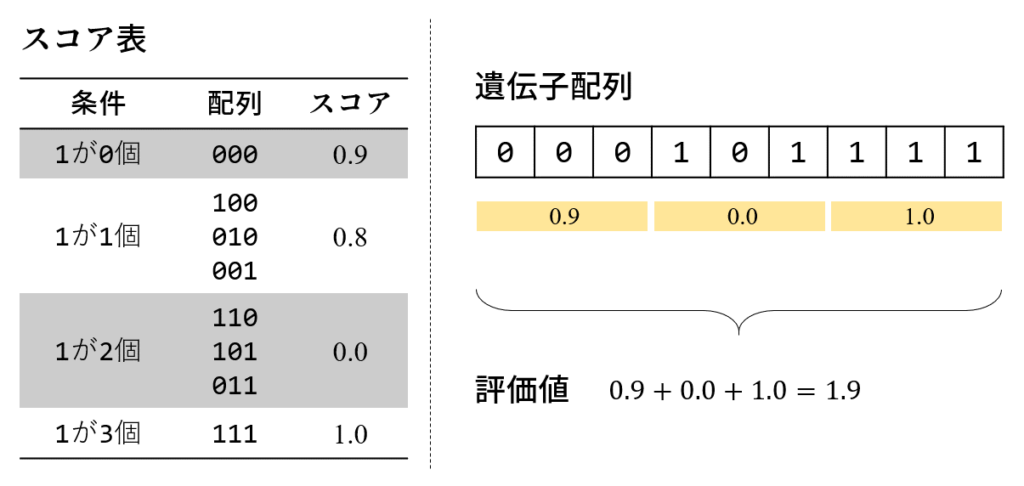
この問題の大域解は全部が１のときで、スコアは N /３です。これが「騙し問題」と呼ばれるのは、”000″のブロックが0.9点と非常に惜しいスコアを持ち、そこから”111″＝1.0点のブロックに移行する過程で”100″や”110″の低スコア領域を通らなければならないからです。”110″は配列としては最適に近いのに、スコアは最悪になってしまうのです。

また「変数間依存性がある」というのは、変数が３つずつセットで評価されるため、変数を個別に最適化することができないことを意味しています。自分一人だけが０から１に変わってもスコアは上がりにくいということです。

確認ですが、大域解は全ブロックが”111″のとき。想定される局所解は一部のブロックが”000″の状態です。

パラメータ設定と評価関数

vcoptをインストールします。

pip install vcopt

評価関数はシンプルです。

import numpy as np
import numpy.random as nr
from vcopt import vcopt

#=============================
# 3-Deceptive問題のパラメータ
#=============================
#パラメータ数
N = 30

#Nは3の倍数でなければならない
assert N % 3 == 0

#=============================
# 評価関数
#=============================
def Deceptive_score(para):
    #3個セットのブロックが並ぶように成形
    blocks = para.reshape(-1, 3)
    
    #スコア
    score = 0
    for block in blocks:
        if np.sum(block) == 0:
            score += 0.9
        if np.sum(block) == 1:
            score += 0.8
        if np.sum(block) == 2:
            score += 0.0
        if np.sum(block) == 3:
            score += 1.0
    
    #スコアを返す
    return score

#適当な遺伝子配列を生成して動作確認
para = nr.randint(0, 2, N)
print('para:\n{}'.format(para))
print('Deceptive_score(para):\n{}'.format(Deceptive_score(para)))

para:
[0 1 1 1 1 1 0 1 0]
Deceptive_score(para):
1.8

できました。

ちなみにPythonはfor文が遅いことで知られており、評価関数を以下のように書くと実行速度が約２倍になります。

#=============================
# 評価関数
#=============================
def Deceptive_score(para):
    #各ブロックの1の数の配列
    ones = np.sum(para.reshape(-1, 3), axis=1)
    
    #スコア配列
    scores = np.zeros(len(ones))
    scores[ones==0] = 0.9
    scores[ones==1] = 0.8
    scores[ones==3] = 1.0
    
    #合計値をスコアとして返す
    return np.sum(scores)

GAで解く

離散的なGAにあたるので vcopt().dcGA() を用います。

#=============================
# GAで最適化
#=============================
#para_range
para_range = np.array([[0, 1] for j in range(N)])
#GAの実行
para, score = vcopt().dcGA(para_range,              #選択肢の配列
                           Deceptive_score,         #評価関数
                           N//3,                    #評価値の目標値
                           show_pool_func='print')  #可視化オプション

________________________________________ info ________________________________________
para_range     : n=9
score_func     : <class 'function'>
aim            : ==3.0
show_pool_func : 'print'
seed           : 0
pool_num       : 90
max_gen        : None
core_num       : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 90/90        
gen=       0, best_score=   2.900, mean_score=   1.592, mean_gap=   1.408, time=   0.0
gen=      90, best_score=   2.900, mean_score=   2.191, mean_gap=   0.809, time=   0.0
gen=     180, best_score=   2.900, mean_score=   2.454, mean_gap=   0.546, time=   0.0
gen=     270, best_score=   3.000, mean_score=   2.628, mean_gap=   0.372, time=   0.1
_______________________________________ result _______________________________________
para = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1])
score = 3.0
________________________________________ end _________________________________________

オール１が求まりました。

なお、N＝60は約７秒で、N＝300は約３分で大域解が求まりました↓。

________________________________________ info ________________________________________
para_range     : n=300
score_func     : <class 'function'>
aim            : ==100.0
show_pool_func : 'print'
seed           : None
pool_num       : 3000
max_gen        : None
core_num       : 1 (*vcopt, vc-grendel)
_______________________________________ start ________________________________________
Scoring first gen 3000/3000        
gen=       0, best_score=  43.740, mean_score=  33.111, mean_gap=  66.889, time=   4.3
gen=    3000, best_score=  45.470, mean_score=  35.844, mean_gap=  64.156, time=   6.7
gen=    6000, best_score=  46.780, mean_score=  37.882, mean_gap=  62.118, time=   9.1
gen=    9000, best_score=  48.450, mean_score=  39.635, mean_gap=  60.365, time=  11.4
・
・
・
・
gen=  210000, best_score=  99.330, mean_score=  96.842, mean_gap=   3.158, time= 167.0
gen=  213000, best_score=  99.660, mean_score=  97.164, mean_gap=   2.836, time= 169.4
gen=  216000, best_score=  99.660, mean_score=  97.453, mean_gap=   2.547, time= 171.8
gen=  219000, best_score= 100.000, mean_score=  97.746, mean_gap=   2.254, time= 174.2
_______________________________________ result _______________________________________
para = np.array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
score = 100.0
________________________________________ end _________________________________________

まとめ

3-Deceptive問題は変数間依存性が隣同士にしかありませんので、GAの一点交叉や二点交叉と相性が良さそうです。では離れた遺伝子座との依存性（もつれ）がある場合はどうでしょうか？一様交叉の方が有利になるでしょうか？また、３変数より多くの変数間にもつれている場合はどうでしょうか？（→NKランドスケープ問題を全探索と遺伝的アルゴリズムで解く）。点数の溝がより浅い場合は？深い場合は？・・・

組合せ最適化はまだまだ奥が深いようです。