本記事の内容は2019年5月13日に更新されました。
やること
実数値GAの難関、Rastrigin関数を最適化します。これができれば、どんな実数値(連続値)の最適化問題も大丈夫でしょう。
実行環境
WinPython3.6をおすすめしています。
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
import
まずは、今回使うパッケージをインポートします。今回はmathも使います。
import math
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcoptRastrigin関数とは
非常に多くの局所解をもつ多峰性の関数です。最適化アルゴリズムのラスボス的存在。解空間の形状は以下をご参考ください。
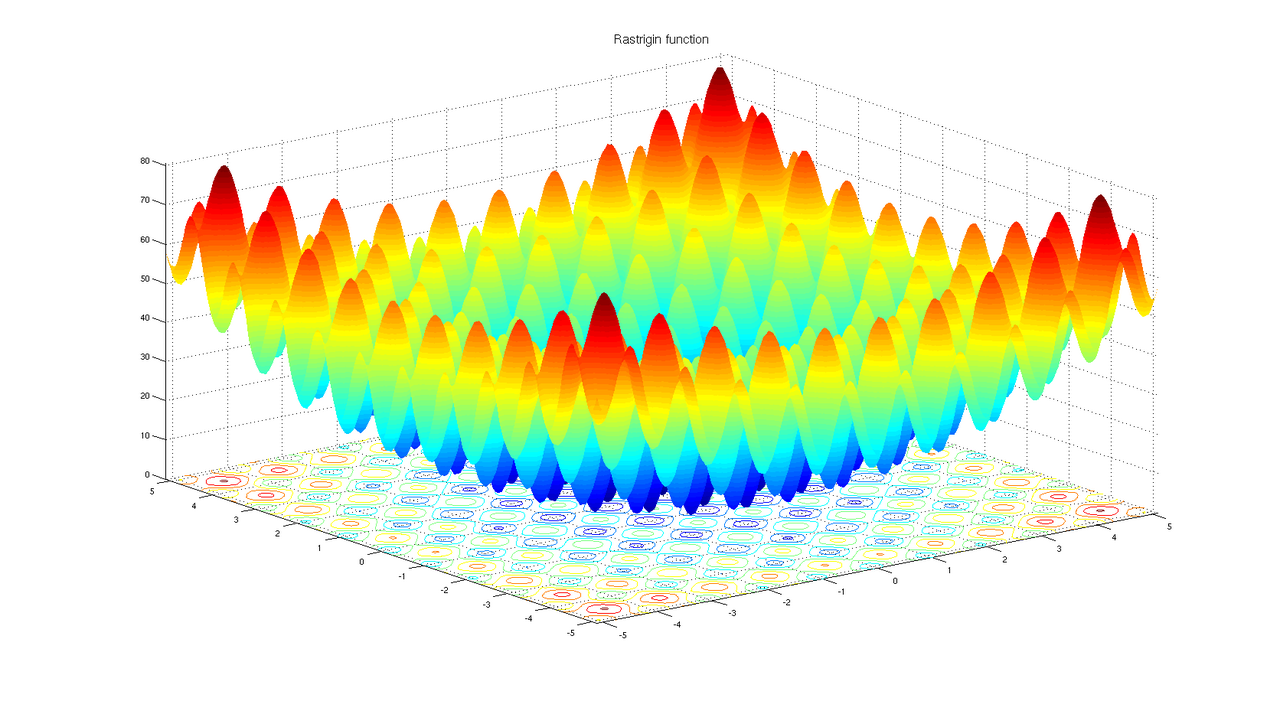
めっちゃギザギザしてます。便利なことに、何次元にも拡張して使えます。
1変数のRastrigin関数(=パラメータが1個(x)のとき)はこちら。xは-5.12~+5.12の範囲を取り得ます。
f = 10 + (x^2 - 10*cos(2πx))2変数のRastrigin関数(=パラメータが2個(x, y)のとき)はこちら。(x, y)はそれぞれ-5.12~+5.12の範囲を取り得ます。
f = 10 + (x^2 - 10*cos(2πx)) + 10 + (y^2 - 10*cos(2πy))n変数のRastrigin関数では、同様にパラメータの分だけ足してやれば良いです。n個のパラメータはそれぞれ-5.12~+5.12の範囲を取り得ます。
#Rastrigin関数(評価関数)
def rastrigin_score(para):
k = 0
for x in para:
k += 10 + (x*x - 10 * math.cos(2*math.pi*x))
return kこれを評価関数とします。
大域解
すべてのパラメータが0のとき、Rastrigin関数は最低値0を返します。
(任意)すべてのパラメータ群を可視化する関数
poolを受け取って、次元ごとに集団のパラメータをプロットします。
#poolの可視化
def rastrigin_show_pool(pool, **info):
#GA中の諸情報はinfoという辞書に格納されて渡されます
#これらを受け取って使用することができます
gen = info['gen']
best_index = info['best_index']
best_score = info['best_score']
mean_score = info['mean_score']
mean_gap = info['mean_gap']
time = info['time']
#プロット
plt.figure(figsize=(6, 6))
#次元の数だけ横線を引く
for dim in range(len(pool[0])):
plt.plot([-5, 5], [dim, dim], 'k-')
#poolを次元ごとに100個まで薄い黒でプロット
for dim in range(len(pool[0])):
plt.plot(pool[:100, dim], [dim]*len(pool[:100]), 'ok', markersize=8, alpha=(2.0/len(pool[:100])))
#エリートは赤でプロット
plt.plot(pool[best_index, :], range(len(pool[0])), 'or', markersize=8)
#タイトルをつけて表示
plt.xlabel('para'); plt.ylabel('dim')
plt.title('gen={}, best={} mean={} time={}'.format(gen, best_score, mean_score, time))
#plt.savefig('save/{}.png'.format(gen_num))
plt.show()
print()GAで最適化
実数値のGA(連続的なGA)はvcopt().rcGA()で実行します。まずは5次元のパラメータでやってみましょう。
#パラメータ範囲
para_range = np.ones((5, 2)) * 5.12
para_range[:, 0] *= -1
print(para_range)
#GAで最適化
para, score = vcopt().rcGA(para_range, #para_range
rastrigin_score, #score_func
0.0, #aim
show_pool_func=rastrigin_show_pool, #show_para_func=None
seed=None) #seed=None
#結果の表示
print(para)
print(score)実行結果
[[-5.12 5.12]
[-5.12 5.12]
[-5.12 5.12]
[-5.12 5.12]
[-5.12 5.12]]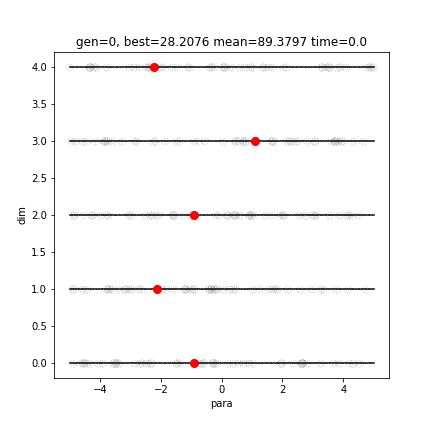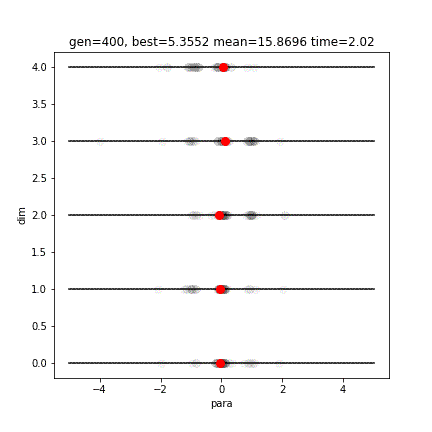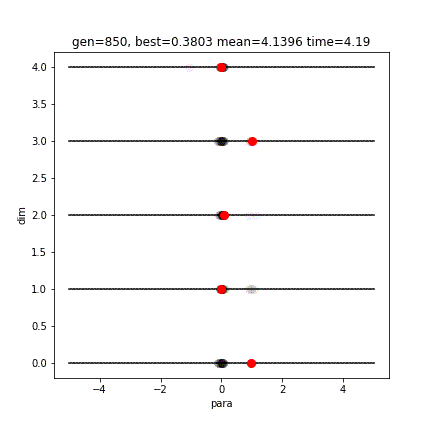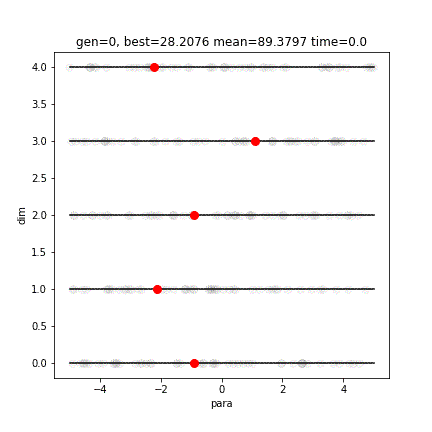
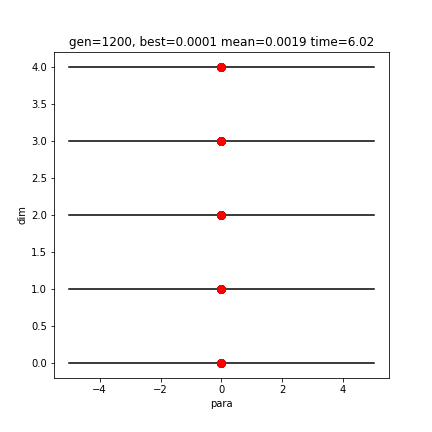
[ 0.00028274 0.00031257 0.00045897 -0.00018493 -0.00026573]
9.782879609154804e-05縦軸が次元です。5つのパラメータがすべて0付近となり、最適解は限りなく0に近い値です。vcopt().rcGA()では、計算効率を優先し、ほどほどの精度で計算を止めています。より厳密な解(0.0000000000000000000)に近づけたい場合は、続きから最急降下法などで頑張ってください。(2019/03/24現在、そこまでの実装を検討中です)
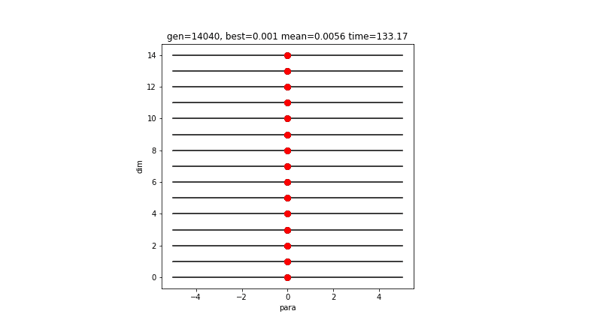
15次元
15次元でやってみましょう。
#パラメータ範囲
para_range = np.ones((15, 2)) * 5.12
para_range[:, 0] *= -1
#GAで最適化
para, score = vcopt().rcGA(para_range, #para_range
rastrigin_score, #score_func
0.0, #aim
show_pool_func=rastrigin_show_pool, #show_para_func=None
seed=None) #seed=None
#結果の表示
print(para)
print(score)実行結果

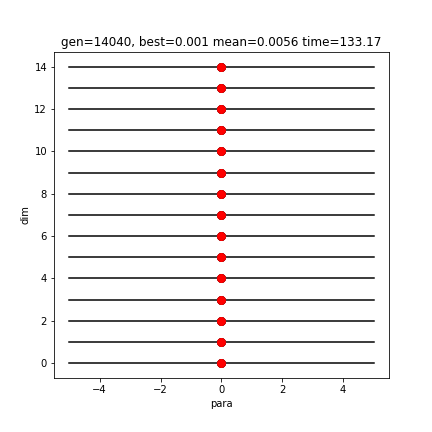
[-0.00019 0.00007974 0.00025465 -0.00047748 -0.00066942 0.00006996 0.00010788 0.00132598 -0.00040485 -0.00018067 -0.00044289 -0.00009191 0.00004059 -0.00083162 0.00126541]
0.0010423107729771175多次元、多峰性に対する圧倒的な対応力。完璧に調整されています。
実問題において、Rasriginほどの多峰性をもつ問題はめったにありません。どんな問題が来てもvcoptがあれば対応できると思います。