やること
冬の大三角って、微妙に正三角形ではない感じがするんですよね。
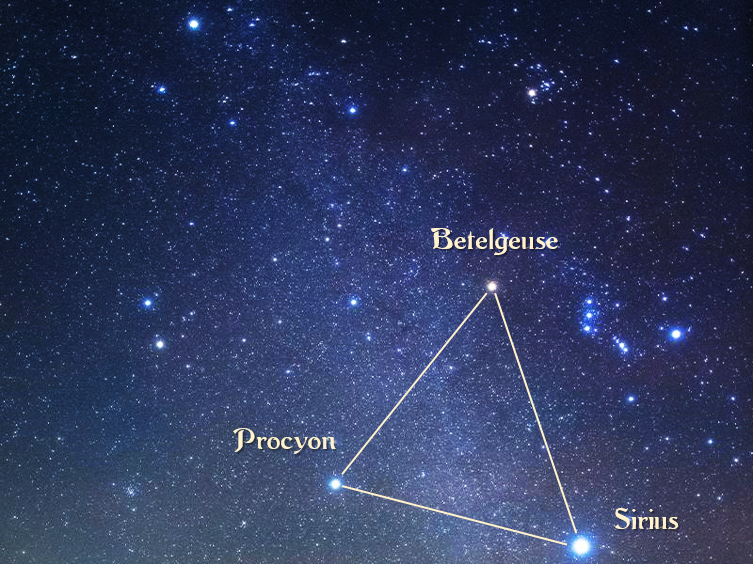
今回はvcoptで冬の大正三角を見つけてみます。
実行環境
WinPython3.6をおすすめしています。
Google Colaboratoryが利用可能です。

vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
サンプル画像
こちらのサイトから画像を拝借し、少し明るさを調整しました。謹んで感謝いたします。

調整後の画像です↓

pip, import
vcoptをインストールします。
pip install vcopt今回用いるパッケージをインポートします。
import cv2
import numpy as np
from vcopt import vcopt
from copy import deepcopy
import matplotlib.pyplot as plt画像の読み込みと明るい星の選別
画像を読み込んで、次の順に処理します。
- RGBへ変換(opencvのデフォルトはBGR読み込み)
- グレースケールへ変換
- 二値化(しきい値:128)
- オープニング処理(255領域を収縮した後に膨張させ、ごま塩ノイズを除去)
- 輪郭抽出
一定の明るさで選別された星の座標は、[よこ, たて]が並んだ2次元配列としてstars配列に格納されます。
#=============================
# パラメータ
#=============================
#画像パス
img_path = '9-17_sample.png'
#=============================
# 画像表示関数
#=============================
def show(img):
plt.figure(figsize=(10, 10))
plt.imshow(img, vmin = 0, vmax = 255)
plt.gray(); plt.show(); plt.close(); print()
#=============================
# 画像読み込みと輪郭抽出
#=============================
#画像読み込み
img = cv2.imread(img_path)
#show(img)
#BGR→RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
show(img)
#グレースケール
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#show(gray)
#二値化
_, binary = cv2.threshold(gray, 128, 255, cv2.THRESH_BINARY)
#show(binary)
#オープニング(ごま塩ノイズを除去)
kernel = np.ones((4, 4), dtype=np.uint8)
binary = cv2.morphologyEx(binary, cv2.MORPH_OPEN, kernel)
#show(binary)
#輪郭抽出
contours, _ = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
#すべての輪郭に線を引く
stars = []
for contour in contours:
x, y, w, h = cv2.boundingRect(contour)
star = (x + w//2, y + h//2)
size = (w + h)/4
#描画
cv2.circle(img, star, int(size), color=(255, 0, 0), thickness=2)
stars.append(star)
stars = np.array(stars)
print('len(stars):{}'.format(len(stars)))
show(img)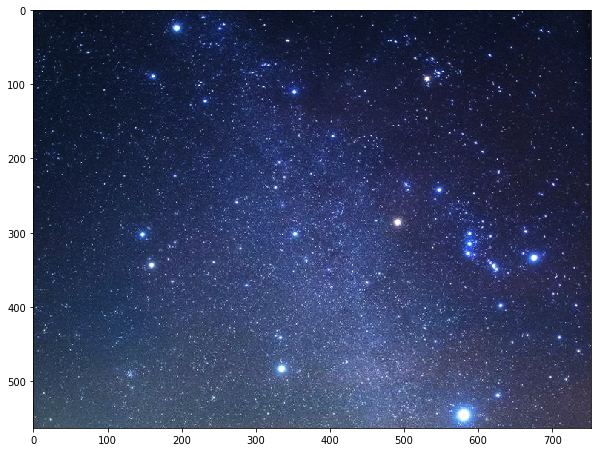
len(stars):23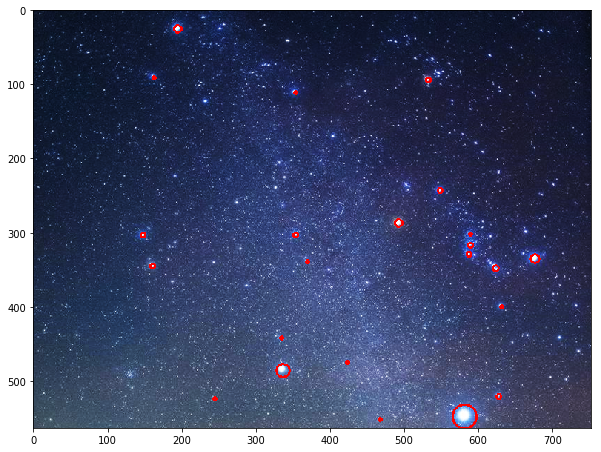
RGB変換後と輪郭抽出後に画像を出力しました。星は23個抽出されました。オリオン座もいます。気になる方は各段階でも画像を出力してみてください。
また、オープニング処理のカーネルサイズを小さくすると、より小さい星も残されます。
評価関数
遺伝子設計
遺伝子配列(para)は、0~22の範囲(=星ID)を取りうる3つの整数とします。これらの3つの星によって形成される三角形の辺の長さに注目します。
スコア設計
3辺の長さをその平均値で割って規格化し、3辺の分散値を求めて返します。分散値が小さいほど正三角形に近いですから、GAではスコア0.0を目指します。
visibleオプション
評価関数の2つ目の引数をTrueにすると、三角形が描画された画像が表示されるようにしておきました。
#=============================
# 評価関数
#=============================
def score_func(para, visible=False):
#paraに重複があれば1を返す
if len(set(para)) != len(para):
return 1
#3辺の長さ計算
length = np.zeros(len(para))
for i in range(len(para)):
length[i] = ((stars[para[i], 0] - stars[para[i-1], 0])**2 + (stars[para[i], 1] - stars[para[i-1], 1])**2)**0.5
#print(length)
#3辺の長さを規格化して分散をとる
variance = np.var(length / np.mean(length))
#オプションで情報表示、3辺を描画して表示
if visible:
print('length:{}'.format(length))
print('variance:{}'.format(variance))
img_copy = deepcopy(img)
for i in range(len(para)):
#cv2.drawMarker(img_save, tuple(stars[para[i]]), color=(0, 255, 0), markerType=cv2.MARKER_STAR, markerSize=10, thickness=1)
cv2.line(img_copy, (stars[para[i-1], 0], stars[para[i-1], 1]), (stars[para[i], 0], stars[para[i], 1]), (0, 255, 0), thickness=1)
show(img_copy)
#分散を評価値として返す
return variance
#冬の大三角のpara
para = np.array([1, 4, 17])
print('para:{}'.format(para))
#評価関数の確認
pscore_func(para, True)para:[ 1 4 17]
length:[275.75713953 252.7231687 252.85766747]
variance:0.0017280699018635845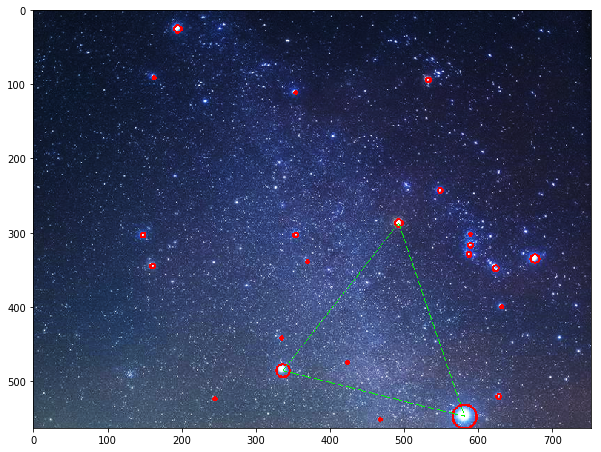
visibleオプションをTrueにして冬の大三角を表示してみました。3辺の長さは276, 253, 253で、分散は0.0017でした。二等辺三角形のようです。
GAで最適化
パラメータ範囲は、各遺伝子が取りうる範囲である[0, 1, 2, … , 22]が3個並んだ2次元配列です。離散値の最適化ができるvcopt().dcGA()を用いて最適化します。
最適化後にscore_func(para, True)で画像を確認します。
#=============================
# GAで最適化
#=============================
#パラメータ範囲
para_range = [[i for i in range(len(stars))] for j in range(3)]
#GAで最適化
para, score = vcopt().dcGA(para_range, #パラメータ範囲
score_func, #評価関数
0.0, #目標値
show_pool_func='print') #GA表示オプション
#結果の表示
score_func(para, True)___________________ info ___________________
para_range : n=3
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 30
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 30/30
gen=0, best_score=0.0191, mean_score=0.2642, mean_gap=0.2642, time=0.0
gen=30, best_score=0.0003, mean_score=0.0705, mean_gap=0.0705, time=0.0
gen=60, best_score=0.0003, mean_score=0.0478, mean_gap=0.0478, time=0.0
gen=90, best_score=0.0003, mean_score=0.0301, mean_gap=0.0301, time=0.0
・・・
gen=360, best_score=0.0001, mean_score=0.0042, mean_gap=0.0042, time=0.1
gen=390, best_score=0.0001, mean_score=0.0039, mean_gap=0.0039, time=0.2
gen=420, best_score=0.0001, mean_score=0.0029, mean_gap=0.0029, time=0.2
gen=450, best_score=0.0001, mean_score=0.0029, mean_gap=0.0029, time=0.2
__________________ results _________________
para : [20 8 15]
score : 6.898907043887647e-05
____________________ end ___________________
length:[275.17630712 269.80919184 273.72431386]
variance:6.898907043887647e-05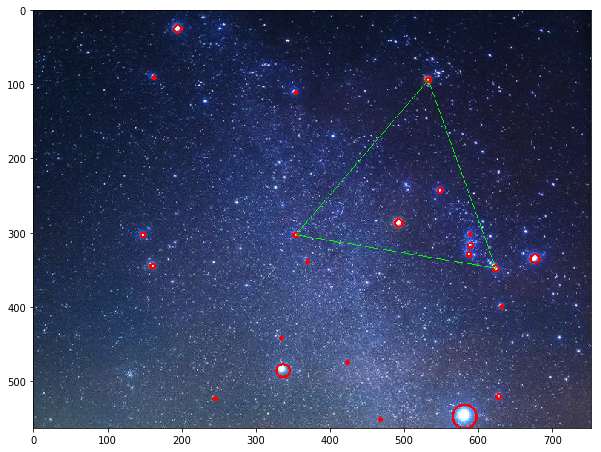
はい、大した組み合わせ数ではないので一瞬で終わりました。3辺が275, 270, 274の冬の大”正”三角です。
おまけ:冬の大正四角
正方形も見つけてしまおうと思い、評価関数を書き換えました。4つの辺の長さと、2つの対角線の長さをそれぞれ(1/√2)倍したもの、これら6つの長さの分散をとります。4辺だけだと正方形でない図形も対象になってしまうので、対角線で限定する必要があります。
#4辺と2本の対角線の長さ
length = np.zeros(len(para) + 2)
#4辺
for i in range(len(para)):
length[i] = ((stars[para[i], 0] - stars[para[i-1], 0])**2 + (stars[para[i], 1] - stars[para[i-1], 1])**2)**0.5
#2本の対角線
length[4] = ((stars[para[0], 0] - stars[para[2], 0])**2 + (stars[para[0], 1] - stars[para[2], 1])**2)**0.5
length[5] = ((stars[para[1], 0] - stars[para[3], 0])**2 + (stars[para[1], 1] - stars[para[3], 1])**2)**0.5
length[4:] /= 2**0.5
#print(length)パラメータ数も4つに増やし、GAの個体数も増やします。
#パラメータ範囲
para_range = [[i for i in range(len(stars))] for j in range(4)]
#GAで最適化
para, score = vcopt().dcGA(para_range, #パラメータ範囲
score_func, #評価関数
0.0, #目標値
show_pool_func='print', #GA表示オプション
pool_num=500) #個体数を増やす___________________ info ___________________
para_range : n=4
score_func : <class 'function'>
aim : 0.0
show_pool_func : 'print'
seed : None
pool_num : 100
max_gen : None
core_num : 1 (*vcopt, vc-grendel)
___________________ start __________________
Scoring first gen 100/100
gen=0, best_score=0.0197, mean_score=0.331, mean_gap=0.331, time=0.0
gen=100, best_score=0.0185, mean_score=0.1337, mean_gap=0.1337, time=0.1
gen=200, best_score=0.0185, mean_score=0.0993, mean_gap=0.0993, time=0.1
gen=300, best_score=0.0185, mean_score=0.0847, mean_gap=0.0847, time=0.2
・・・
gen=5400, best_score=0.0013, mean_score=0.0041, mean_gap=0.0041, time=1.8
gen=5500, best_score=0.0013, mean_score=0.004, mean_gap=0.004, time=1.8
gen=5600, best_score=0.0013, mean_score=0.0037, mean_gap=0.0037, time=1.8
gen=5700, best_score=0.0013, mean_score=0.0037, mean_gap=0.0037, time=1.9
__________________ results _________________
para : [ 3 11 17 5]
score : 0.0013304376005526225
____________________ end ___________________
length:[209.12197398 192.34604233 190.15782918 200.26232796 191.02486749
204.46148782]
variance:0.0013304376005526225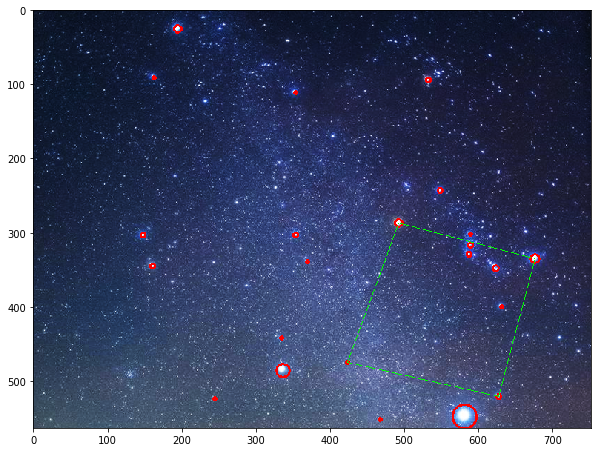
4辺が209, 192, 190, 200の四角形が見つかりました。選択肢が23個しかないせいか、ちょっと微妙ですね。
星を増やしたりして試しましたが、4点は少し歪むだけで正方形に見えなくなるようで、この画像内では厳しそうでした。



