本記事の内容は2019年5月13日に更新されました。
やること
巡回セールスマン問題をGAで最適化し、局所最適化手法である2-opt法の結果と比べてみましょう。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
import
まずは、今回使うパッケージをインポートします。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from vcopt import vcopt前回の関数をそのまま使う
巡回セールスマン問題の作成
#巡回セールスマン問題の作成
def create_tsp(town_num):
#町のx座標とy座標の配列を作成
town_x = nr.rand(town_num)
town_y = nr.rand(town_num)
return town_x, town_y(必須)評価関数
#巡回セールスマン問題の評価関数
def tsp_score(para):
#スコアの計算(今回は直接returnする)
return np.sum(((town_x[para][:-1] - town_x[para][1:])**2 + (town_y[para][:-1] - town_y[para][1:])**2)**0.5)(任意)すべてのパラメータ群を可視化する関数
さて、GAは複数の個体群(論文ではpopulationですが、ここではpoolと呼ぶことにします)を徐々に進化させながら最適化するアルゴリズムです。最適化の最中、複数の個体群がどんな感じか見たいですよね。
poolを可視化する関数にも、書き方のルールがあります。
#poolの可視化
def 関数名(pool, **info):
#GA中の諸情報はinfoという辞書に格納されて渡されます
#これらを受け取って使用することができます
gen = info['gen'] #現在の世代
best_index = info['best_index'] #エリート個体のインデックス
best_score = info['best_score'] #エリート個体の評価値
mean_score = info['mean_score'] #個体群の平均評価値
mean_score = info['mean_gap'] #目標値と評価値の差の絶対値平均
time = info['time'] #経過時間(秒)
#可視化
print(...)このルールに従い、pool可視化の関数をこのようにしました。
#巡回セールスマン問題のpoolの可視化
def tsp_show_pool(pool, **info):
#GA中の諸情報はinfoという辞書に格納されて渡されます
#これらを受け取って使用することができます
gen = info['gen']
best_index = info['best_index']
best_score = info['best_score']
mean_score = info['mean_score']
mean_gap = info['mean_gap']
time = info['time']
#プロット(および保存)
plt.figure(figsize=(6, 6))
#poolを100個まで薄い黒でプロット
for para in pool[:100]:
plt.plot(town_x[para], town_y[para], 'ok-', alpha=(2.0/len(pool[:100])))
#エリートは赤でプロット
plt.plot(town_x[pool[best_index]], town_y[pool[best_index]], 'or-')
#タイトルをつけて表示
plt.xlabel('x'); plt.ylabel('y')
plt.xlim([0, 1]); plt.ylim([0, 1])
plt.title('gen={}, best={} mean={} time={}'.format(gen, best_score, mean_score, time))
#plt.savefig('save/{}.png'.format(gen_num))
plt.show()
print()パラメータ数が20(←町の数)のとき、poolは200個体になりますが、すべてをプロットすると時間がかかるため、100個体を薄い黒で、最優秀個体(=エリート個体)を赤でプロットしています。この関数だけを実行するのはちょっと面倒なので、もうGAに入れちゃいましょう。エラーが出たらそのときに修正しましょう。(え)
GAで最適化
はじめに問題を作成し、その後GAを実行します。
#巡回セールスマン問題の作成
nr.seed(1)
town_num = 20
town_x, town_y = create_tsp(town_num)
#パラメータ範囲
para_range = np.arange(town_num)
#GAで最適化
para, score = vcopt().tspGA(para_range, #para_range
tsp_score, #score_func
0.0, #aim
show_pool_func=tsp_show_pool, #show_pool_func=None
seed=1) #seed=None
#結果の表示
print(para)
print(score)実行結果
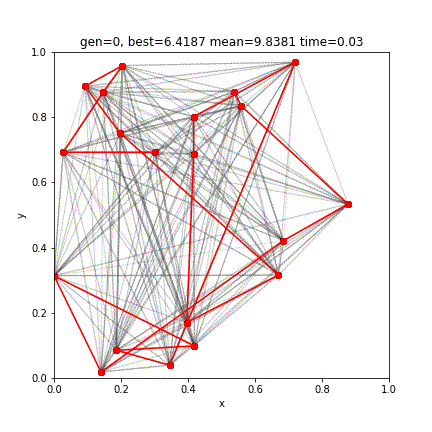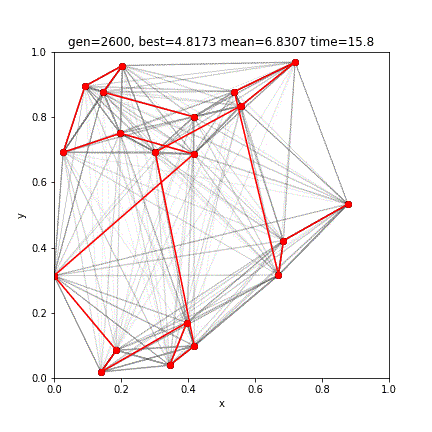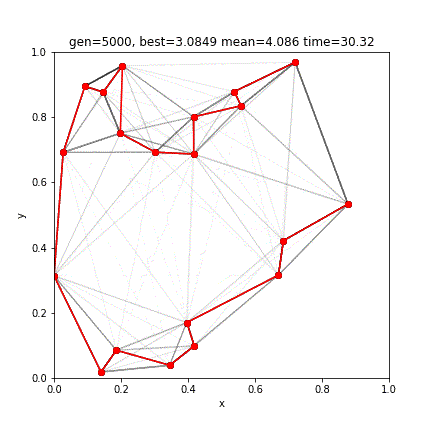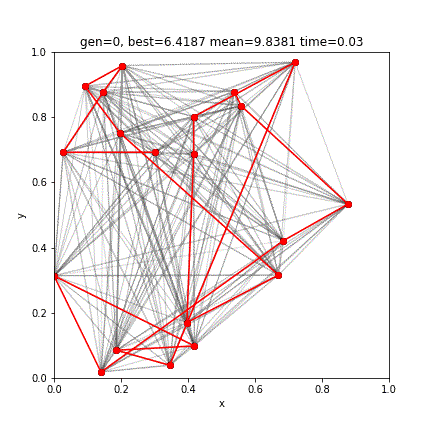
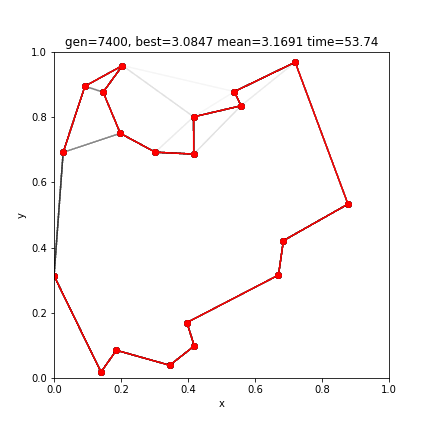
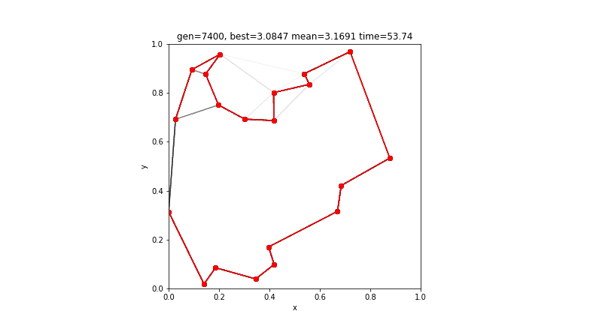
[ 1 9 17 0 16 3 19 4 12 5 14 2 18 6 7 10 8 15 11 13]
3.0847039502021065赤い線はエリート個体です。結果、4400世代の進化により、最短距離3.0847のルートが得られました。前回の2-opt法の結果と比べてみると、わずかに短いルートの発見に成功しています。
2-opt法(局所最適化)
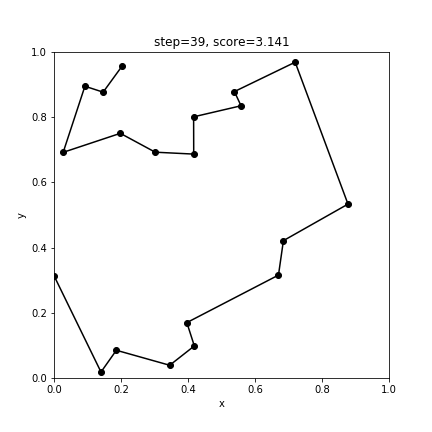
GA(大域最適化を目指す)