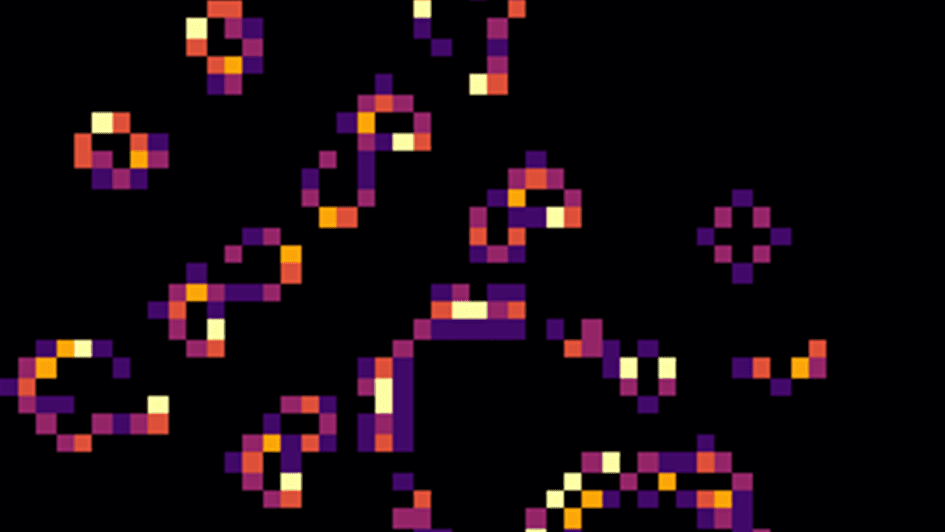やること
ライフゲームに年齢の概念を追加し、生き延びた時間に応じて色を付けてみましょう。
実行環境
WinPython3.6をおすすめしています。
WinPython - Browse /WinPython_3.6/3.6.7.0 at SourceForge.net
Portable Scientific Python 2/3 32/64bit Distribution for Windows
ライフゲームの基本
こちらの記事をご参照ください。
ソースコード
WinPython用のコードです。生セルの畳み込みはscipy.signal.convolve2d()を用いて一行で行い、フィールドはトーラス状にループさせています。また、plt.imshow()はデフォルトでは入力の最大値と最小値を取って規格化してしまうので、vmin, vmaxのオプションでこれを阻止します。bool配列とint配列を用いるので混乱しがち。
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from scipy import signal
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 10, 10
#任意の状態を用意
state = np.array([[0,0,1],
[1,0,1],
[0,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (0, 0)
#終了ステップ数
max_step = 79
#============================
#メイン処理
#============================
#フィールドの生成
f = np.zeros((h, w), dtype=int)
#任意の状態を置く
f[p[0]:p[0]+len(state), p[1]:p[1]+len(state[0])] = state
#畳み込み用のフィルタ
g = np.array([[1.0, 1.0, 1.0],
[1.0, 0.0, 1.0],
[1.0, 1.0, 1.0]])
#初期状態の表示
#plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='inferno', vmin = 0, vmax = 5)
#plt.savefig('save/{}.png'.format(0), bbox_inches='tight', pad_inches=0)
plt.show(), print()
#状態の更新
for i in range(1, max_step + 1):
#フィールドのbool版
f_bool = f > 0
#周囲の生存マス数をカウント
mask = signal.convolve2d(f_bool, g, mode='same', boundary='wrap')
#1ステップ未来のフィールド(すべて死状態)
future_bool = np.zeros(f.shape, dtype=bool)
#生きているマスが生きる条件(=生存)
future_bool[mask*f_bool==2] = 1
future_bool[mask*f_bool==3] = 1
#死んでいるマスが生きる条件(=誕生)
future_bool[mask*~f_bool==3] = 1
#futureの年齢版
future = np.array(future_bool, dtype=int)
#futureで生きているマスのうち、もともと生きていたところは年齢を足す
future[(future_bool==1) * (f_bool==1)] += f[(future_bool==1) * (f_bool==1)]
#フィールドの更新(浅いコピーに注意)
f = future
#表示
#plt.figure(figsize=(10, 10))
plt.imshow(f, cmap='inferno', vmin = 0, vmax = 5)
#plt.savefig('save/{}.png'.format(i), bbox_inches='tight', pad_inches=0)
plt.show(), print()
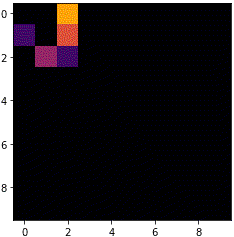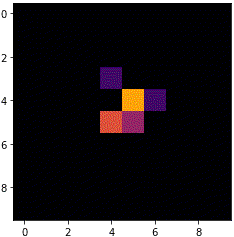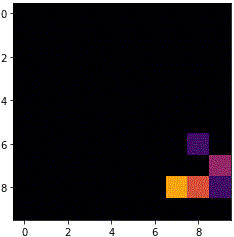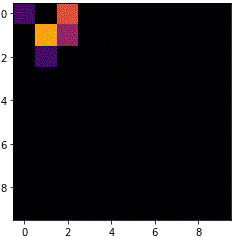
グライダーで実行してみる
ソースコードをそのまま実行すると、フィールドの左上からグライダーが進み始めます。
銀河
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 15, 15
#任意の状態を用意
state = np.array([[1,1,0,1,1,1,1,1,1],
[1,1,0,1,1,1,1,1,1],
[1,1,0,0,0,0,0,0,0],
[1,1,0,0,0,0,0,1,1],
[1,1,0,0,0,0,0,1,1],
[1,1,0,0,0,0,0,1,1],
[0,0,0,0,0,0,0,1,1],
[1,1,1,1,1,1,0,1,1],
[1,1,1,1,1,1,0,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (3, 3)
#終了ステップ数
max_step = 15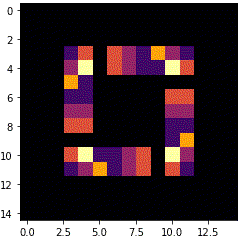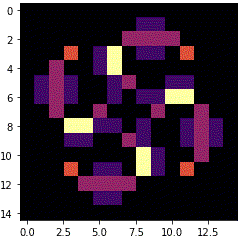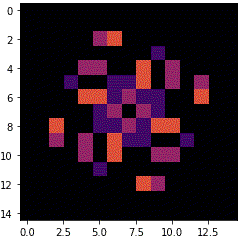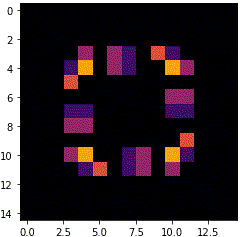
ダイハード
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 25, 25
#任意の状態を用意
state = np.array([[0,0,0,0,0,0,1,0],
[1,1,0,0,0,0,0,0],
[0,1,0,0,0,1,1,1]])
#フィールドのどこに置くか(左上点を指定)
p = (5, 9)
#終了ステップ数
max_step = 135十字スタート
#============================
#初期状態の設定
#============================
#高さ、幅
h, w = 281, 281
#任意の状態を用意
state = np.zeros((h, w))
state[140, :] = 1
state[:, 140] = 1
#フィールドのどこに置くか(左上点を指定)
p = (0, 0)
#終了ステップ数
max_step = 300plt.figure(figsize=(10, 10))